Las matemáticas del Juego del Solitario
septiembre 5, 2024
Mucho más que un pasatiempo: las matemáticas del Solitario
Por Miguel Barral.
El juego del Solitario habría sido inventado por un aristócrata francés durante su encierro en La Bastilla. Eso cuentan algunas versiones sobre su origen, que se situaría en la primera mitad del siglo XVII —pues esa fue la época en la que el monarca Luis XIV empleó la fortaleza como prisión para los nobles que no le eran afines. Sea más o menos creíble, este legendario origen pone de manifiesto tanto la antigüedad como la naturaleza del juego: un pasatiempo sencillo, que se puede jugar en cualquier sitio y que permite matar las horas en soledad; y de ahí su atemporal popularidad y vigencia.

Pero no ha sido hasta finales de 2019, cuando por fin se ha logrado determinar la probabilidad de ganar una partida. Esta cuestión, que durante décadas había sido objeto de estudio por parte de aficionados y matemáticos, se ha resuelto recurriendo a un programa informático para poder abordar los complejos y laboriosos cálculos.
Al margen de historias y leyendas, la primera referencia documentada sobre el juego corresponde a un grabado francés que representa a Anne-Joulie de Rohan-Chabot (1648-1709), princesa de Soubise, jugando al solitario. Esto sustentaría otra versión diferente sobre su origen, que identifica al matemático francés Pelisson como su inventor para entretenimiento de Luis XIV, conocido como el Rey Sol. Sin embargo, tal y como se refleja en el grabado, el juego representado es una modalidad del Solitario conocida como Solitario Noble o del Noble (y en inglés como Peg Solitaire) que se juega sobre un tablero con clavijas; y que atendiendo a ello podría ser el precursor u origen del juego de cartas.
Pasatiempo 1:
El Solitario (del) noble se juega sobre un tablero, que en su versión más habitual tiene forma de cruz y 33 agujeros, con el central vacío y los restantes ocupados por piezas o clavijas. El objetivo es que solo quede una pieza ocupando la posición central.
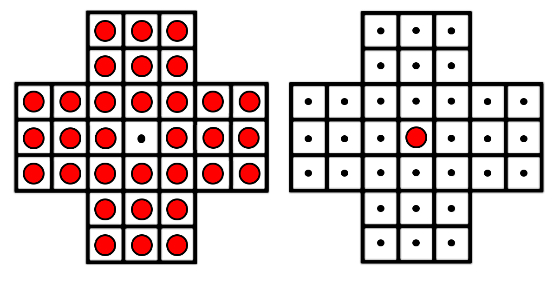
Para ello, el jugador debe ir eliminando clavijas una a una a base de saltar con una de ellas sobre otra —en horizontal o vertical— para ocupar un hueco libre. Tal que así:

A continuación se presentan dos configuraciones iniciales más sencillas. El reto es alcanzar el objetivo de que solo quede una clavija en la posición central:

nbsp;
EL SOLITARIO CON CARTAS
La modalidad jugada con cartas, que a la postre es la que ha acabado identificándose como Solitario, habría surgido a finales del siglo XVIII en los países bálticos como una forma de adivinación de la fortuna. Una hipótesis sustentada por el auge que en esa misma época experimentó la cartomancia y por el hecho de que en Escandinavia el juego era denominado Cabale, término que se ha vinculado a la Cábala judía.
Desde allí se habría extendido rápidamente al resto de Europa, tal y como atestigua que la primera referencia al término en el Oxford English Dictionary data de 1801. También que la primera obra conocida sobre el Solitario (una colección de juegos) apareciese publicada en Rusia en 1826; a la que poco después seguirían otras en Alemania y Francia. El juego se volvió tan popular que ya en sus Grandes Esperanzas (1864), Charles Dickens presenta a uno de los personajes jugando al Solitario.
Pasatiempo 2:
“Adivina” cuál es la carta que falta

Casi desde el mismo momento en que se popularizó, el Solitario concitó la atención de los matemáticos, que apoyados en la reciente rama de la Teoría de Juegos, trataron de determinar, entre otras cuestiones, la probabilidad de ganar una partida. Un cálculo que se les ha resistido desde entonces y que ha llegado a ser calificado como uno de los problemas más desconcertantes de las matemáticas.
Pasatiempo 3:
El Solitario danés es un juego o pasatiempo matemático en el que hay que colocar los naipes con valores del 1 al 10 en esta disposición:
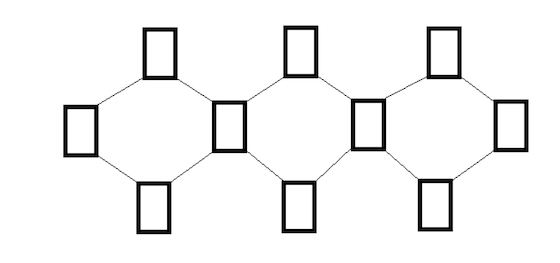
De tal modo que la suma de los cuatro naipes que conforman cada rombo y la suma de los cuatro naipes dispuestos en la fila central sea igual a 20, a 21, a 22, a 23 y a 24. ¿Cómo hay que colocarlos para que sumen 20 y 22?
EL PROGRAMA MÁS UTILIZADO DE MICROSOFT
A finales del s. XX el Solitario experimentó un nuevo e inesperado impulso con la aparición de los ordenadores personales. Y gracias en gran medida a Microsoft, que decidió incorporar el juego —en concreto, la modalidad conocida como Klondike— en el sistema operativo Windows 3.0 argumentando que se trataba de una forma amena e intuitiva de que el nuevo usuario se familiarizase con el manejo del ratón y de la interfaz gráfica. Desde entonces, no solo lo ha mantenido en todas las versiones posteriores de Windows, sino que ha introducido nuevas modalidades de juego en lo que constituye una apuesta segura ya que, según Microsoft, el Solitario es el más utilizado de sus programas, por delante incluso del Word y del Excel.
Ese “factor Microsoft” justifica que en el s. XXI el Klondike se haya convertido, con mucho, en la modalidad del Solitario más extendida y jugada. Y precisamente ha tenido que ser con el empleo de ordenadores (y en concreto con un programa de Inteligencia Artificial bautizado como Solvitaire) que se ha conseguido, por fin, establecer la probabilidad de ganar una partida para 45 modalidades diferentes del juego. Entre ellas, el Klondike, para el que el porcentaje de éxito se cifra en 81,96% ¿Será esta alta probabilidad de ganar otra de las claves de la popularidad del juego?
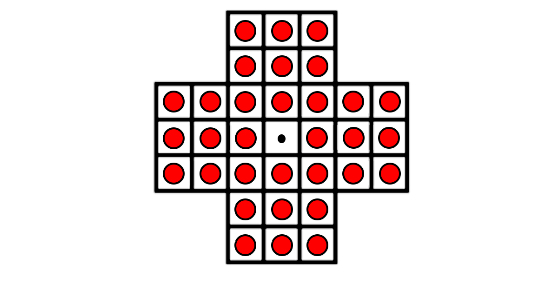
Pasatiempo 4
¿Una última partida al Solitario Noble? Como no podía ser de otra forma, ahora el reto es resolver la disposición usual, con 32 clavijas:


Pasatiempo 1:
Numerando las 33 posiciones del tablero de esta forma:

La solución para la configuración 1 es: 10-24, 15-17, 24-10, 19-17, 10-24.
Y para la 2: 10-02, 24-10, 19-17, 17- 05, 02-10, 15-17, 10-24, 29-17.
Pasatiempo 2:

El 3 de tréboles. En todas las filas la suma de las cartas impares es igual a la suma de las cartas pares. Y en cada fila se alinea una carta de cada palo.
Pasatiempo 3:
Pasatiempo 4:
Existen diversas soluciones, una de ellas es ésta:
05-17, 08-10, 01-09, 03-01, 16-04, 01-09, 28-16, 21-23, 07-21, 24-22, 21-23,26-24, 33-25, 31-33, 18-30, 33-25, 06-18, 13-11, 27-13, 10-12, 13-11, 24-26- 12-10, 10-08, 08-22, 22-24, 17-15, 29-17, 18-16, 15-17.
Miguel Barral está en Twitter (X): @migbarral
Fuente: bbvaopenmind.com
.
.
Teoría de los juegos en las medidas de Moreno
marzo 27, 2012
Teoría de los juegos en las medidas de Moreno
Por Sebastián Campanario
Ireversible” es una película francesa de 2002, dirigida por el argentino Gaspar Noé, que cobró celebridad por lo explícito de sus escenas de violencia. El título también le sienta bien a un debate de moda entre los economistas locales, en el que se intenta definir cuán “pasajeras” o “irreversibles” son las medidas de política económica adoptadas por el Gobierno en los últimos cuatro meses, de un mayor control del mercado cambiario y de las importaciones.
Buena parte de los economistas que defienden las decisiones aplicadas desde diciembre por Guillermo Moreno utilizan el siguiente argumento: “Las medidas de proteccionismo y de control cambiario no son aconsejables a priori, pero en un contexto de escasez de dólares pueden estar justificadas. De hecho, se frenó la fuga de capitales”.
Para Lucas Llach, profesor de la Di Tella y autor del blog “La ciencia maldita”, esta idea presenta un error conceptual: la actual dinámica está encerrada en un círculo vicioso que la hace muy difícil de revertir a futuro. “Si a un empresario se le da una señal para que produzca para sustituir importaciones, a futuro esa misma persona va a exigir que se cierre más la economía”, explica, “no es tan fácil volver atrás”.
El esquema que describe Llach se parece -salvando las distancias entre dos macroeconomías muy distintas- al que en su momento plantearon los economistas Daniel Heymann, Mariano Tomassi y Sebastián Galiani con la Convertibilidad y la teoría de los juegos, en una de las más elegantes estilizaciones propuestas para explicar la década del 90. En ese modelo se advertía una dinámica que se auto-profundizaba, y en la que los “costos de salida” son cada vez más elevados. Cada vez que surgían dudas con la caja de conversión y alguien sugería flexibilizarla, la respuesta del sistema era hacerse más rígido, con leyes de intangibilidad de depósitos, una nueva convocatoria a Domingo Cavallo, etc.
Los economistas que están viendo con preocupación este modelo advierten un sesgo anticrecimiento. Juan Llach, ex ministro de la Alianza y padre de Lucas, fue uno de los primeros en remarcar, el año pasado, este “cambio de regimen” con respecto a la economía de la primera etapa kirchnerista. Apreciación cambiaria, inflación elevada, deterioro fiscal, controles y proteccionismo son diferencias en variables centrales con respecto al período 2002-2007.
De otro lado, los optimistas -que son minoría entre los economistas-, subrayan que el actual es el Gobierno con mayor poder político de la historia, y por lo tanto con margen de maniobra para corregir sobre la marcha si se complica mucho el nivel de actividad.
A Lucas Llach, que tiene un doctorado en Historia en EE.UU., esta saga le hace acordar al segundo gobierno de Perón, con una economía más cerrada, menor crecimiento y conflictos distributivos. “El año clave que hay que mirar es 1959”, argumenta. Fue cuando Frondizi decidió liberar las tensiones acumuladas para atraer capitales del exterior, y la inflación, en una primera etapa, superó el 100%. Una película, por entonces, tan cruda como la de Gaspar Noé.
Fuente: Clarín, 26/03/12.
———————————
Teoría de Juegos
La teoría de juegos es un área de la matemática aplicada que utiliza modelos para estudiar interacciones en estructuras formalizadas de incentivos (los llamados «juegos») y llevar a cabo procesos de decisión. Sus investigadores estudian las estrategias óptimas así como el comportamiento previsto y observado de individuos en juegos. Tipos de interacción aparentemente distintos pueden, en realidad, presentar estructura de incentivo similar y, por lo tanto, se puede representar mil veces conjuntamente un mismo juego.
Desarrollada en sus comienzos como una herramienta para entender el comportamiento de la economía, la teoría de juegos se usa actualmente en muchos campos, como en la biología, sociología, psicología y filosofía. Experimentó un crecimiento sustancial y se formalizó por primera vez a partir de los trabajos de John von Neumann y Oskar Morgenstern, antes y durante la Guerra Fría, debido sobre todo a su aplicación a la estrategia militar, en particular a causa del concepto de destrucción mutua garantizada. Desde los setenta, la teoría de juegos se ha aplicado a la conducta animal, incluyendo el desarrollo de las especies por la selección natural. A raíz de juegos como el dilema del prisionero, en los que el egoísmo generalizado perjudica a los jugadores, la teoría de juegos ha atraído también la atención de los investigadores en informática, usándose en inteligencia artificial y cibernética.
Aunque tiene algunos puntos en común con la teoría de la decisión, la teoría de juegos estudia decisiones realizadas en entornos donde interaccionan. En otras palabras, estudia la elección de la conducta óptima cuando los costes y los beneficios de cada opción no están fijados de antemano, sino que dependen de las elecciones de otros individuos. Un ejemplo muy conocido de la aplicación de la teoría de juegos a la vida real es el dilema del prisionero, popularizado por el matemático Albert W. Tucker, el cual tiene muchas implicaciones para comprender la naturaleza de la cooperación humana. La teoría psicológica de juegos, que se arraiga en la escuela psicoanalítica del análisis transaccional, es enteramente distinta.
Los analistas de juegos utilizan asiduamente otras áreas de la matemática, en particular las probabilidades, las estadísticas y la programación lineal, en conjunto con la teoría de juegos. Además de su interés académico, la teoría de juegos ha recibido la atención de la cultura popular. La vida del matemático teórico John Forbes Nash, desarrollador del Equilibrio de Nash y que recibió un premio Nobel, fue el tema de la biografía escrita por Sylvia Nasar, Una mente brillante (1998), y de la película del mismo nombre (2001). Varios programas de televisión han explorado situaciones de teoría de juegos, como el concurso de la televisión de Cataluña (TV3) Sis a traïció (Seis a traición), el programa de la televisión estadounidense Friend or foe? (¿Amigo o enemigo?) y, hasta cierto punto, el concurso Supervivientes.
Aplicaciones
La teoría de juegos tiene la característica de ser un área en que la sustancia subyacente es principalmente una categoría de matemáticas aplicadas, pero la mayoría de la investigación fundamental es desempeñada por especialistas en otras áreas. En algunas universidades se enseña y se investiga casi exclusivamente fuera del departamento de matemática.
Esta teoría tiene aplicaciones en numerosas áreas, entre las cuales caben destacar las ciencias económicas, la biología evolutiva, la psicología, las ciencias políticas, el diseño industrial, la investigación operativa, la informática y la estrategia militar.
Economía y negocios
Los economistas han usado la teoría de juegos para analizar un amplio abanico de problemas económicos, incluyendo subastas, duopolios, oligopolios, la formación de redes sociales, y sistemas de votaciones. Estas investigaciones normalmente están enfocadas a conjuntos particulares de estrategias conocidos como conceptos de solución. Estos conceptos de solución están basados normalmente en lo requerido por las normas de racionalidad perfecta. El más famoso es el equilibrio de Nash. Un conjunto de estrategias es un equilibrio de Nash si cada una representa la mejor respuesta a otras estrategias. De esta forma, si todos los jugadores están aplicando las estrategias en un equilibrio de Nash, no tienen ningún incentivo para cambiar de conducta, pues su estrategia es la mejor que pueden aplicar dadas las estrategias de los demás.
Las recompensas de los juegos normalmente representan la utilidad de los jugadores individuales. A menudo las recompensas representan dinero, que se presume corresponden a la utilidad de un individuo. Esta presunción, sin embargo, puede no ser correcta.
Un documento de teoría de juegos en economía empieza presentando un juego que es una abstracción de una situación económica particular. Se eligen una o más soluciones, y el autor demuestra qué conjunto de estrategias corresponden al equilibrio en el juego presentado. Los economistas y profesores de escuelas de negocios sugieren dos usos principales.
Fuente: Wikipedia.



