Criptografía de Clave pública
abril 27, 2019 · Imprimir este artículo
50 años de secretos: la era de la criptografía moderna
Por Josu Sangroniz.
Tres personas que no se conocen, Ander, Blanca y Eva, se encuentran aisladas en una habitación. Blanca necesita saber la edad de Ander, que Eva no debe conocer bajo ningún concepto. ¿Hay alguna forma de que Ander pueda responder a Blanca sin revelar la información a Eva? Todo lo que cada uno diga o haga lo escucharán o verán los otros dos.
El sentido común dice que no: Blanca y Eva ven y oyen exactamente lo mismo, si en un momento dado una de ellas tiene información suficiente para deducir la edad de Ander, la otra la tendrá igualmente. Este problema, de haberse planteado hace cincuenta años, habría tenido seguramente la misma respuesta escéptica, sin embargo, en aquella época las cosas estaban cambiando.
Comenzaba una revolución, silenciosa para el ciudadano de a pie, cuyas consecuencias pocos podían prever. Se vivía el inicio de la revolución digital. Pesadas máquinas que llenaban habitaciones enteras eran capaces de efectuar cálculos y almacenar datos con una rapidez y un volumen desconocidos hasta entonces (que hoy nos haría sonreír) y poco a poco abandonaban los laboratorios de los centros de investigación para hacerse presentes en bancos y grandes industrias. Incluso con sus limitaciones, el manejo de grandes cantidades de datos trajo consigo nuevos retos a los que dar solución. Entre otros, establecer procedimientos para asegurar que la información se procesaba y transmitía libre de errores y protegerla de quien pudiera hacer uso malintencionado de ella.
No se puede decir que estos problemas fueran nuevos, pero sí lo era la escala de los potenciales afectados. En la era pre-digital la información que de verdad requería protección era relativamente poca, limitada esencialmente a ámbitos militares o de la burocracia gubernamental y en esos casos el coste que suponía mantener el nivel adecuado de seguridad era alto pero asumible.
La información es especialmente vulnerable mientras se transmite, antes o después de este momento su custodia no presenta grandes dificultades, pero ¿cómo puede protegerse mientras viaja a su destinatario por un canal que casi siempre escapa a nuestro control? La herramienta es el cifrado. En la era analógica, por llamar así a toda la historia de la humanidad salvo los aproximadamente últimos cincuenta años, la solución no dejaba de ser más o menos simple. Digamos que al espía o diplomático se le proveía de un “libro de claves” del que el receptor mantenía una copia.
En su versión más simple (pero también la más perfecta) un libro de claves no es más que una larguísima secuencia aleatoria de bits, es decir ceros y unos. Para cifrar un mensaje, que ya suponemos transcrito al lenguaje binario, el emisor suma simplemente los bits del mensaje, uno a uno, con los del libro empezando por el primero (emplea la suma binaria en la que 1+1=0). Así el mensaje cifrado resulta ser una cadena de bits tan aleatoria como la del libro y el enemigo que eventualmente capture el mensaje cifrado no tendrá absolutamente ninguna posibilidad de recuperar el mensaje original. Sin embargo, el receptor del mensaje, poseedor de una copia del libro de claves, no tiene ninguna dificultad puesto que si hace exactamente lo mismo que hizo el emisor descifrará el mensaje. Este es el esquema de la criptografia clásica, conocido y utilizado por la humanidad desde las civilizaciones más antiguas.
¿Pero por qué no sirve la criptografía clásica en el mundo digital? Pues porque exige algo que parece fácil a simple vista pero que en el mundo virtual es inviable por su coste: acordar cuál es el libro de claves. No es aceptable que cada vez que queramos comunicarnos con alguien, sea una persona de carne y hueso, una entidad bancaria, un comercio o una administración, estemos obligados a contactar previamente con ella, físicamente o mediante otro medio no digital, para establecer nuestra contraseña. Necesitamos hacerlo a través del mismo canal digital inseguro por el que se transmite toda la información. Estamos justamente enfrentados al problema de Ander, Blanca y Eva.
No está claro a quién atribuir la solución a este acertijo, sin la cual gran parte del mundo actual no podría funcionar. En 1976 los investigadores de la universidad de Stanford W. Diffie y M. Hellman publicaron un artículo que se considera el nacimiento oficial de la criptografía moderna, aunque, según parece, agencias de seguridad de algunos países ya habían desarrollado ideas similares poco antes. El fechar este suceso hace cincuenta años ha sido simplemente una pequeña licencia al hilo de la celebración del nacimiento de nuestra facultad.
Intentemos explicar en qué consiste eso de la criptografía moderna con un símil. Cifrar un mensaje no es más que meterlo en una caja que cerramos con un candado. En la criptografía clásica, como en la vida real, la “llave” que encripta y desencripta, esto es, la que cierra y abre el candado, es la misma, por eso no le sirve a Blanca, porque si le dice a Ander cómo tiene que encriptar, Eva, que está atenta, se da cuenta inmediatamente, no sólo de cómo encriptar, lo cual es inocuo, sino también, y esto es lo que queremos evitar a toda costa, de cómo desencriptar. Al dar la llave de cerrar a Ander, Blanca le está dando también la de abrir a Eva, puesto que es la misma (es decir, al dar la regla para encriptar a Ander le está dando sin querer la regla para desencriptar a Eva).
Lo que los descubridores (o inventores, cada cual que elija el término que considere más adecuado) de la criptografía moderna plantearon es que todo sería muy distinto si hubiera dos llaves diferentes, una para cerrar y otra para abrir. Entonces no habría ningún problema, Blanca podría dar con total tranquilidad una copia de la llave de cerrar a Ander (y también a Eva o a cualquiera) pero sólo ella retendría la llave de abrir. Así Eva vería pasar ante sus ojos la caja cerrada pero no podría hacer nada porque la llave que tiene sólo sirve para cerrar, es inútil para abrir.
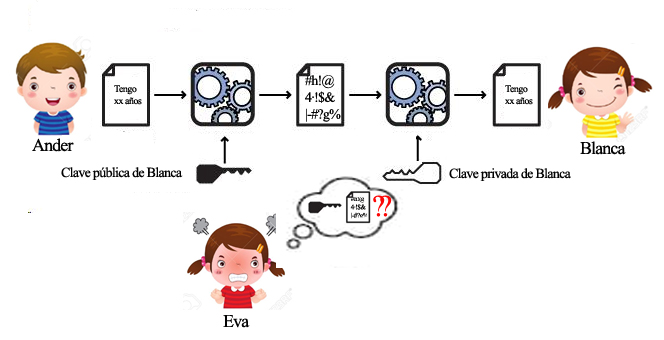
Lo anterior puede sonar convincente, pero sucede que las acciones de encriptar y desencriptar están inexorablemente ligadas, una no es más que el proceso inverso de la otra (como en el mundo real: cerramos girando la llave en un sentido y abrimos girándola en el sentido contrario). Sin embargo, es un hecho bastante común, al menos en el mundo matemático, que cuando dos procesos son inversos uno del otro, uno de ellos es mucho más costoso que su recíproco (así, es más difícil restar que sumar, dividir que multiplicar, extraer la raíz cuadrada que elevar al cuadrado… o recomponer los añicos de un jarrón chino que estrellarlo contra el suelo). Pero sucede que esto que nos protege de Eva, también afecta a Blanca, es decir para que nuestro esquema tenga sentido el proceso inverso (desencriptar) debe ser de una dificultad insuperable para Eva pero no para Blanca, que necesita saber cómo hacerlo para recuperar el mensaje original de Ander.
Las matemáticas están llenas de problemas difíciles, algunos con cientos o incluso miles de años de antigüedad, y que en ocasiones tienen enunciados arcanos sólo al alcance de iniciados. Afortunadamente éste no es el caso del que vamos a comentar ahora y que encaja en la tipología de los problemas inversos de los que hablábamos en el párrafo anterior. En la escuela todos aprendimos a multiplicar, primero los números de una cifra (un ejercicio de memorización) y luego los de dos o más. Ningún lector tendrá dificultad en realizar 17×71 o cualquier otra multiplicación que se quiera plantear, incluso aunque los factores tengan muchas más cifras. Es verdad que, si fueran dos números de, digamos, cien cifras, seguramente no tendríamos la paciencia suficiente para terminar (y, además, ¿qué interés puede haber en semejante operación?), sin embargo, con tiempo y motivación sería factible. Ni que decir tiene que un ordenador puede hacer este cálculo prácticamente al instante.
Lo interesante es ver qué pasa si lo intentamos al revés, es decir, si damos el resultado y el problema es encontrar dos números cuyo producto sea el indicado. Claro, si damos un número par es muy fácil. Pero ¿si damos 2021? (no hemos dado 2019 por razones obvias y tampoco 2017, por razones, quizá no tan obvias, que el lector sabrá adivinar). Pues no se me ocurre nada mejor que tantear: dividir entre 3, 5, 7, 11, 13, etc. (el lector reconocerá y entenderá por qué pruebo con estos números y no con 4, 6, 8, 9, 10, etc). Y sí, eventualmente encontramos que 2021=43×47. Pero, ¿y si en lugar de un número con 4 cifras damos uno con 100? La respuesta es que con un número bien elegido de 100 cifras hasta un potente ordenador tendría dificultades en encontrar su factorización, al menos en un tiempo razonable. Y si en lugar de 100 ponemos 200 ó 250 cifras podemos tener casi la certeza absoluta de que ni siquiera los grandes supercomputadores de las agencias de seguridad gubernamentales serían capaces de encontrar sus factores. Y que no piense el lector que el único método de factorización es la pura fuerza bruta de prueba y error como hemos podido dar a entender, pues en tal caso un número con sólo unas pocas decenas de cifras sería ya imposible de factorizar de esta manera. Se conocen algoritmos de factorización altamente sofisticados que utilizan matemáticas muy profundas, pero incluso estos algoritmos tienen limitaciones que, a día de hoy, hacen que podamos considerar imposible factorizar un número con 200 cifras.
Entonces ¿qué instrucciones da Blanca a Ander? Pues en primer lugar le proporciona dos números, digamos 2021 y 59; a continuación, le explica que calcule el resultado de elevar su edad a la potencia 59 y que cuando termine le diga el resultado. Hay un pequeño detalle: debe hacer las multiplicaciones de una manera un poco distinta a la habitual (y de hecho más simple): sólo debe considerar números de 0 a 2020, es decir debe tener en cuenta que a 2020 no le sigue 2021 sino ¡cero! y luego otra vez 1, etc. (por ejemplo, como 6561=3×2021+498, el número 6561 no es tal, sino 498). Con este procedimiento si la edad de Ander fuera 3 años (es sólo un ejemplo explicativo) calcularía
359 = ((((32)2)2)2)2×(((32)2)2)2×((32)2)2×32×3 = (65612)2×65612×6561×9×3
= (4982)2×4982×498×9×3 =…= 929.
Y éste sería el número que escucharíamos decir al pequeño (y superdotado) Ander. Sucede que Blanca sabe algo que, para dar verosimilitud a nuestra historia, suponemos nadie más conoce: la factorización 2021=43×47. Con los números 43, 47 y 59 y unas pocas matemáticas, que no tienen nada de secretas y se conocen bien desde hace más de 250 años, pero que por no abusar de la paciencia del lector no explicamos, Blanca calcula el número mágico 131, que es su clave secreta de descifrado. Y el milagro se produce: cuando Blanca eleva 929 a la potencia 131 y opera a la manera que antes hizo Ander, obtiene… ¡3! Eva, que sí conoce las matemáticas, pero no los factores 43 y 47, se ve incapaz de descubrir el número mágico 131 y por tanto se queda sin saber qué hacer con el número 929.
El sistema criptográfico que acabamos de explicar se llama RSA, es el primer sistema de clave pública que se descubrió y uno de los más utilizados desde entonces. La única diferencia es que obviamente no se emplean números como 43 y 47 sino números primos con 80 ó 100 cifras.
Así que finalmente Ander habla y dice: “Tengo 57 años”, a lo que Blanca responde, “Bonita edad. Además, es un número primo”.
Para saber más:
W. Diffie, M. E. Hellman (1976) “New Directions in Cryptography” IEE Transactions on Information Theory 22, no. 6, 644-654. Disponible como PDF aquí.
J. Sangroniz (2004) “Criptografía de clave pública: el sistema RSA” Sigma 25, 149-165. Disponible en como PDF aquí.
Sobre el autor: Josu Sangroniz es Profesor de Álgebra en el Departamento de Matemáticas de la Facultad de Ciencia y Tecnología de la UPV/EHU
Fuente: culturacientifica.com, 2019.

______________________________________________________________________________
Vincúlese a nuestras Redes Sociales:
LinkedIn YouTube Facebook Twitter
______________________________________________________________________________
.
.




[…] Criptografía de Clave pública […]