La magia del interés compuesto
agosto 27, 2015 · Imprimir este artículo
Invertir a largo plazo: La magia del interés compuesto
¿Quiere sacar el máximo partido a su dinero y beneficiarse de la magia del interés compuesto? Entonces, invierta cuanto antes…
 Quizá alguién le ha hecho ya la siguiente pregunta trampa: “¿Preferirías tener 1.000 euros cada día durante un mes, o un céntimo de euro que doblase su valor cada día durante un mes?” Hoy, sabemos que es mejor la segunda opción porque después de 30 días habríamos acumulado unos 5 millones de euros contra los 30.000 euros de la primera opción.
Quizá alguién le ha hecho ya la siguiente pregunta trampa: “¿Preferirías tener 1.000 euros cada día durante un mes, o un céntimo de euro que doblase su valor cada día durante un mes?” Hoy, sabemos que es mejor la segunda opción porque después de 30 días habríamos acumulado unos 5 millones de euros contra los 30.000 euros de la primera opción.¿Cómo funciona exactamente?
El principio es simple: invierta un euro durante un año, a un interés anual de, digamos el 10%, y su dinero valdrá 1,10 euros al final del año. Si sigue invirtiendo esos 1,10 euros durante otro año, con una rentabilidad del 10% sobre la cantidad total, acabará con 1,21 euros tras dos años. El primer año usted generó solo 10 céntimos, pero el segundo generó 11 céntimos de euros.
Ese es el beneficio del interés compuesto. Veamos ahora cómo puede ayudarnos en nuestro plan financiero de cada día.
Todos nosotros tenemos objetivos financieros de cara al futuro, como el que nos ocupa en esta sección que es preparar la jubilación.
Una de las consecuencias de lo que acabamos de explicar con el interés compuesto es que lo que todo el mundo repite constantemente y que es muy importante: cuanto antes empiece uno a ahorrar, o mejor dicho invertir, más probable será que uno consiga su objetivo.
¿Cuál será su estrategia de inversión?
Veamos un simple ejemplo de dos jóvenes de misma edad que aspiran a tener una jubilación dorada, llamémosles Paco y Guillermo. Los dos han hecho sus cálculos y les gustaría llegar a su jubilación con un millón de euros bajo el brazo (… ¿a quién no?).
Paco tomó la decisión de invertir cuanto antes. Empezó a hacerlo a los 24 años, invirtiendo una cantidad de unos 2.000 euros al año, hasta los 30 años. En ese periodo consiguió una rentabilidad del 12% neto, y a pesar de que dejó de ahorrar tras cumplir los 30, dejó el dinero invertido donde siguió ganando un 12% cada año hasta que se retiró a los 65.
Guillermo, por su parte, siguió gastándose su dinero durante unos 6 años, desde los 24, antes de que empezase a ahorrar (a los 30 años) los mismos 2.000 euros, también consiguiendo un 12% neto al año gracias. Sin embargo, Guillermo a contrario de Paco hizo el esfuerzo de invertir unos 2.000 euros cada año hasta que se retiró.
¿Quién consiguió 1 millón de euros para su jubilación?
¿Quién cree usted que consiguió el objetivo de tener 1 millón de euros en el momento de jubilares? Intuitivamente uno diría que el agraciado es Guillermo ya que hizo el esfuerzo de invertir 2.000 euros al año desde los 30 años hasta los 65 años. Pero, en realidad, los dos lograron el objetivo, pero con una diferencia importante.
Paco, porque empezó a ahorrar pronto, tuvo que invertir sólo 12.000 euros (2.000 euros durante 6 años), mientras que Guillermo tuvo que invertir 72.000 euros (2.000 euros durante 36 años), es decir 6 veces la cantidad que invirtió Paco para llegar al mismo sitio. Por lo tanto, esperar 6 años le costó a Guillermo 60.000 euros.
 La lección es que invertir pronto puede ser tan importante como la cantidad invertida durante toda una vida. Eso significa que para realmente beneficiarse de la magia del interés compuesto es importante empezar a invertir – o pagar sus deudas porque el mismo principio se aplica a la inversa – lo antes posible.
La lección es que invertir pronto puede ser tan importante como la cantidad invertida durante toda una vida. Eso significa que para realmente beneficiarse de la magia del interés compuesto es importante empezar a invertir – o pagar sus deudas porque el mismo principio se aplica a la inversa – lo antes posible.
La idea, prevalente entre mucha gente que planea su jubilación, de que lo que hagan mientras tienen 20 o 30 años no importa es una falacia. Recuerde, por este efecto del interés compuesto, que la rentabilidad genera rentabilidad. Esta es la verdadera magia del interés compuesto.
Fuente: www.morningstar.es, 16/07/15.
Interés compuesto
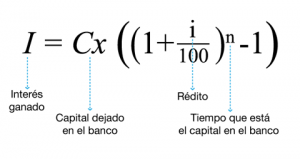
El interés compuesto representa la acumulación de intereses que se han generado en un período determinado por un capital inicial (CI) o principal a una tasa de interés (r) durante (n) periodos de imposición, de modo que los intereses que se obtienen al final de cada período de inversión no se retiran sino que se reinvierten o añaden al capital inicial, es decir, se capitalizan.
Cálculo del interés compuesto
Para un período de tiempo determinado, el capital publico (CF) se calcula mediante la fórmula
Ahora, capitalizando el valor obtenido en un segundo período
Repitiendo esto para un tercer período
y generalizando a n los períodos, se obtiene la fórmula de interés compuesto:
Donde:
 es el capital al final del enésimo período
es el capital al final del enésimo período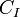 es el capital inicial
es el capital inicial es la tasa de interés expresada en tanto por uno (v.g., 4 % = 0,04)
es la tasa de interés expresada en tanto por uno (v.g., 4 % = 0,04) es el número de períodos
es el número de períodos
Para calcular la tasa de interés compuesto total se usa la fórmula:
Donde:
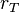 es la tasa de interés total expresada en tanto por uno (v.g., 1,85 = 185 %)
es la tasa de interés total expresada en tanto por uno (v.g., 1,85 = 185 %) es la tasa de interés expresada en tanto por uno (v.g., 4 % = 0,04)
es la tasa de interés expresada en tanto por uno (v.g., 4 % = 0,04) es el número de períodos
es el número de períodos
Para hacer cálculos continuos en el tiempo en lugar de calcular cantidades para finales de períodos puede usarse la tasa de interés instantánea  , así el capital final actualizado al tiempo t viene dado por:
, así el capital final actualizado al tiempo t viene dado por:
El resto de tasas pueden calcularse sin problemas a partir de la tasa de interés instantánea.
Obtención de los elementos de la fórmula de interés compuesto
De la ecuación del interés compuesto, para n períodos, se obtiene el capital inicial, conocidos el capital final, el interés y el número de períodos:
El número de períodos puede calcularse, conocidos los capitales inicial y final y el interés, despejando n en la última fórmula, obteniéndose:
El interés puede calcularse, conocidos los capitales inicial y final y el número de períodos, despejándolo de esa misma fórmula:
Fuente: Wikipedia, 2015.
.





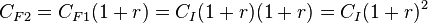

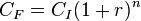


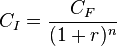

![r = \left( {\frac{C_F} {C_I}}\right)^{\frac{1} { n}}- 1= \sqrt[n]{\frac{C_F} {C_I} }- 1](https://upload.wikimedia.org/math/5/e/1/5e18417e6346aac505bcaf963c050be1.png)

Comentarios
Algo para decir?
Usted debe estar logueado para escribir un comentario.