El Teorema de Bayes en el Análisis de Inteligencia
julio 1, 2020
“Bayes ingenuo” en apoyo del análisis de inteligencia
Por José-Miguel Palacios.
Un interesante artículo de Juan Pablo Somiedo[1], aparecido a finales de 2018, nos recordaba que el teorema de Bayes[2], en su versión más elemental (lo que se suele llamar “Bayes ingenuo”) puede seguir siendo útil en análisis de inteligencia.
El teorema de Bayes en el análisis de inteligencia
Se puede argumentar que todo análisis de inteligencia es bayesiano en su naturaleza. En esencia consiste en obtener unas evidencias iniciales, simples fragmentos de una realidad bastante compleja, para formular después hipótesis explicativas, recolectar más evidencia y verificar cuál de nuestras hipótesis se ajusta mejor a la evidencia disponible. Algo que no es esencialmente distinto de la “lógica bayesiana”, es decir, de ir modificando nuestras valoraciones subjetivas iniciales a medida que vamos recibiendo evidencias más o menos consistentes con ellas.
En las décadas de 1960 y 1970 hubo varios intentos de utilizar directamente el teorema de Bayes para fines de análisis de inteligencia. Algunos de ellos han sido documentados en las publicaciones del Centro para el Estudio de la Inteligencia de la CIA[3]. Los resultados, sin embargo, no llegaron a ser plenamente convincentes. Y una de las razones principales fue que el mundo real resultó ser demasiado complejo para los modelos elementales que deben considerarse al utilizar “Bayes ingenuo”. Y es que estos modelos presuponen la invariabilidad de la situación inicial (oculta a nuestros ojos), así como la independencia absoluto de los sucesos que vamos considerando. Este problema puede resolverse mediante el uso de “redes bayesianas”[4] y los resultados son matemáticamente correctos, aunque aquí el principal problema radica en conseguir modelar correctamente la realidad. Es el enfoque que fue seleccionado para el programa Apollo[5] y otros similares.
A pesar de todo, y con las debidas precauciones, el uso de “Bayes ingenuo” puede ayudarnos en algunos casos a valorar la evidencia de que disponemos. Para que ello sea así, tendríamos que prestar atención a neutralizar las principales debilidades del método. A saber:
a) Deberíamos utilizar únicamente evidencia relativamente “reciente” (algo que, medido en tiempo, puede tener distintos significados dependiendo de los casos). El problema es que Bayes nos da información sobre una situación preexistente y oculta (por ejemplo, la decisión que puede haber adoptado un determinado líder político) fijando nuestra atención en sus manifestaciones visibles. Si la evolución de la situación es bastante lenta (por ejemplo, la soviética durante el brezhnevismo medio y tardío), podemos asumir que no cambia sustancialmente durante años, por lo que el momento de obtención es escasamente relevante para la valoración de la evidencia. En situaciones más dinámicas, como suelen ser la actuales, las posiciones de los líderes se están modificando continuamente como consecuencia de los cambios que se producen en el entorno. Evidencia relativamente antigua puede referirse a una “situación oculta” que ya no es actual. Por ello, deberíamos utilizar solo evidencia bastante nueva y, si la crisis continúa, prescindir de la más antigua en beneficio de otra más reciente.
b) En la medida de lo posible, el conjunto de las hipótesis debería cubrir la totalidad de las posibilidades existentes, y no debería existir ningún solape entre las diferentes hipótesis. En la práctica, este objetivo es casi imposible de alcanzar, aunque cuanto más nos acerquemos a él, más fiables serán los resultados que obtengamos al aplicar “Bayes ingenuo”.
c) Las evidencias (“Sucesos”) deberían ser de un “peso similar” y no estar relacionadas entre sí[6].

En la práctica
Hemos elaborado una hoja de Excel[7], con la esperanza de que pueda ayudar con los cálculos matemáticos que esta técnica requiere. Para rellenarla, seguiremos los siguiente pasos, sugeridos por Jessica McLaughlin[8]:
1) Creamos un conjunto de hipótesis mutuamente excluyentes y colectivamente exhaustivas relativas al fenómeno incierto que queremos investigar. Como ya hemos explicado, es, quizá, uno de los pasos más difíciles. En general, resulta complicado imaginar hipótesis que sean por completo mutuamente excluyentes (sin ningún solape entre ellas). Y no lo es menos conseguir que el conjunto de ellas agote todas las posibilidades.
2) Asignamos probabilidades previas (pr.previa, en nuestra hoja de cálculo) a cada una de las hipótesis. La probabilidad previa es nuestra estimación intuitiva de la probabilidad relativa de cada una de las hipótesis. Dado que son mutuamente excluyentes y que cubren todas las posibilidades, la suma de las probabilidades previas debe ser 1. En nuestra tabla, expresamos las probabilidades en tantos por ciento.
3) Ahora debemos ir incorporando los “Sucesos” que nos servirán para valorar las hipótesis. El método reajusta las probabilidades de las hipótesis después de cada suceso, por lo que estos pueden añadirse secuencialmente, según se van produciendo o según tenemos noticia de ellos. Una buena elección de sucesos es muy importante para que el método produzca resultados aceptables. Los sucesos deben tener valor diagnóstico (es decir, deben ser más o menos probables según cuál de las hipótesis es la correcta) y, en lo posible, de un “peso” (importancia) similar.
4) Según incorporamos “Sucesos” a la tabla, les asignamos “verosimilitudes” (“verosim.”, en nuestra hoja de cálculo), relativas a cada una de las hipótesis. Se trata para cada caso de la probabilidad estimada por el analista de que el suceso ocurra, suponiendo que la hipótesis que estamos considerando sea correcta. En la tabla, esta probabilidad la expresamos por un entero entre 0 y 100, siendo 0 la imposibilidad total, y 100 la seguridad completa (de que el suceso se producirá suponiendo que la hipótesis se verifica). Obviamente, la suma de todas las verosimilitudes no tiene por que ser la unidad (100% o, según la notación que utilizamos en nuestra tabla, 100).
La propia tabla recalculará las probabilidades de las hipótesis una vez que hayamos computado cada “Suceso”. En nuestra tabla, podemos encontrar estas probabilidades recalculadas en la columna G (“probab.”).
5) Reiteraremos el proceso según añadimos nuevos sucesos. En nuestra tabla, cada nuevo suceso está representado 10 filas más abajo del anterior. Si agotamos los predefinidos en la tabla, podemos añadir más copiando el último “bloque” diez filas más abajo.
Un ejemplo: Crisis de Crimea, marzo de 2020
El proceso puede verse mucho más claro con la ayuda de un ejemplo. Utilizaremos el de la crisis de Crimea de 2014, en particular las dos semanas que siguieron a la caída del Presidente ucraniano Yanukovich, el 21 de febrero. Hemos rellenado la hoja Excel con una serie de “Sucesos” y el resultado puede encontrarse en la hoja prueba_crimea.xlsx[9]. Se trata, evidentemente, de un supuesto didáctico en el que la elección su “Sucesos” y la determinación de las verosimilitudes están condicionados por el interés en ilustrar algunos de los posibles resultados.
Como vemos, la técnica nos permite calcular en todo momento las probabilidades de las diversas hipótesis, y mantener este cálculo actualizado según vamos recibiendo nueva información. Algunas observaciones interesantes:
- a) A fecha 6 de marzo de 2014, consideraríamos casi seguro (probabilidad del 90%) que la intención rusa sea anexionar la península de Crimea.
- b) Sin embargo, unos días antes (según la tabla) no estaría tan claro. El 1 de marzo la hipótesis de la anexión era ya la más probable (55%), pero aún calculábamos una probabilidad notable (39%) de que los rusos estuvieran intentando crear una república virtualmente independiente sin poner en cuestión (formalmente) las fronteras reconocidas (modelo “Transnistria”).
- c) Tan solo unos días antes, hacia el 25-26 de febrero, la hipótesis más probable era aún que los rusos estuvieran intentando impedir que el nuevo gobierno de Kiev tomara el control efectivo de Crimea (probabilidad del 63-68%).
Con la tabla, podemos fácilmente excluir como sospechoso de desinformación un suceso que hemos aceptado previamente, modificar la verosimilitud de sucesos pasados a la luz de nueva evidencia, o cambiar las probabilidades previas de las que hemos partido. En todos estos casos, la tabla nos recalcula automáticamente todas las probabilidades.
Bayes ingenuo y Análisis de Hipótesis Alternativas (ACH)
En el fondo, la técnica de Bayes ingenuo no es muy diferente del Análisis de Hipótesis Alternativas (ACH) de Heuers. La lógica subyacente es la misma (conocer una realidad oculta gracias al estudio de sus manifestaciones visibles) y la diferencia principal radica en la forma de atacar el problema: mientras Bayes ingenuo calcula las probabilidades relativas, ACH intenta descartar hipótesis por ser inconsistentes con la evidencia.
Para ilustrar mejor las diferencias entre estas dos técnicas, hemos elaborado una matriz (prueba ach_crimea.xlsx[10]) con los sucesos y las hipótesis del ejemplo sobre Crimea. Como sabemos, las diversas variantes de ACH se diferencian entre sí por la manera de contabilizar los resultados. En nuestro caso, marcaremos CC y contaremos 2 puntos cuando el suceso sea altamente consistente con la hipótesis, C (1 punto) cuando sea consistente, I (-1) cuando sea inconsistente y X (rechazo de la hipótesis) cuando sea incompatible. Con estas reglas, hemos llegado a los resultados que a continuación se indican:
a) La hipótesis de la Anexión parece la más probable, aunque seguimos atribuyendo una probabilidad considerable a la hipótesis del Caos. Las dos primeras hipótesis (Evitar el control de Kiev sobre la península y el modelo Transnistria) podrían ser descartadas.
b) Si elimináramos la última fila, es decir, si no tomáramos en consideración el suceso del 6 de marzo, las cuatro hipótesis seguirían siendo verosímiles, con dos de ellas (Anexión y Transnistria) vistas como claramente más probables.
Vemos, pues, que partiendo de una lógica similar, las dos técnicas nos conducen a resultados ligeramente distintos. Y en el proceso podemos apreciar algunos de los inconvenientes que cada una de ellas tiene:
a) En ACH el principal problema es que no siempre resulta fácil encontrar sucesos que desmientan alguna de las hipótesis (“coartadas”) por ser completamente incompatibles con ella. Y, en ocasiones, sucesos muy interesantes pueden ser sospechosos de desinformación.
b) En ausencia de “coartadas”, la puntuación en ACH depende mucho de la metodología de cálculo que se siga. La que hemos elegido es, quizá, excesivamente simple. Otras más complejas pueden resultar difíciles de aplicar (aunque hay programas informáticos que pueden servir de ayuda) y resultar en cierta medida arbitrarias.
c) El problema con Bayes ingenuo es que para muchos analistas no resulta intuitivo. El uso de la hoja Excel ayuda mucho a realizar los cálculos, pero puede oscurecer la lógica que hay detrás de ellos.
A modo de conclusión
a) El Teorema de Bayes no sirve para predecir el futuro, sino que nos ayuda a conocer una realidad pasada o presente que permanece oculta a nuestros ojos. Es obvio que si el Presidente del país X ha decidido invadir el país vecino Y, acabará haciéndolo, de no mediar alguna circunstancia que le haga cambiar de opinión. Pero lo que averiguamos no es el hecho futuro (que invadirá), sino el pasado (que ha tomado la decisión de hacerlo).
b) Bayes ingenuo (como también ACH) es más efectivo cuando se usa para estudiar una situación estable, cuando la evidencia se puede recolectar durante un período de tiempo suficientemente largo sin que la “incógnita” que intentamos resolver cambie apreciablemente. Porque cuando la “incógnita” cambia con relativa rapidez, como suele ser el caso durante las crisis actuales, diferentes observaciones realizadas en momentos distintos pueden ser producto de una “realidad oculta” que se ha modificado, que ya no es la misma. Por eso, si queremos que Bayes ingenuo funcione razonablemente bien con situaciones dinámicas, la recogida de datos debe realizarse en plazos de tiempo relativamente cortos. O debemos descartar los “sucesos” más antiguos, que pueden responder a una “realidad oculta” que ya no es real.
c) Más importante que las dos técnicas que hemos examinado en este post es la “lógica bayesiana” que subyace a ambas. En inteligencia (sobre todo, en inteligencia estratégica) es raro conseguir evidencias directas sobre la realidad que nos interesa. Esa realidad siempre permanece oculta a nuestros ojos y lo que podemos averiguar sobre ella es gracias a sus manifestaciones visibles.
d) Quien quiera ocultar una información valiosa no solo intentará protegerla de intentos directos de acceder a ella, sino que tendrá también en cuenta esas manifestaciones visibles, tan difíciles de ocultar. Y lo hará utilizando desinformación. Este es el principal problema para utilizar Bayes ingenuo (o ACH): distinguir la información correcta de la inexacta y de la desinformacón.
Y es que no resulta nada fácil ser un analista inteligente.
[1] SOMIEDO, J.P. (2018). El análisis bayesiano como piedra angular de la inteligencia de alertas estratégicas. Revista de Estudios en Seguridad Internacional, 4, 1: 161-176. DOI: http://dx.doi.org/10.18847/1.7.10. Para una lista de las interesantes aportaciones de Somiedo al estudio de la metodología del análisis de inteligencia, ver https://dialnet.unirioja.es/servlet/autor?codigo=3971893.
[2] Para una explicación rápida del teorema de Bayes, véase https://es.wikipedia.org/wiki/Teorema_de_Bayes.
[3] Puede verse, por ejemplo, FISK, C.F. (1967). The Sino-Soviet Border Dispute: A Comparison of the Conventional and Bayesian Methods for Intelligence Warning. CIA Center for the Study of Intelligence. https://www.cia.gov/library/center-for-the-study-of-intelligence/kent-csi/vol16no2/html/v16i2a04p_0001.htm (acceso: 08.062020).
[4] Los no familiarizados con las redes bayesianas pueden encontrar una introducción elemental de este concepto en https://es.wikipedia.org/wiki/Red_bayesiana.
[5] Ver STICHA, P., BUEDE, D. & REES, R.L. (2005). APOLLO: An analytical tool for predicting a subject’s decision making. En Proceedings of the 2005 International Conference on Intelligence Analysis. https://cse.sc.edu/~mgv/BNSeminar/ApolloIA05.pdf (acceso: 08.06.2020).
[6] Los que conozcan el histórico concurso de televisión Un, dos, tres, responda otra vez recordarán que una táctica muy eficaz para responder consistía en repetir un “objeto”, alterando alguna de sus características. Por ejemplo, si pedían “muebles que puedan estar en un comedor”, ir diciendo sucesivamente “silla blanca”, “silla negra”, “silla roja”, etc. Esta táctica aplicada a la técnica de “Bayes ingenuo” nos acabaría conduciendo inexorablemente a una hipótesis predeterminada. Claro que sería como hacernos trampas al solitario…
[7] El nombre de la hoja es bayes_excel.xlsx, y puede encontrarse en https://bit.ly/2An58uc.
[8] MCLAUGHLIN, J., & PATÉ-CORNELL, M.E. (2005). A Bayesian approach to Iraq’s nuclear program intelligence analysis: a hypothetical illustration. En 2005 International Conference on Intelligence Analysis. https://analysis.mitre.org/proceedings/Final_Papers_Files/85_Camera_Ready_Paper.pdf (acceso: 27.10.2018). También, MCLAUGHLIN, J. (2005). A Bayesian Updating Model for Intelligence Analysis:A Case Study of Iraq’s Nuclear Weapons Program. Honors Program in International Security Studies Center for International Security and Cooperation Stanford University.
[9] Puede accederse a ella en la siguiente dirección: https://bit.ly/30veoY3.
[10] Puede encontrarse en https://bit.ly/3dUsENL.
Fuente: serviciosdeinteligencia.com, 2020
Algoritmos Naive Bayes: Fundamentos e Implementación
¡Conviértete en un maestro de uno de los algoritmos mas usados en clasificación!
Por Víctor Román.
Victor RomanFollowApr 25, 2019 · 13 min read

Introducción: ¿Qué son los modelos Naive Bayes?
En un sentido amplio, los modelos de Naive Bayes son una clase especial de algoritmos de clasificación de Aprendizaje Automatico, o Machine Learning, tal y como nos referiremos de ahora en adelante. Se basan en una técnica de clasificación estadística llamada “teorema de Bayes”.
Estos modelos son llamados algoritmos “Naive”, o “Inocentes” en español. En ellos se asume que las variables predictoras son independientes entre sí. En otras palabras, que la presencia de una cierta característica en un conjunto de datos no está en absoluto relacionada con la presencia de cualquier otra característica.
Proporcionan una manera fácil de construir modelos con un comportamiento muy bueno debido a su simplicidad.
Lo consiguen proporcionando una forma de calcular la probabilidad ‘posterior’ de que ocurra un cierto evento A, dadas algunas probabilidades de eventos ‘anteriores’.

Ejemplo
Presentaremos los conceptos principales del algoritmo Naive Bayes estudiando un ejemplo.
Consideremos el caso de dos compañeros que trabajan en la misma oficina: Alicia y Bruno. Sabemos que:
- Alicia viene a la oficina 3 días a la semana.
- Bruno viene a la oficina 1 día a la semana.
Esta sería nuestra información “anterior”.
Estamos en la oficina y vemos pasar delante de nosotros a alguien muy rápido, tan rápido que no sabemos si es Alicia o Bruno.
Dada la información que tenemos hasta ahora y asumiendo que solo trabajan 4 días a la semana, las probabilidades de que la persona vista sea Alicia o Bruno, son:
- P(Alicia) = 3/4 = 0.75
- P(Bruno) = 1/4 = 0.25
Cuando vimos a la persona pasar, vimos que él o ella llevaba una chaqueta roja. También sabemos lo siguiente:
- Alicia viste de rojo 2 veces a la semana.
- Bruno viste de rojo 3 veces a la semana.
Así que, para cada semana de trabajo, que tiene cinco días, podemos inferir lo siguiente:
- La probabilidad de que Alicia vista de rojo es → P(Rojo|Alicia) = 2/5 = 0.4
- La probabilidad de que Bruno vista de rojo → P(Rojo|Bruno) = 3/5 = 0.6
Entonces, con esta información, ¿a quién vimos pasar? (en forma de probabilidad)
Esta nueva probabilidad será la información ‘posterior’.

Inicialmente conocíamos las probabilidades P(Alicia) y P(Bruno), y después inferíamos las probabilidades de P(rojo|Alicia) y P(rojo|Bruno).
De forma que las probabilidades reales son:

Formalmente, el gráfico previo sería:

Algoritmo Naive Bayes Supervisado
A continuación se listan los pasos que hay que realizar para poder utilizar el algoritmo Naive Bayes en problemas de clasificación como el mostrado en el apartado anterior.
- Convertir el conjunto de datos en una tabla de frecuencias.
- Crear una tabla de probabilidad calculando las correspondientes a que ocurran los diversos eventos.
- La ecuación Naive Bayes se usa para calcular la probabilidad posterior de cada clase.
- La clase con la probabilidad posterior más alta es el resultado de la predicción.
Puntos fuertes y débiles de Naive Bayes
Los puntos fuertes principales son:
- Un manera fácil y rápida de predecir clases, para problemas de clasificación binarios y multiclase.
- En los casos en que sea apropiada una presunción de independencia, el algoritmo se comporta mejor que otros modelos de clasificación, incluso con menos datos de entrenamiento.
- El desacoplamiento de las distribuciones de características condicionales de clase significan que cada distribución puede ser estimada independientemente como si tuviera una sola dimensión. Esto ayuda con problemas derivados de la dimensionalidad y mejora el rendimiento.
Los puntos débiles principales son:
- Aunque son unos clasificadores bastante buenos, los algoritmos Naive Bayes son conocidos por ser pobres estimadores. Por ello, no se deben tomar muy en serio las probabilidades que se obtienen.
- La presunción de independencia Naive muy probablemente no reflejará cómo son los datos en el mundo real.
- Cuando el conjunto de datos de prueba tiene una característica que no ha sido observada en el conjunto de entrenamiento, el modelo le asignará una probabilidad de cero y será inútil realizar predicciones. Uno de los principales métodos para evitar esto, es la técnica de suavizado, siendo la estimación de Laplace una de las más populares.
Proyecto de Implementación: Detector de Spam
Actualmente, una de las aplicaciones principales de Machine Learning es la detección de spam. Casi todos los servicios de email más importantes proporcionan un detector de spam que clasifica el spam automáticamente y lo envía al buzón de “correo no deseado”.
En este proyecto, desarrollaremos un modelo Naive Bayes que clasifica los mensajes SMS como spam o no spam (‘ham’ en el proyecto). Se basará en datos de entrenamiento que le proporcionaremos.
Haciendo una investigación previa, encontramos que, normalmente, en los mensajes de spam se cumple lo siguiente:
- Contienen palabras como: ‘gratis’, ‘gana’, ‘ganador’, ‘dinero’ y ‘premio’.
- Tienden a contener palabras escritas con todas las letras mayúsculas y tienden al uso de muchos signos de exclamación.
Esto es un problema de clasificación binaria supervisada, ya que los mensajes son o ‘Spam’ o ‘No spam’ y alimentaremos un conjunto de datos etiquetado para entrenar el modelo.
Visión general
Realizaremos los siguientes pasos:
- Entender el conjunto de datos
- Procesar los datos
- Introducción al “Bag of Words” (BoW) y la implementación en la libreria Sci-kit Learn
- División del conjunto de datos (Dataset) en los grupos de entrenamiento y pruebas
- Aplicar “Bag of Words” (BoW) para procesar nuestro conjunto de datos
- Implementación de Naive Bayes con Sci-kit Learn
- Evaluación del modelo
- Conclusión
Entender el Conjunto de Datos
Utilizaremos un conjunto de datos del repositorio UCI Machine Learning.
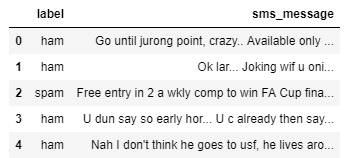
Un primer vistazo a los datos:

Las columnas no se han nombrado, pero como podemos imaginar al leerlas:
- La primera columna determina la clase del mensaje, o ‘spam’ o ‘ham’ (no spam).
- La segunda columna corresponde al contenido del mensaje
Primero importaremos el conjunto de datos y cambiaremos los nombre de las columnas. Haciendo una exploración previa, también vemos que el conjunto de datos está separado. El separador es ‘\t’.
# Importar la libreria Pandas
import pandas as pd# Dataset de https://archive.ics.uci.edu/ml/datasets/SMS+Spam+Collection
df = pd.read_table('smsspamcollection/SMSSpamCollection',
sep='\t',
names=['label','sms_message'])# Visualización de las 5 primeras filas
df.head()
Preprocesamiento de Datos
Ahora, ya que el Sci-kit learn solo maneja valores numéricos como entradas, convertiremos las etiquetas en variables binarias, 0 representará ‘ham’ y 1 representará ‘spam’.
Para representar la conversión:
# Conversion
df['label'] = df.label.map({'ham':0, 'spam':1})# Visualizar las dimensiones de los datos
df.shape()

Introducción a la Implementación “Bag of Words” (BoW) y Sci-kit Learn
Nuestro conjunto de datos es una gran colección de datos en forma de texto (5572 filas). Como nuestro modelos solo aceptará datos numéricos como entrada, deberíamos procesar mensajes de texto. Aquí es donde “Bag of Words“ entra en juego.
“Bag of Words” es un término usado para especificar los problemas que tiene una colección de datos de texto que necesita ser procesada. La idea es tomar un fragmento de texto y contar la frecuencia de las palabras en el mismo.
BoW trata cada palabra independientemente y el orden es irrelevante.
Podemos convertir un conjunto de documentos en una matriz, siendo cada documento una fila y cada palabra (token) una columna, y los valores correspondientes (fila, columna) son la frecuencia de ocurrencia de cada palabra (token) en el documento.
Como ejemplo, si tenemos los siguientes cuatro documentos:
['Hello, how are you!', 'Win money, win from home.', 'Call me now', 'Hello, Call you tomorrow?']
Convertiremos el texto a una matriz de frecuencia de distribución como la siguiente:

Los documentos se numeran en filas, y cada palabra es un nombre de columna, siendo el valor correspondiente la frecuencia de la palabra en el documento.
Usaremos el método contador de vectorización de Sci-kit Learn, que funciona de la siguiente manera:
- Fragmenta y valora la cadena (separa la cadena en palabras individuales) y asigna un ID entero a cada fragmento (palabra).
- Cuenta la ocurrencia de cada uno de los fragmentos (palabras) valorados.
- Automáticamente convierte todas las palabras valoradas en minúsculas para no tratar de forma diferente palabras como “el” y “El”.
- También ignora los signos de puntuación para no tratar de forma distinta palabras seguidas de un signo de puntuación de aquellas que no lo poseen (por ejemplo “¡hola!” y “hola”).
- El tercer parámetro a tener en cuenta es el parámetro
stop_words. Este parámetro se refiere a las palabra más comúnmente usadas en el lenguaje. Incluye palabras como “el”, “uno”, “y”, “soy”, etc. Estableciendo el valor de este parámetro por ejemplo enenglish, “CountVectorizer” automáticamente ignorará todas las palabras (de nuestro texto de entrada) que se encuentran en la lista de “stop words” de idioma inglés..
La implementación en Sci-kit Learn sería la siguiente:
# Definir los documentos
documents = ['Hello, how are you!',
'Win money, win from home.',
'Call me now.',
'Hello, Call hello you tomorrow?']# Importar el contador de vectorizacion e inicializarlo
from sklearn.feature_extraction.text import CountVectorizer
count_vector = CountVectorizer()# Visualizar del objeto'count_vector' que es una instancia de 'CountVectorizer()'
print(count_vector)

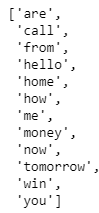
Para ajustar el conjunto de datos del documento al objeto “CountVectorizer” creado, usaremos el método “fit()”, y conseguiremos la lista de palabras que han sido clasificadas como características usando el método “get_feature_names()”. Este método devuelve nuestros nombres de características para este conjunto de datos, que es el conjunto de palabras que componen nuestro vocabulario para “documentos”.
count_vector.fit(documents)
names = count_vector.get_feature_names()
names
A continuación, queremos crear una matriz cuyas filas serán una de cada cuatro documentos, y las columnas serán cada palabra. El valor correspondiente (fila, columna) será la frecuencia de ocurrencia de esa palabra (en la columna) en un documento particular (en la fila).
Podemos hacer esto usando el método “transform()” y pasando como argumento en el conjunto de datos del documento. El método “transform()” devuelve una matriz de enteros, que se puede convertir en tabla de datos usando “toarray()”.
doc_array = count_vector.transform(documents).toarray()
doc_array

Para hacerlo fácil de entender, nuestro paso siguiente es convertir esta tabla en una estructura de datos y nombrar las columnas adecuadamente.
frequency_matrix = pd.DataFrame(data=doc_array, columns=names)
frequency_matrix

Con esto, hemos implementado con éxito un problema de “BoW” o Bag of Words para un conjunto de datos de documentos que hemos creado.
Un problema potencial que puede surgir al usar este método es el hecho de que si nuestro conjunto de datos de texto es extremadamente grande, habrá ciertos valores que son más comunes que otros simplemente debido a la estructura del propio idioma. Así, por ejemplo, palabras como ‘es’, ‘el’, ‘a’, pronombres, construcciones gramaticales, etc. podrían sesgar nuestra matriz y afectar nuestro análisis.
Para mitigar esto, usaremos el parámetro stop_words de la clase CountVectorizer y estableceremos su valor en inglés.
Dividiendo el Conjunto de Datos en Conjuntos de Entrenamiento y Pruebas
Buscamos dividir nuestros datos para que tengan la siguiente forma:
X_trainson nuestros datos de entrenamiento para la columna ‘sms_message’y_trainson nuestros datos de entrenamiento para la columna ‘label’X_testson nuestros datos de prueba para la columna ‘sms_message’y_testson nuestros datos de prueba para la columna ‘label’. Muestra el número de filas que tenemos en nuestros datos de entrenamiento y pruebas
# Dividir los datos en conjunto de entrenamiento y de test
from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(df['sms_message'], df['label'], random_state=1)print('Number of rows in the total set: {}'.format(df.shape[0]))print('Number of rows in the training set: {}'.format(X_train.shape[0]))print('Number of rows in the test set: {}'.format(X_test.shape[0]))

Aplicar BoW para Procesar Nuestros Datos de Pruebas
Ahora que hemos dividido los datos, el próximo objetivo es convertir nuestros datos al formato de la matriz buscada. Para realizar esto, utilizaremos CountVectorizer() como hicimos antes. tenemos que considerar dos casos:
- Primero, tenemos que ajustar nuestros datos de entrenamiento (
X_train) enCountVectorizer()y devolver la matriz. - Sgundo, tenemos que transformar nustros datos de pruebas (
X_test) para devolver la matriz.
Hay que tener en cuenta que X_train son los datos de entrenamiento de nuestro modelo para la columna ‘sms_message’ en nuestro conjunto de datos.
X_test son nuestros datos de prueba para la columna ‘sms_message’, y son los datos que utilizaremos (después de transformarlos en una matriz) para realizar predicciones. Compararemos luego esas predicciones con y_test en un paso posterior.
El código para este segmento está dividido en 2 partes. Primero aprendemos un diccionario de vocabulario para los datos de entrenamiento y luego transformamos los datos en una matriz de documentos; segundo, para los datos de prueba, solo transformamos los datos en una matriz de documentos.
# Instantiate the CountVectorizer method
count_vector = CountVectorizer()# Fit the training data and then return the matrix
training_data = count_vector.fit_transform(X_train)# Transform testing data and return the matrix. Note we are not fitting the testing data into the CountVectorizer()
testing_data = count_vector.transform(X_test)
Implementación Naive Bayes con Sci-Kit Learn
Usaremos la implementación Naive Bayes “multinomial”. Este clasificador particular es adecuado para la clasificación de características discretas (como en nuestro caso, contador de palabras para la clasificación de texto), y toma como entrada el contador completo de palabras.
Por otro lado el Naive Bayes gausiano es más adecuado para datos continuos ya que asume que los datos de entrada tienen una distribución de curva de Gauss (normal).
Importaremos el clasificador “MultinomialNB” y ajustaremos los datos de entrenamiento en el clasificador usando fit().
from sklearn.naive_bayes import MultinomialNB
naive_bayes = MultinomialNB()
naive_bayes.fit(training_data, y_train)

Ahora que nuestro algoritmo ha sido entrenado usando el conjunto de datos de entrenamiento, podemos hacer algunas predicciones en los datos de prueba almacenados en ‘testing_data’ usando predict().
predictions = naive_bayes.predict(testing_data)
Una vez realizadas las predicciones el conjunto de pruebas, necesitamos comprobar la exactitud de las mismas.
Evaluación del modelo
Hay varios mecanismos para hacerlo, primero hagamos una breve recapitulación de los criterios y de la matriz de confusión.
- La matriz de confusión es donde se recogen el conjunto de posibilidades entre la clase correcta de un evento, y su predicción.
- Exactitud: mide cómo de a menudo el clasificador realiza la predicción correcta. Es el ratio de número de predicciones correctas contra el número total de predicciones (el número de puntos de datos de prueba).
- Precisión: nos dice la proporción de mensajes que clasificamos como spam. Es el ratio entre positivos “verdaderos” (palabras clasificadas como spam que son realmente spam) y todos los positivos (palabras clasificadas como spam, lo sean realmente o no)
- Recall (sensibilidad): Nos dice la proporción de mensajes que realmente eran spam y que fueron clasificados por nosotros como spam. Es el ratio de positivos “verdaderos” (palabras clasificadas como spam, que son realmente spam) y todas las palabras que fueron realmente spam.
Para los problemas de clasificación que están sesgados en sus distribuciones de clasificación como en nuestro caso. Por ejemplo si tuviéramos 100 mensajes de texto y solo 2 fueron spam y los restantes 98 no lo fueron, la exactitud por si misma no es una buena métrica. Podríamos clasificar 90 mensajes como no spam (incluyendo los 2 que eran spam y los clasificamos como “no spam”, y por tanto falsos negativos) y 10 como spam (los 10 falsos positivos) y todavía conseguir una puntuación de exactitud razonablemente buena.
Para casos como este, la precisión y el recuerdo son bastante adecuados. Estas dos métricas pueden ser combinadas para conseguir la puntuación F1, que es el “peso” medio de las puntuaciones de precisión y recuerdo. Esta puntuación puede ir en el rango de 0 a 1, siendo 1 la mejor puntuación posible F1.
Usaremos las cuatro métricas para estar seguros de que nuestro modelo se comporta correctamente. Para todas estas métricas cuyo rango es de 0 a 1, tener una puntuación lo más cercana posible a 1 es un buen indicador de cómo de bien se está comportando el modelo.
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_scoreprint('Accuracy score: ', format(accuracy_score(y_test, predictions)))print('Precision score: ', format(precision_score(y_test, predictions)))print('Recall score: ', format(recall_score(y_test, predictions)))print('F1 score: ', format(f1_score(y_test, predictions)))

Conclusión
- Una de las mayores ventajas que Naive Bayes tiene sobre otros algoritmos de clasificación es la capacidad de manejo de un número extremadamente grande de características. En nuestro caso, cada palabra es tratada como una característica y hay miles de palabras diferentes.
- También, se comporta bien incluso ante la presencia de características irrelevantes y no es relativamente afectado por ellos.
- La otra ventaja principal es su relativa simplicidad. Naive Bayes funciona bien desde el principio y ajustar sus parámetros es raramente necesario.
- Raramente sobreajusta los datos.
- Otra ventaja importante es que su modelo de entrenamiento y procesos de predicción son muy rápidos teniendo en cuenta la cantidad de datos que puede manejar.
Fuente: medium.com, 2019

Vincúlese a nuestras Redes Sociales:
LinkedIn YouTube Facebook Twitter
.
.



