Ética pública: funcionarios y candidatos simultáneos

Por Fishel Szlajen.

En los sistemas republicanos y las democracias representativas, la legitimidad de los funcionarios no sólo se sustenta en el mandato electoral o designación política dentro de los términos legales, sino también en el cumplimiento de estándares de ética pública que garanticen la equidad en la competencia política reglando su conducta conforme a los valores democráticos.

.

Así, la simultaneidad entre la postulación a un cargo público y el ejercicio de otro, cuando este facilita medios estatales de alto valor para campañas políticas, despierta sospechas de uso indebido del poder y de los recursos del Estado con fines proselitistas, comprometiendo la integridad del proceso electoral y la confianza ciudadana por abuso de poder o posición de privilegio frente a otros candidatos.

La función pública se rige por principios de legalidad, transparencia, equidad e integridad en el uso de los recursos públicos. Según el Código Iberoamericano de Buen Gobierno, la actuación gubernamental debe alejarse del reprobable abuso de los recursos públicos para fines de interés partidista o particular, debiendo el funcionario abstenerse de conductas que comprometan la neutralidad en el ejercicio de los servicios públicos que tuviera encomendados. A su vez, la Convención de Naciones Unidas contra la Corrupción recomienda establecer normas que aseguren la separación entre funciones públicas y actividades proselitistas manifestando que no toda conducta ética debe esperar a ser tipificada penalmente para ser corregida institucionalmente.

Desde la sociología, Max Weber advierte sobre el uso del Estado con fines partidarios, y más aún naturalizando el uso de recursos públicos como plataformas implícitas de campaña.

Desde la filosofía del derecho, Thomas Nagel indica que el conflicto de interés en un funcionario surge ante la posible interferencia con el cumplimiento imparcial de sus deberes. Así, ejercer un cargo mientras se realiza campaña para ocupar otro, puede derivar en decisiones públicas orientadas a obtener rédito electoral. Y aun cuando no quiebre la ley, socava la confianza pública y degrada el proceso democrático.

Desde la filosofía política, Michael Walzer plantea que poseyendo cada esfera de la justicia distributiva sus propias reglas, es injusto trasladar privilegios de una esfera a otra, por ejemplo, del cargo público usando el poder político al rédito electoral, denominándolo dominación cruzada.

Y desde la ciencia política, Robert Dahl demuestra que estas prácticas minan la equidad electoral porque la competencia democrática exige igualdad de condiciones para participar en la contienda política. Un funcionario, y más quien desempeña labores cuya visibilidad es inherente a su cargo, posee evidentes ventajas en campaña respecto de los recursos de candidatos ajenos al gobierno, viciando el principio de fair play democrático.

Todo ello alerta sobre el daño al sistema democrático y republicano desalentando la participación política y erosionando la credibilidad de las instituciones, porque como advierte Seymour Lipset, la legitimidad democrática depende de que las reglas sean vistas como justas.

Ahora bien, desde una ética de la responsabilidad pública, la opción de solicitar licencia temporal parece insuficiente si no va acompañada de un control estricto sobre el uso de recursos públicos. Por ello, algunos organismos recomiendan la renuncia como mecanismo de integridad institucional, así indicado por la OCDE en su Guidelines for Managing Conflict of Interest in the Public Service.

Sin embargo, hay posiciones que consideran suficiente la licencia, en la medida en que esta impida el acceso a recursos estatales, así sugerido por Jeremy Waldron cuando distingue entre conflicto de interés y uso ilegítimo del poder donde la ambición política debe separarse completamente del aparato estatal.

En Brasil, la Ley Complementaria 64/1990 establece la llamada “desincompatibilización” obligatoria por la cual los funcionarios deben cesar en sus funciones tres o seis meses antes presentarse a elecciones para evitar el uso de la maquinaria estatal como ventaja. En Chile, la Ley Orgánica Constitucional de Municipalidades obliga a los alcaldes a renunciar con antelación si desean postularse a otros cargos. En México, la Ley General de Instituciones y Procedimientos Electorales establece requisitos de separación para candidatos provenientes de la función pública. Estados Unidos no posee una norma federal que obligue a renunciar, pero algunos estados y jurisdicciones locales tienen “resign-to-run laws” requieriendo que los funcionarios renuncien antes de postularse para otro cargo. En Alemania, Martin Schulz renunció como presidente del Parlamento Europeo antes de postularse a canciller por el SPD en 2017. Dicha renuncia fue interpretada como un acto de respeto institucional y de ética pública.

Argentina carece de una norma general obligatoria de licencia o renuncia, y sumada a una clase política tendiente al abuso de poder, ha manifestado recientemente el caso paradigmático contrario a todas las mencionadas especificaciones y recomendaciones. Fue la candidatura presidencial del entonces Ministro de Economía, Sergio Massa, la cual generó severas críticas por no haber renunciado y haber mantenido una intensa agenda pública coincidente con su campaña utilizando todos los recursos estatales más su posición de privilegio para construir su imagen electoral, lo que resultó en serios perjuicios económicos inflacionarios para todos los Argentinos.

.

La jurisprudencia de la CSJN en Gutiérrez, Esteban c/Estado Nacional, ha afirmado que el deber de decoro y legalidad administrativa alcanza no sólo los actos públicos, sino también las condiciones éticas que deben rodear al desempeño del cargo. La misma CSJN, en Camaño c/Estado Nacional, sostuvo que la ética pública no se reduce al cumplimiento de la ley, sino que implica preservar la confianza pública en la neutralidad y transparencia del accionar estatal, más aún en los procesos electorales.

Ahora bien, estas consideraciones no aplican para las reelecciones porque el funcionario que busca ser reelegido no está utilizando su cargo como un plataforma hacia una nueva esfera de poder, sino que reitera su aspiración al mismo mandato conferido por el electorado, en continuidad con la legitimidad previa. Giovanni Sartori lo justifica porque la reelección no es una conquista nueva del poder, sino la renovación del contrato político previo. Por lo tanto, no necesariamente viola los principios de equidad en tanto se respeten las reglas de la competencia y sin utilizar recursos públicos con fines partidarios. Más, el uso del cargo en campaña de reelección debería ser una rendición de cuentas presentando el candidato su gestión ante el electorado. En adición a ello, autores como Bernard Manin observaron que los cargos ejecutivos implican una exposición mediática permanente, haciendo prácticamente imposible separar las funciones de campaña de aquellas institucionales durante períodos electorales. Luego, de exigir licencia o renuncia a todo funcionario a reelegirse paralizaría la administración en cada elección. Por ello, la solución práctica es permitir la reelección sin licencia, pero reglar la publicidad oficial y el uso de recursos públicos, actualmente normalizado en leyes tales como la 26.571 y 26.215. No obstante, dicha falta de licencia en procesos electorales reelectivos se debería compensar con límites a la reelección evitando que la ventaja del cargo derive en una perpetuación ilegítima en el poder. Aquí el abuso no está en la candidatura, sino en la captura institucional del poder sin alternancia.

Conclusión, resulta razonable exigir a todo funcionario que aspira a otro cargo una separación formal, efectiva y verificable de sus actuales funciones, por licencia o renuncia acorde al nivel de poder e influencia institucional. Porque la tan mentada batalla cultural, demanda estándares éticos en la política preservando la equidad, la transparencia e integridad, exigiendo instituciones y procedimientos justos para todos.

Fuente: infobae.com, 10/04/25

---

Más información:

El Teorema de Imposibilidad de Arrow: La complejidad de la Democracia Representativa

.

.

El Teorema de Imposibilidad de Arrow: La complejidad de la Democracia Representativa

Por Gustavo Ibáñez Padilla.

En el corazón de cualquier sistema democrático se encuentra el desafío de representar fielmente las preferencias de un grupo diverso de individuos. Sin embargo, Kenneth Arrow, distinguido economista y matemático, enunció en 1951 un teorema que arrojó una sombra sobre esta noble empresa. El Teorema de Imposibilidad de Arrow, también conocido como Paradoja de Arrow, revela las limitaciones fundamentales que enfrentan los sistemas de votación al intentar reflejar de manera justa las voluntades de los ciudadanos.

El Teorema establece que cuando los votantes tienen tres o más alternativas, no es posible diseñar un sistema de votación que permita reflejar las preferencias de los individuos en una preferencia global de la comunidad de modo que al mismo tiempo se cumplan ciertos criterios racionales. A continuación, analizaremos en detalle este teorema, así como sus tres condiciones esenciales: la ausencia de un dictador, la eficiencia de Pareto y la independencia de alternativas irrelevantes.

1. Ausencia de un «dictador»

Uno de los pilares del Teorema de Imposibilidad de Arrow es la ausencia de un ‘dictador’. En este contexto, el término no se refiere a un líder autoritario, sino a un individuo que posea el poder de imponer sus preferencias sobre el grupo, sin importar las de los demás. Arrow demostró que en un sistema de votación donde existe un dictador, las preferencias de los demás miembros del grupo quedan subyugadas, lo cual contradice el principio democrático de igualdad de voz y voto.

2. Eficiencia de Pareto

La eficiencia de Pareto es una condición que establece que si todos los miembros de un grupo prefieren una opción A sobre una opción B, entonces la elección del grupo también debería reflejar esta preferencia. Es decir, si una opción es considerada por todos como preferible a otra, no debería haber obstáculos que impidan su elección. El Teorema de Imposibilidad de Arrow muestra que esta condición es extremadamente difícil de satisfacer en sistemas de votación con tres o más opciones.

3. Independencia de Alternativas irrelevantes

Esta condición postula que el resultado de una votación no debe cambiar si se eliminan opciones que no tienen posibilidad de ser elegidas. En otras palabras, el cambio en las preferencias entre las opciones restantes no debería afectar el resultado. Arrow demostró que esta condición es particularmente complicada de mantener en sistemas de votación con múltiples opciones.

.

Ejemplos y Aplicaciones

Para ilustrar la influencia del Teorema de Imposibilidad de Arrow en situaciones de votación electoral, podemos analizar las elecciones presidenciales del año 2000 en Estados Unidos. El conflicto entre George W. Bush y Al Gore, junto con la presencia de un tercer candidato, Ralph Nader, demostró los desafíos que enfrenta un sistema de votación al intentar reflejar las preferencias de los ciudadanos de manera precisa.

En el sistema estadounidense de las elecciones presidenciales, el voto en el colegio electoral determina el ganador, y Bush ganó esta cuenta, aunque Gore recibió el mayor número de votos (la llamada votación popular).

• G. W. Bush: votos 50.456.002; electores 271.

• A. Gore: votos 50.999.897; electores 266.

• R. Nader: votos 2.882.955; electores 0.

En el contexto histórico, este teorema ha influido en la evolución de sistemas de votación alrededor del mundo. La introducción de métodos como la votación por rangos y la representación proporcional son respuestas directas a las limitaciones identificadas por Arrow. Estos sistemas buscan abordar los problemas de dictadores potenciales, eficiencia de Pareto e independencia de alternativas irrelevantes de manera más efectiva que los métodos de votación tradicionales.

.

Soluciones Innovadoras

Diversos sistemas de elección han sido propuestos para suavizar las restricciones impuestas por el Teorema de Imposibilidad de Arrow. Uno de los más destacados es la votación por rangos, utilizado en elecciones de múltiples candidatos. En este sistema, los votantes clasifican a los candidatos según sus preferencias, permitiendo una elección más precisa y reflejando mejor la voluntad del electorado.

Otro enfoque es la representación proporcional (por ejemplo el sistema D’Hondt), implementada en varios países para asegurar que los partidos políticos obtengan escaños en proporción a su apoyo popular. Este sistema busca evitar la distorsión de la representación que puede ocurrir en sistemas de mayoría simple.

.

Para concluir

El Teorema de Imposibilidad de Arrow ha marcado un hito crucial en el campo de la teoría de la elección y la democracia representativa. Nos recuerda que no existe un sistema de votación perfecto y que siempre habrá desafíos inherentes a la representación fiel de las preferencias de un grupo diverso de individuos. Sin embargo, a pesar de sus limitaciones, este teorema ha estimulado la búsqueda de métodos de votación más justos y equitativos.

En última instancia, el Teorema de Imposibilidad de Arrow nos insta a no conformarnos con soluciones simplistas, sino a seguir buscando maneras innovadoras de fortalecer nuestras democracias. Su importancia radica en su capacidad para estimular el pensamiento crítico y la innovación en el diseño de sistemas electorales, lo que en última instancia contribuye a la construcción de sociedades más justas y equitativas.

Fuente: Ediciones EP, 04/10/23.

---

.

.

Gerrymandering: Una burla a la Democracia

Gerrymandering: cuando los políticos eligen a sus votantes

INVESTIGACIÓN UPV/EHU

Por Annick Laruelle.

Para muchos estados, la representación en el congreso tiene que ser geográfica e igualitaria. El objetivo geográfico se obtiene dividiendo el país en circunscripciones electorales. Tradicionalmente hay dos formas de conseguir el objetivo igualitario. En los sistemas proporcionales cada circunscripción tiene un número de representantes que depende de su población. En los sistemas mayoritarios las circunscripciones tienen poblaciones parecidas y cada una de ellas tiene un único representante.

Cada diez años, se realiza el censo de la población en EEUU. El último fue en 2020. Éste va a determinar el número de escaños que tendrá cada estado en la Cámara de los Representantes hasta 2030. Según las primeras estimaciones unos 17 estados podrían ver su número de escaños afectado, lo que modificará el reparto de poder entre los estados.

Los datos del censo sirven también para garantizar que todas las circunscripciones electorales de un estado tengan poblaciones parecidas. En 2021 las fronteras de las circunscripciones se modificarán para satisfacer este objetivo. El diseño no es neutral, puede determinar el resultado electoral. Sin embargo, el dibujo de las fronteras está generalmente en manos del poder legislativo.

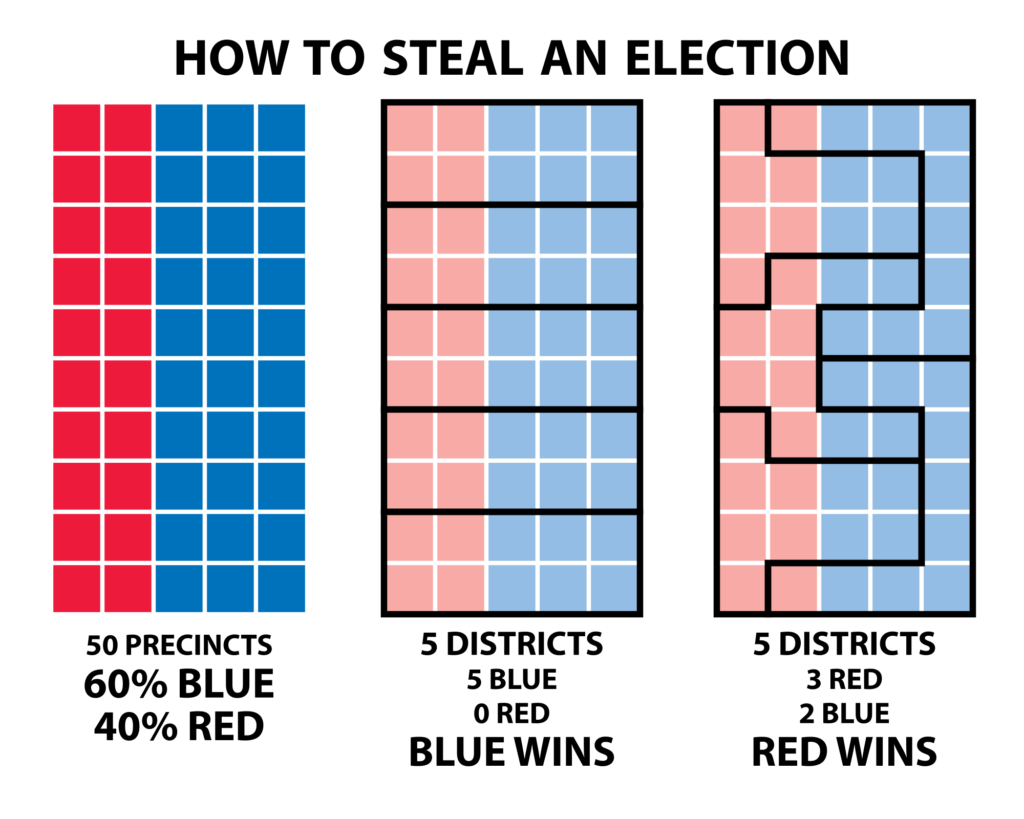
El gerrymandering dibuja las fronteras para favorecer a un grupo de la población o a un partido. El origen del nombre se remonta a 1812 cuando una circunscripción que diseñó el gobernador E. Gerry se caricaturizó como una salamandra (“salamander”).

Los dos lemas del gerrymandering son “dispersión y concentración” (“CRACK and PACK”). Una técnica consiste en dispersar los votos de la oposición para dejarla en minoría en el mayor número de circunscripciones posible. Otra técnica consiste en concentrar los votos de la oposición en un pequeño número de circunscripciones donde la oposición gana con una amplia mayoría. Si las técnicas son muy antiguas, los métodos informáticos son cada vez más sofisticados y la información sobre los electores más extensa.

En 2010 un comité republicano creó el proyecto REDMAP para ayudar a redibujar las circunscripciones después del censo de 2010. Thomas Hofeller, uno los estrategas del proyecto, afirmó en una conferencia que este proceso era una elección a la inversa, en el sentido que permitía a los políticos elegir a sus votantes.

La efectividad del proyecto se puede ilustrar en el estado de Carolina del Norte.

Las 13 circunscripciones dibujadas después del censo de 2010 son muy poco compactas, en particular las con números 1, 4 y 12. En estas tres circunscripciones los demócratas ganaron las elecciones de 2012 y 2014 con porcentajes de votos superior al 70%. Los republicanos ganaron las elecciones en todos las otras circunscripciones (salvo una en 2012) pero con pequeños márgenes.

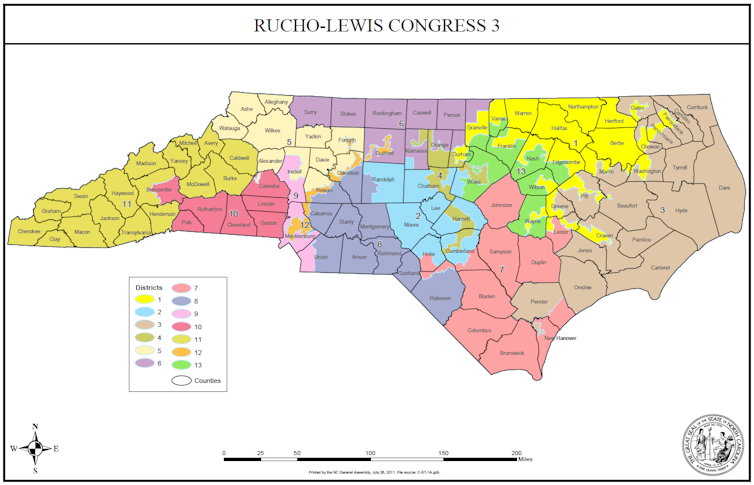
Al nivel global del estado, el partido demócrata consiguió menos de 31% de los escaños (4 de 13) en 2012, aunque recibió casi 51% de los votos. En 2014, obtuvo 44% de los votos, que se tradujeron en 23% de los escaños (3 de 13). En 2016, el tribunal supremo federal declaró el mapa anticonstitucional por gerrymandering de tipo racial. El poder legislativo tuvo que modificarlo.

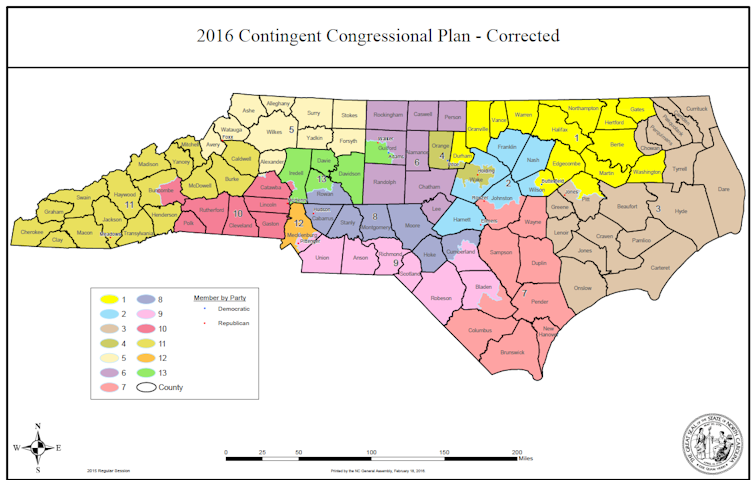
En 2016 y 2018 el partido demócrata obtuvo de nuevo 23% de los escaños a pesar de haber obtenido en ambas elecciones más de 46% de los votos. En 2019 un tribunal estatal reconoció el carácter partidista del mapa electoral modificado. Una vez más el poder legislativo tuvo que redibujar las 13 circunscripciones.

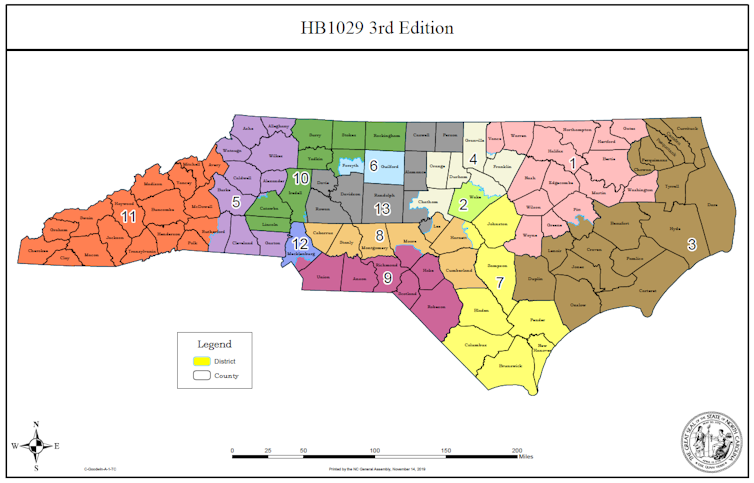
En 2020 la diferencia entre porcentajes de votos y porcentaje de escaños se redujo: los demócratas obtuvieron casi 50% de los votos y 38% de los escaños (5 de 13). El censo realizado en 2020 modificará de nuevo el mapa, en principio con una circunscripción adicional.

Los republicanos no son los únicos que practican el gerrymandering. En 2019 se intentó conseguir la inconstitucionalidad del mapa electoral de Maryland (dibujado por los demócratas). Hasta la fecha los tribunales federales se han negado a condenar el gerrymandering de tipo partidista.

Demostrar la existencia de gerrymandering no es siempre una tarea fácil. No es suficiente constatar que el porcentaje de votos no coincide con el porcentaje de escaños. A veces es la geografía la que genera diferencias entre votos y escaños.

En un artículo reciente investigadores de la universidad de Duke analizaron los mapas electorales de Carolina del Norte. Dibujaron de manera aleatoria más de 66 000 mapas alternativos. Calcularon las distribuciones de escaños que se habrían obtenido con esos mapas. Las distribuciones de escaños obtenidas en las elecciones de 2012 y 2014 ocurren con una frecuencia inferior a 1% con los mapas alternativos, es decir son muy poco probables.

Además mostraron que pequeños cambios en las fronteras de las circunscripciones demócratas habrían modificado de manera sustancial los resultados. Concluyeron la existencia de gerrymandering. Sin embargo, admitieron que la geografía del estado es más favorable a los republicanos que a los demócratas.

Los objetivos de representación geográfica y representación igualitaria son difícilmente compatibles. Quizás es el momento de replantearse la importancia de la representación geográfica en comparación con el objetivo de tratamiento igual para todos los votantes.

Sobre la autora: Annick Laruelle es profesora IKERBASQUE en el Departamento de Análisis Económico de la Universidad del País Vasco / Euskal Herriko Unibertsitatea

Este artículo fue publicado originalmente en The Conversation. Artículo original.

Fuente: culturacientifica.com, 2021

---

.

.

Helmut Norpoth predice que Trump ganará las elecciones

Helmut Norpoth predice de nuevo que Trump ganará las elecciones

Según sus cálculos la victoria de Trump está asegurada de nuevo, con un 90 por ciento de posibilidades, a pesar de lo que marcan las encuestas.

Por Redacción Miami Diario

Helmut Norpoth es profesor del Departamento de Ciencias Políticas de la universidad de Stony Brook. Su figura es extraordinariamente reconocida después de que en el año 2016 predijese acertadamente el resultado de las elecciones presidenciales de Estados Unidos.

El modelo de análisis de Helmut Norpoth, The Primary Model, o el Modelo Primario, se le da al presidente Donald Trump “un 91% de posibilidades de ganar las elecciones presidenciales de 2020″. Por su parte, “el demócrata Joe Biden tiene solo un 9% de posibilidades. Trump obtendría 362 votos electorales, Biden 176”.

Como añade esta página del Modelo Primario, “en 2016, cuando las encuestas, los expertos y los pronosticadores predecían una cierta victoria para Hillary Clinton, el MODELO PRIMARIO estaba prácticamente solo en predecir la victoria de Donald Trump. Lo hizo ya el 7 de marzo de ese año, poniendo sus posibilidades de ganar en 87%”.

“Para que conste”, se explica en la página, este modelo ha acertado con el “ganador de 25 de las 27 elecciones desde 1912, cuando se introdujeron las primarias presidenciales. Los fallos son 1960, una de las elecciones presidenciales más reñidas, y 2000, cuando el último recuento en Florida le dio la victoria a Bush”.

Norpoth añade otro factor a la reelección

Según el politólogo algo particularmente extraño que favorecería a Donald Trump este año, además del resultado de las elecciones primarias republicanas, es el carácter cíclico de la historia electoral de los Estados Unidos. Según el análisis previo al establecimiento de este método, tras un mandato en la Casa Blanca, el partido en el poder es el favorito para ganar la reelección.

No obstante, si se aplica este modelo estadístico y sus principales varas de medir (los resultados en las primarias y la tendencia a la reelección) a todas las elecciones estadounidenses desde 1912, no siempre acierta. De 27 comicios, hay dos en los que fallaría: los de 1960, «una de las elecciones presidenciales más reñidas», y los anteriormente nombrados de 2000, «cuando el último recuento en Florida le dio la victoria a Bush; aun así, Al Gore terminó ganando el voto popular». No ocurrió lo mismo, sin embargo, con las últimas elecciones: el experto en ciencias políticas contradijo a todas las encuestas que daban por sentada la derrota de Trump y apostó por su victoria sobre Hillary Clinton (le dio 87% de probabilidad de éxito). Su estudio fue publicado el 7 de marzo de 2016; el 8 de noviembre de ese mismo año los resultados electorales le dieron la razón.

Poco margen de error

Por su parte, tal y como publicó el corresponsal de ABC en Washington, David Alandete, «las encuestas electorales en Estados Unidos reflejan una distancia por parte de Joe Biden de al menos seis puntos sobre Donald Trump. Lo cierto es que algunos de los sondeos han llegado a reflejar una diferencia de hasta 14 puntos, aunque han sido escasos. Esta semana, la media de sondeos de RealClearPolitics apunta a una distancia del demócrata de casi nueve puntos».

En este sentido, Norpoth afirma que su método es invariable y no tiene en cuenta el momento histórico-social, la popularidad de los candidatos en el momento: «Mi predicción es lo que llamo «final incondiciona». No cambia. Es un modelo matemático basado en cosas que han sucedido. La elección presidencial de 2016 ha sucedido, los resultados de las primarias ya están disponibles. Puedo agregar los resultados de más primarias, pero incluso esos números han sucedido y tampoco pueden cambiar».

Fuente original: Primer Informe

Fuente: miamidiario.com, 01/11/20

.

.