Resolución de un crimen con Teoría de Grafos
septiembre 13, 2022 · Imprimir este artículo
El reto matemático: El crimen de la mujer muerta en su casa de Pirineos, resuelto con grafos
Por Víctor M. Manero.
Hace dos semanas en ‘¿Pueden las matemáticas resolver un crimen?’ de esta sección se presentó un crimen ficticio retando al lector a resolverlo usando matemáticas, en particular, grafos.
Una breve introducción sobre grafos se puede encontrar en dicho artículo, así como el concepto de grafo de intervalos que recordamos aquí.
Grafo de intervalos
Si representamos varios intervalos en una recta real, por ejemplo, podemos pensar en los periodos de tiempo que unas ciertas personas han pasado en una isla ver figura 1, el grafo de dichos intervalos es aquel que se obtiene dibujando un vértice por cada intervalo o persona y dos vértices se unirán con una arista si las personas que representan han coincidido en la isla o lo que es lo mismo si los correspondientes intervalos se intersecan, ver figura 1.
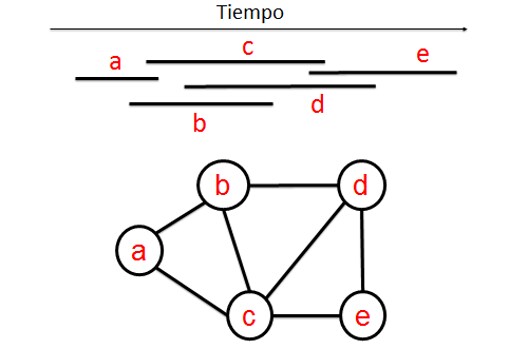
Los grafos de intervalos tienen propiedades interesantes pero la que nos interesa a nosotros es la siguiente:
Un grafo de intervalos siempre está triangulado.
Un grafo se dice que está triangulado si para todo camino cerrado (conjunto de aristas que comienza y acaba en un mismo vértice) formado por al menos al menos cuatro aristas, existe una que une vértices no consecutivos, ver figura 2. Equivalentemente esto se puede describir como que dado cualquier cuadrilátero contenido en el grafo éste está dividido en triángulos.
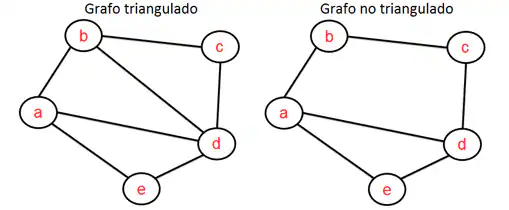
Una justificación informal de esta propiedad es fácil de presentar. Si suponemos que existe un grafo de intervalos con un camino cerrado de longitud cuatro y que no está triangulado, al tratar de construir los correspondientes intervalos que dan lugar a dicho grafo vemos que un tal grafo no puede existir, ver figura 3.
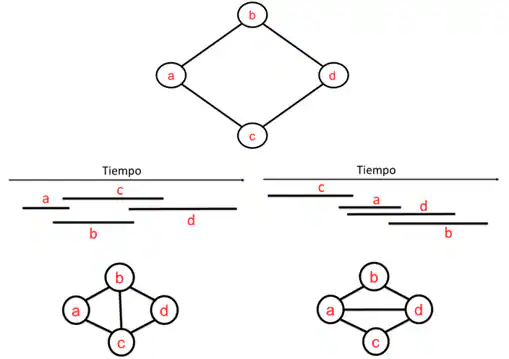
Por lo tanto, si dada una situación al trazar su correspondiente grafo de intervalos resulta que éste no está triangulado esto nos viene a decir que dicho grafo es erróneo o lo que es equivalente los intervalos asociados al mismo están equivocados.
El crimen en cuestión
Acababa de llegar la primavera y la veterana inspectora Alicia Pelegrina de la Policía Nacional se encontraba ante un paisaje plagado de nieve. A su lado, su joven ayudante, el agente Jorge Martín.
A pesar de sus años de experiencia, la inspectora Pelegrina jamás había visto un caso parecido. Una mujer, Araceli, había sido hallada muerta en la casa que habitaba en un abandonado pueblo del Pirineo aragonés del que era la única habitante. Las investigaciones permiten concluir a los agentes Pelegrina y Martín que el crimen se ha producido debido a un escape de gas venenoso accionado con un temporizador. El dispositivo, que había sido minuciosamente instalado, se encontraba escondido en las inmediaciones de la casa y a través de un tubo dirigía el gas letal hasta la misma.
Las primeras pesquisas permiten a los agentes deducir que el crimen ha sido llevado a cabo por una única persona, pero ¿quién?
A lo largo del invierno varias personas habían visitado a la fallecida, concretamente 8. Estas son consideradas desde un primer momento sospechosas. Debido a la intensa nieve todos los visitantes habían accedido al pueblo desde el único acceso posible, la estación de tren de Canfranc. El guardia de seguridad de la estación recuerda haber visto a los 8 sospechosos exactamente en dos ocasiones, una cuando venían y otra cuando se iban, lo que confirma que cada sospechoso visitó a la víctima una única vez. Sin embargo, el guardia no recuerda las fechas exactas de paso de cada uno de ellos.
La lista de los sospechosos es la siguiente:
Laura Díaz (escritora de libros infantiles), Inés Mármol (cantante de un grupo punk), Javier Fernández (cómico/guionista), Ramón Nogueras (activista climático), Daniel Pellicer (jugador profesional de golf), Pablo Tristán (cocinero de renombre), Alejandro Sánchez (violinista) y Maja Wrzeistein (profesora de literatura hispánica).
En los interrogatorios los sospechosos no saben precisar las fechas exactas en las que estuvieron en la casa de la fallecida, pero sí son capaces de describir claramente a los agentes con quienes coincidieron:
– Laura dice haber coincidido con Javier y con Maja.
– Inés aseguró haber visto a Ramón, Pablo y Daniel.
– Javier recuerda haber visto a Laura, Alejandro, Daniel y Ramón.
– Ramón comenta haber visto a Inés y a Javier.
– Daniel recuerda haber visto a mucha gente, concretamente a Javier, Alejandro, Pablo e Inés.
– Alejandro aseguró haber coincidido con Javier, Daniel, Pablo y Maja.
– Pablo dice haber visto sólo a Inés, Alejandro y Daniel.
– Maja comenta haber visto sólo a Laura y a Alejandro.
Los inspectores observan que las versiones de los sospechosos no presentan contradicciones y en principio no parece que nadie esté mintiendo, ¿o quizá sí?
Resolución del crimen
Dadas las declaraciones de los sospechosos sabemos con quien ha coincidido cada uno (o al menos lo que declaran). Esto nos permite realizar el grafo de intervalos correspondiente a la situación.
Por simplicidad denotaremos a cada sospechoso con la inicial de su nombre, es decir Laura (L), Inés (I), Javier (J), Ramón (R), Daniel (D), Alejandro (A), Pablo (P) y Maja (M).
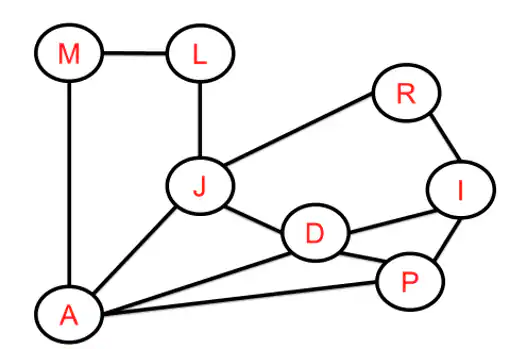
Ahora bien, recordemos que un grafo de intervalos siempre está triangulado, o equivalentemente, para todo camino cerrado (conjunto de aristas que comienza y acaba en un mismo vértice) formado por al menos cuatro aristas, existe una arista que une vértices no consecutivos.
Sin embargo, en nuestro grafo de intervalos (ver figura 5) tenemos un primer camino cerrado –el formado por A-M-L-J constituido por cuatro aristas y que no está triangulado.
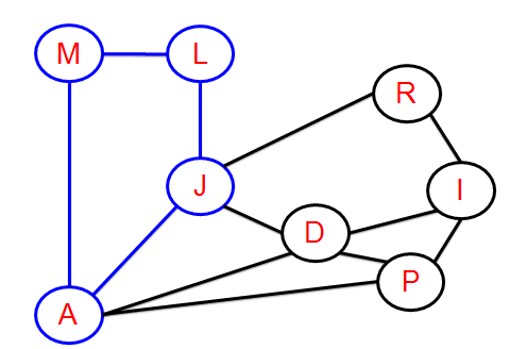
Así que hay alguien de ese subconjunto de sospechosos (Alejandro-Maja-Laura-Javier) que no está diciendo la verdad, ya que al tratarse de un grafo de intervalos éste debe estar triangulado. O lo que es lo mismo, o bien Alejandro y Laura han coincidido o bien lo han hecho Javier y Maja.
Por otra parte, observando nuestro grafo de intervalos (ver figura 6) podemos encontrar un segundo camino cerrado: el formado por J-R-I-D constituido por cuatro aristas y que no está triangulado.
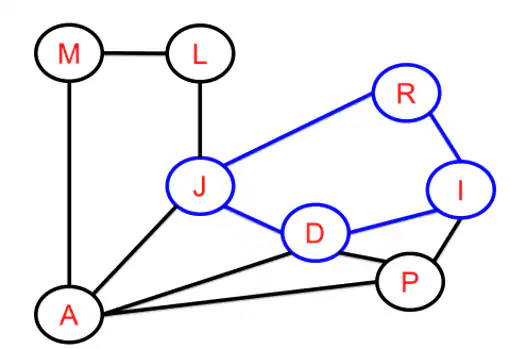
Así que alguien de ese nuevo subconjunto de sospechosos (Javier-Ramón-Inés-Daniel) está mintiendo ya que, de nuevo, al tratarse de un grafo de intervalos éste debe estar triangulado, o lo que es lo mismo: o bien Javier e Inés han coincidido o bien lo han hecho Ramón y Daniel.
Ahora bien, si tenemos en cuenta que tal y como se indicaba en la historia “las primeras pesquisas permiten a los agentes deducir que el crimen ha sido llevado a cabo por una única persona”, el único sospechoso que se encuentra en ambos subconjuntos de sospechosos es Javier el cual en verdad ha coincido en el pueblo con Inés y con Maja pero en esos momentos se encontraba oculto preparando su macabro plan, así que Javier Fernández (cómico/guionista) es el asesino.
Víctor M. Manero (@pitimanero) es profesor de la Universidad de Zaragoza y miembro de la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).
Fuente: abc.es, 31/01/22
.
.



Comentarios
Algo para decir?
Usted debe estar logueado para escribir un comentario.