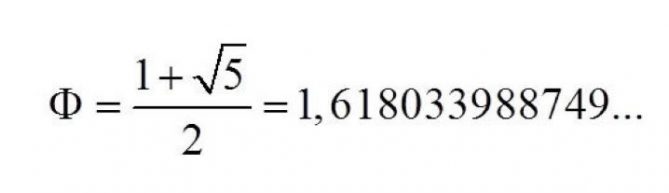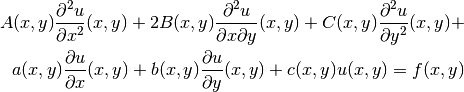Las matemáticas del Juego del Solitario
septiembre 5, 2024
Mucho más que un pasatiempo: las matemáticas del Solitario
Por Miguel Barral.
El juego del Solitario habría sido inventado por un aristócrata francés durante su encierro en La Bastilla. Eso cuentan algunas versiones sobre su origen, que se situaría en la primera mitad del siglo XVII —pues esa fue la época en la que el monarca Luis XIV empleó la fortaleza como prisión para los nobles que no le eran afines. Sea más o menos creíble, este legendario origen pone de manifiesto tanto la antigüedad como la naturaleza del juego: un pasatiempo sencillo, que se puede jugar en cualquier sitio y que permite matar las horas en soledad; y de ahí su atemporal popularidad y vigencia.

Pero no ha sido hasta finales de 2019, cuando por fin se ha logrado determinar la probabilidad de ganar una partida. Esta cuestión, que durante décadas había sido objeto de estudio por parte de aficionados y matemáticos, se ha resuelto recurriendo a un programa informático para poder abordar los complejos y laboriosos cálculos.
Al margen de historias y leyendas, la primera referencia documentada sobre el juego corresponde a un grabado francés que representa a Anne-Joulie de Rohan-Chabot (1648-1709), princesa de Soubise, jugando al solitario. Esto sustentaría otra versión diferente sobre su origen, que identifica al matemático francés Pelisson como su inventor para entretenimiento de Luis XIV, conocido como el Rey Sol. Sin embargo, tal y como se refleja en el grabado, el juego representado es una modalidad del Solitario conocida como Solitario Noble o del Noble (y en inglés como Peg Solitaire) que se juega sobre un tablero con clavijas; y que atendiendo a ello podría ser el precursor u origen del juego de cartas.
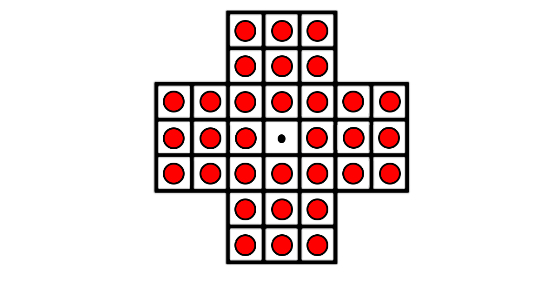
Pasatiempo 1:
El Solitario (del) noble se juega sobre un tablero, que en su versión más habitual tiene forma de cruz y 33 agujeros, con el central vacío y los restantes ocupados por piezas o clavijas. El objetivo es que solo quede una pieza ocupando la posición central.
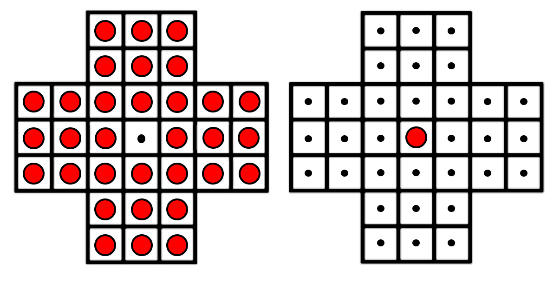
Para ello, el jugador debe ir eliminando clavijas una a una a base de saltar con una de ellas sobre otra —en horizontal o vertical— para ocupar un hueco libre. Tal que así:

A continuación se presentan dos configuraciones iniciales más sencillas. El reto es alcanzar el objetivo de que solo quede una clavija en la posición central:

nbsp;
EL SOLITARIO CON CARTAS
La modalidad jugada con cartas, que a la postre es la que ha acabado identificándose como Solitario, habría surgido a finales del siglo XVIII en los países bálticos como una forma de adivinación de la fortuna. Una hipótesis sustentada por el auge que en esa misma época experimentó la cartomancia y por el hecho de que en Escandinavia el juego era denominado Cabale, término que se ha vinculado a la Cábala judía.
Desde allí se habría extendido rápidamente al resto de Europa, tal y como atestigua que la primera referencia al término en el Oxford English Dictionary data de 1801. También que la primera obra conocida sobre el Solitario (una colección de juegos) apareciese publicada en Rusia en 1826; a la que poco después seguirían otras en Alemania y Francia. El juego se volvió tan popular que ya en sus Grandes Esperanzas (1864), Charles Dickens presenta a uno de los personajes jugando al Solitario.
Pasatiempo 2:
“Adivina” cuál es la carta que falta

Casi desde el mismo momento en que se popularizó, el Solitario concitó la atención de los matemáticos, que apoyados en la reciente rama de la Teoría de Juegos, trataron de determinar, entre otras cuestiones, la probabilidad de ganar una partida. Un cálculo que se les ha resistido desde entonces y que ha llegado a ser calificado como uno de los problemas más desconcertantes de las matemáticas.
Pasatiempo 3:
El Solitario danés es un juego o pasatiempo matemático en el que hay que colocar los naipes con valores del 1 al 10 en esta disposición:
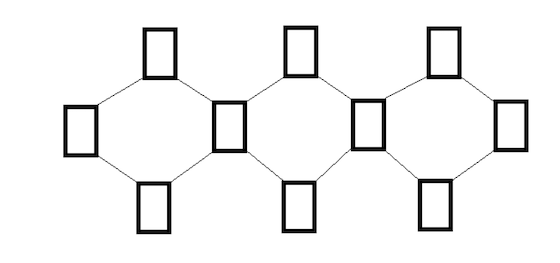
De tal modo que la suma de los cuatro naipes que conforman cada rombo y la suma de los cuatro naipes dispuestos en la fila central sea igual a 20, a 21, a 22, a 23 y a 24. ¿Cómo hay que colocarlos para que sumen 20 y 22?
EL PROGRAMA MÁS UTILIZADO DE MICROSOFT
A finales del s. XX el Solitario experimentó un nuevo e inesperado impulso con la aparición de los ordenadores personales. Y gracias en gran medida a Microsoft, que decidió incorporar el juego —en concreto, la modalidad conocida como Klondike— en el sistema operativo Windows 3.0 argumentando que se trataba de una forma amena e intuitiva de que el nuevo usuario se familiarizase con el manejo del ratón y de la interfaz gráfica. Desde entonces, no solo lo ha mantenido en todas las versiones posteriores de Windows, sino que ha introducido nuevas modalidades de juego en lo que constituye una apuesta segura ya que, según Microsoft, el Solitario es el más utilizado de sus programas, por delante incluso del Word y del Excel.
Ese “factor Microsoft” justifica que en el s. XXI el Klondike se haya convertido, con mucho, en la modalidad del Solitario más extendida y jugada. Y precisamente ha tenido que ser con el empleo de ordenadores (y en concreto con un programa de Inteligencia Artificial bautizado como Solvitaire) que se ha conseguido, por fin, establecer la probabilidad de ganar una partida para 45 modalidades diferentes del juego. Entre ellas, el Klondike, para el que el porcentaje de éxito se cifra en 81,96% ¿Será esta alta probabilidad de ganar otra de las claves de la popularidad del juego?
Pasatiempo 4
¿Una última partida al Solitario Noble? Como no podía ser de otra forma, ahora el reto es resolver la disposición usual, con 32 clavijas:


Pasatiempo 1:
Numerando las 33 posiciones del tablero de esta forma:

La solución para la configuración 1 es: 10-24, 15-17, 24-10, 19-17, 10-24.
Y para la 2: 10-02, 24-10, 19-17, 17- 05, 02-10, 15-17, 10-24, 29-17.
Pasatiempo 2:

El 3 de tréboles. En todas las filas la suma de las cartas impares es igual a la suma de las cartas pares. Y en cada fila se alinea una carta de cada palo.
Pasatiempo 3:
Pasatiempo 4:
Existen diversas soluciones, una de ellas es ésta:
05-17, 08-10, 01-09, 03-01, 16-04, 01-09, 28-16, 21-23, 07-21, 24-22, 21-23,26-24, 33-25, 31-33, 18-30, 33-25, 06-18, 13-11, 27-13, 10-12, 13-11, 24-26- 12-10, 10-08, 08-22, 22-24, 17-15, 29-17, 18-16, 15-17.
Miguel Barral está en Twitter (X): @migbarral
Fuente: bbvaopenmind.com
.
.
El gran misterio de las Matemáticas
agosto 5, 2024
Video (52′ 09»)
Documental que ofrece un maravillosos viaje de misterio matemático, una exploración del poder de las matemáticas a través de los siglos para descubrir su firma en la naturaleza, en el torbellino de una galaxia…
Fuente: Documentalia Ciencia, 2016.
Más información:
La belleza de las matemáticas
Borges y las Matemáticas
Libros para disfrutar las Matemáticas
Veinte matemáticos célebres
Los números en la naturaleza
Donald en el mundo de las Matemágicas
La importancia de las Matemáticas
Aquiles y la Tortuga
Matemáticas y juegos de azar
El arte matemático de Escher
Matemáticas: ¿descubrimiento o creación?
Martin Gardner, genio de las Matemáticas Recreativas
La Fascinante Curva Cicloide
julio 31, 2024
Por Gustavo Ibáñez Padilla.
En la enseñanza elemental se pone énfasis en las matemáticas como medio para ejercitar nuestra mente y desarrollar habilidades racionales. En geometría estudiamos el espacio plano y luego avanzamos al espacio de tres dimensiones. Nos familiarizamos con las rectas, los polígonos y los cuerpos. Dotados con estos conocimientos descubrimos que en la naturaleza abundan los círculos, cónicas, espirales, cardioides, catenarias, entre otras curvas, superficies y volúmenes.
Las curvas en las que la naturaleza ha desplegado su creatividad solo fueron apreciadas en toda su belleza matemática a partir del siglo XVIII, cuando se desarrolló el cálculo diferencial, una herramienta necesaria para explorar este maravilloso universo de formas.
La Cicloide, una curva singular
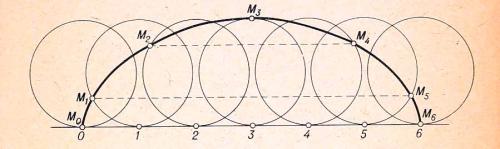
Si hacemos rodar un círculo sobre una superficie plana sin resbalar y observamos la trayectoria que dibuja un punto cualquiera del mismo, veremos que al principio se desplazará hacia arriba, alcanzará una altura máxima igual al diámetro del círculo, y luego descenderá hasta tocar la línea horizontal en un punto situado a una distancia del original igual a la circunferencia del círculo. A esta curva, que se repite continuamente, se la denomina cicloide. Es una curva con muchas particularidades que ha intrigado a los matemáticos durante siglos. La cicloide fue durante más de un siglo fuente de controversias y disputas entre los matemáticos.
Evangelista Torricelli (1608-1647), discípulo de Galileo Galilei, publicó un importante estudio en 1644 sobre la cicloide, que ya era estudiada durante años por su maestro.
.
Propiedades Tautócrona y Braquistócrona
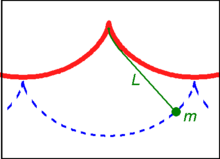
Una de las propiedades más notables de la cicloide es la tautócrona. Los científicos observaron que, despreciando el rozamiento, si invertimos una cicloide y dejamos caer un objeto por ella (como una pequeña esfera), llegará a la parte más baja en un tiempo que no depende del punto de partida. Esta propiedad se denomina tautócrona.
Otra característica fascinante de la cicloide es la braquistócrona. En esta curva, el tiempo de recorrido es menor que en un segmento recto, es decir, se minimiza el tiempo necesario para recorrer una distancia. Por esta razón, los toboganes de patinaje a menudo tienen forma de cicloide, para permitir que los patinadores lleguen abajo en el menor tiempo posible. Además, siguiendo el principio de Fermat, la trayectoria seguida por un haz de luz entre dos puntos es aquella que resulta en el menor tiempo de viaje, dibujando así una curva braquistócrona.
.
La Cicloide en la Vida Cotidiana
La cicloide no es solo una curiosidad matemática; sus aplicaciones prácticas son numerosas y variadas. Por ejemplo, los relojes de péndulo diseñados por Christiaan Huygens en el siglo XVII utilizaron la cicloide para mejorar la precisión del tiempo. Huygens demostró que un péndulo que oscila en un arco cicloidal tiene un periodo de oscilación constante, lo que no ocurre con un péndulo que oscila en un arco circular.
[La construcción del péndulo isócrono aprovecha una propiedad fundamental de la curva cicloide, que consiste en que su evoluta es otra cicloide. (La evoluta de una curva es la curva envolvente de la familia de rectas normales a la curva original en todos sus puntos, en el sentido de que dichas rectas normales son tangentes a la evoluta en puntos correspondientes.)]
.
Además, las cicloides se utilizan en el diseño de engranajes para maquinaria. Los engranajes cicloidales tienen ventajas sobre los engranajes tradicionales porque pueden reducir el desgaste y aumentar la eficiencia al distribuir la carga de manera más uniforme.
.
La Cicloide en la ciencia moderna
En el campo de la física, las cicloides también desempeñan un papel crucial. En la óptica, la trayectoria de la luz puede modelarse utilizando la curva cicloide para estudiar cómo los rayos de luz se comportan en diferentes medios. Esto tiene aplicaciones en el diseño de lentes y sistemas ópticos avanzados.
Asimismo, en la ingeniería civil, la forma cicloidal se utiliza en el diseño de puentes y arcos, ya que puede soportar mejor las cargas y distribuir las tensiones de manera eficiente. La naturaleza ha inspirado a los ingenieros a adoptar esta forma para construir estructuras más resistentes y duraderas.
.
Un legado duradero
La cicloide, con sus propiedades tautócrona y braquistócrona, ha dejado una huella profunda en el desarrollo de las matemáticas y la física. Su estudio no solo ha contribuido a nuestra comprensión de las curvas y sus propiedades, sino que también ha llevado a avances tecnológicos y científicos significativos.
En síntesis, la cicloide no es solo una curiosidad matemática, sino una herramienta fundamental en diversas áreas de la ciencia y la ingeniería. Su elegancia y utilidad nos recuerdan que, al igual que en la vida, las formas más bellas y eficientes no siempre son las más simples. La próxima vez que veas un tobogán, un reloj de péndulo o incluso una lente óptica, recuerda que detrás de su diseño hay una curva que ha fascinado a los matemáticos y científicos durante siglos. La cicloide es un testimonio del poder de la matemática para describir y mejorar el mundo que nos rodea.
Fuente: Ediciones EP, 2024.

Más información:
El Encanto Matemático: Un viaje revelador a través de Fibonacci y Zeckendorf
Medidas de Tendencia Central en el Mundo Financiero
La Regresión a la Media y la Ley de los Grandes Números: Su Impacto en las Finanzas y la Gestión del Riesgo
La importancia del Azar: Más allá de un juego de dados
Los números en la naturaleza
Donald en el mundo de las Matemágicas
Aquiles y la Tortuga
Matemáticas y juegos de azar
El arte matemático de Escher
.
.
El enigma resuelto por Euler que hoy nos permite acceder a Internet
julio 24, 2024
El enigma resuelto hace 300 años por el matemático Leonhard Euler que hoy nos permite acceder a Internet

.
El desafío matemático anual presentado por la Academia de Ciencias en París en 1727 fue este: «¿Cuál es la mejor manera de organizar mástiles en un barco?»
A primera vista es un problema muy práctico, pero el joven matemático suizo Leonhard Euler lo abordó como un rompecabezas puramente matemático.

Sello del año 1957 de la antigua Unión Soviética conmemorando el 250 aniversario del nacimiento de Euler.
A pesar de nunca haber puesto un pie a bordo de un barco, se sintió perfectamente calificado para calcular la disposición óptima de los mástiles.
Leonhard Euler tenía una fe absoluta en las matemáticas.
Legado que llega hasta hoy

.
Euler es uno de los matemáticos más prolíficos de todos los tiempos. ¡Hay tantas ideas matemáticas que llevan su nombre! 50 años después de su muerte, su trabajo aún se estaba publicando. Reformó casi todas las áreas de las matemáticas.
Y, como si fuera un hobby, resolvió el problema de los siete puentes de Königsberg, un popular enigma del siglo XVIII.
«Para Euler resolver el problema fue una forma de entretenimiento, era algo intrincado y ameno que hacer», le dijo a la BBC el experto en tecnología Bill Thompson.
«Por supuesto él no tenía idea de cuánto aprovecharíamos su trabajo, cómo construiríamos sobre sus ideas ni de que usaríamos lo que nos dejó para crear y ejecutar una red que ha cambiado el mundo por completo».
Se refiere a internet.
Para Euler fue solo un juego, pero las matemáticas que creó para resolverlo se usan para hacer que los motores de búsqueda sean mucho más eficientes.
Como respirar
Desde una edad temprana, Leonhard Euler «calculaba sin ningún esfuerzo aparente, así como los hombres respiran, como las águilas se sostienen en el aire», según el matemático francés François Arago.
Probaba teoremas por diversión, así como tú o yo podríamos hacer Sudoku. Pero su padre, que era clérigo, quería que siguiera sus pasos.
«Tuve que registrarme en la facultad de Teología, y debía aplicarme a los idiomas griego y hebreo, pero no progresé mucho, pues dedicaba la mayor parte de mi tiempo a estudios matemáticos, y para mi feliz fortuna, las visitas del sábado a Johann Bernoulli continuaron».
Johann Bernoulli fue un destacado matemático con sede en la ciudad natal de Euler, Basilea, donde en el siglo XVIII había una suerte de mafia matemática.
La familia Bernoulli produjo ocho matemáticos sobresalientes en solo cuatro generaciones.
Johann fue tutor de Euler y persuadió a su padre para que le permitiera estudiar matemáticas en vez de religión.
Y fue el hijo de Johann, Daniel, gran amigo de Euler, quien le encontró su primer empleo, en la Academia de San Petersburgo donde él trabajaba.
Era en la sección médica, lo cual no era ideal, pero antes de irse a Rusia, Euler leyó todo lo que pudo sobre medicina. Tal era su forma de pensar, que logró convertir la fisiología de la oreja en un problema matemático.
El día en que Euler llegó, Catalina I de Rusia, la gran patrona liberal de la Academia de San Petersburgo, murió.
En medio de la confusión, Euler se mudó discretamente de la sección médica al departamento de matemáticas y a nadie pareció importarle.
Cruzando puentes

.
Mientras estaba trabajando en San Petersburgo, Euler se enteró del conocido problema de los 7 puentes de Königsberg.
La ciudad prusiana de Königsberg estaba dividida en cuatro regiones distintas por las diversas ramas del río Pregel.
Siete puentes conectaban esas cuatro áreas diferentes y, en la época de Euler, se había convertido en un pasatiempo de tardes domingueras entre los residentes de la ciudad tratar de encontrar una manera de cruzar todos los puentes una sola vez y volver al punto de partida.

.
Euler le escribió una carta al Astrónomo de la Corte en Viena en 1736, describiendo lo que pensaba del problema:
«Esta pregunta es tan banal, pero me pareció digna de atención porque ni la geometría, ni el álgebra, ni siquiera el arte de contar era suficiente para resolverlo».
«En vista de esto, se me ocurrió preguntarme si pertenecía a la geometría de posición, que (el polímata alemán Gottfried Wilhelm von) Leibniz alguna vez tanto anheló.»
«Y así, después de un poco de deliberación, obtuve una regla simple, pero completamente establecida, con cuya ayuda uno puede decidir de inmediato, para todos los ejemplos de este tipo, si tal ida y vuelta es posible».
En lugar de caminar interminablemente por la ciudad probando diferentes rutas, Euler creó una nueva «geometría de posición«, en la cual las medidas anticuadas como longitudes y ángulos ?todas las medidas de hecho? eran irrelevantes.
La topología (análisis situs) estudia las propiedades geométricas que
son invariantes bajo deformaciones continuas.
Lo que importa es cómo están conectadas las cosas.
Euler decidió pensar en las diferentes regiones de tierra en Königsberg que estaban separadas por el río como puntos y los puentes que los unen, como líneas que los conectan.

.
Lo que descubrió es esto: para que un viaje de ida y vuelta (sin volver sobre tus pasos) sea posible, cada punto -excepto los puntos de inicio y final- debe tener un número par de líneas entrando y saliendo.
La ventaja de la regla de Euler es que funciona en cualquier situación.
Cuando analizó su mapa de los siete puentes de Königsberg de esta manera, descubrió que cada punto o pedazo de tierra tenía un número impar de líneas o puentes que emergían de ellas.
Así, sin tener que caminar una y otra vez por la ciudad, descubrió matemáticamente que no era posible caminar por la ciudad cruzando cada uno de los puentes una sola vez.
Del siglo XVIII al XXI
La regla de Euler es fácil de aplicar.
Lo difícil era enmarcar el problema del puente Königsberg de esa manera en primer lugar y así como probar que «la cantidad de líneas que entran y salen de cualquier punto» realmente es todo lo que necesitas saber para saber si ese viaje es posible o no.
Y no se necesita ser un matemático para que una idea como esta te sea útil.

.
La solución matemática de Euler al enigma de Königsberg ahora impulsa una de las redes más importantes del siglo XXI: internet, una red que conecta millones de computadoras en todo el mundo y mueve datos digitales entre ellos a una velocidad increíble.
«Si tengo mi computadora en casa y quiero entrar en un sitio web, necesito hacer una conexión entre mi computadora y el sitio web que puede estar en cualquier lado», dice Bill Thomson.
«Y puedo hacer esa conexión porque en mi computadora están incrustadas reglas basadas en el trabajo que Euler hizo en el siglo XVIII cuando trató de resolver el enigma de los puentes de Königsberg», explica el experto en tecnología.
El de los puentes de Königsberg estaba lejos de ser un problema acuciante en ese momento, más bien era una curiosidad, pero la solución de Euler perduró y revolucionó la era de la información del siglo XXI.
Lo que para Euler fue apenas un recreo, lanzó una de las ramas más importantes de las matemáticas.
Es como un cuento de hadas matemático, una historia con la que casi todos los matemáticos se criaron.
Fuente: La Nación, 12/05/18.
Vincúlese a nuestras Redes Sociales: LinkedIn YouTube Twitter
.
.
El Encanto Matemático: Un viaje revelador a través de Fibonacci y Zeckendorf
mayo 16, 2024
Por Gustavo Ibáñez Padilla.
En el complejo y misterioso mundo de las matemáticas, hay ciertos fenómenos que capturan en forma inmediata la imaginación del público en general. Uno de esos enigmas fascinantes es la relación entre la Sucesión de Fibonacci y el Teorema de Zeckendorf. ¿Qué tienen en común estas dos joyas matemáticas? ¿Y por qué nos siguen sorprendiendo hasta el día de hoy? Lo veremos a continuación.
La sucesión de Fibonacci es, sin duda, una de las secuencias más famosas en el mundo de las matemáticas. Comienza con los números 0 y 1, y cada número subsiguiente es la suma de los dos anteriores. Así, la secuencia resulta ser: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, y así sucesivamente hasta el infinito. Esta secuencia aparentemente simple ha fascinado a matemáticos, artistas e incluso biólogos debido a su aparición en una enorme variedad de fenómenos naturales, desde la disposición de las hojas en una rama hasta los patrones de crecimiento de los girasoles.
La historia de la sucesión de Fibonacci se remonta al siglo XIII, a un hombre conocido como Leonardo de Pisa, comúnmente llamado Fibonacci. En su influyente libro Liber Abaci, publicado en 1202, Fibonacci presentó al mundo occidental los números indo-arábigos y sus aplicaciones en la aritmética. Pero lo que llamó la atención de muchos fue un problema aparentemente simple sobre el crecimiento de una población de conejos, que llevó al descubrimiento de la secuencia de números que ahora lleva su nombre.
¿Cuál es la relación de Fibonacci con el teorema de Zeckendorf? Pues que este teorema afirma que: Todo entero positivo se escribe, de manera única, como suma de números de Fibonacci no consecutivos. A esa escritura única se le llama la descomposición de Zeckendorf del número en cuestión.
Así pues, todos los números naturales pueden expresarse como la suma de números de Fibonacci únicos. Es decir, cada número natural puede descomponerse de manera única como una suma de números de Fibonacci, sin que ninguno de ellos se repita. Esta descomposición única es lo que hace que el teorema de Zeckendorf sea tan intrigante, ya que revela una estructura ordenada y predecible que ha fascinado a generaciones de matemáticos. ( Por ejemplo: 10= 2+8 ; 26 = 5+21 ; 43 = 1+8+34 )
El matemático francés Édouard Lucas, famoso por su trabajo en Teoría de números y sus libros de matemáticas recreativas, manifestó: “Los números de Fibonacci son como un gran cuento, lleno de sorpresas y misterios, esperando ser descubiertos”. Fue Lucas quien le puso el nombre a esta famosa sucesión, de la cual descubrió numerosas características, desde patrones geométricos hasta propiedades únicas en teoría de números.
Una de las sorpresas más asombrosas de este universo matemático es la relación entre la sucesión de Fibonacci y la proporción áurea representada por el número φ (phi), cuyo valor es aproximadamente igual a 1,618, un número misterioso que parece resonar en los rincones más profundos de la naturaleza y el arte. Como si estuvieran bailando al unísono, los números de Fibonacci revelan una conexión íntima con esta proporción divina a medida que crecen hacia el infinito, como si estuvieran siguiendo una partitura escrita en el corazón mismo de la realidad.
“Las matemáticas son la poesía del universo”, sostuvo el genial matemático David Hilbert, y en la intersección de Fibonacci y Zeckendorf, encontramos una poesía matemática que cautiva y encanta con su elegancia y misterio.
Estas sorprendentes relaciones e intersecciones entre diversos conceptos matemáticos son las que nos llevan a afirmar que las matemáticas son una verdadera unidad, lo cual llevo también a los ’modernos’ a denominarla en singular y con mayúscula, como Matemática.
“Los números de Fibonacci son como una sinfonía matemática, cada uno tocando su propia melodía única, pero juntos creando una armonía incomparable” afirmaba Lucas. ¿Qué papel desempeña el teorema de Zeckendorf en esta sinfonía matemática? Resulta que este teorema proporciona un marco ordenado y estructurado para entender cómo los números naturales se descomponen en términos de números de Fibonacci únicos. Es como si cada número natural tuviera una historia que contar, una historia que se revela a través de su descomposición en términos de esta antigua secuencia numérica.
“Las matemáticas son el arte de dar el mismo nombre a diferentes cosas”, dijo el matemático francés Henri Poincaré, y resulta evidente en la intersección de Fibonacci y Zeckendorf. A través de estas ideas aparentemente abstractas, descubrimos un mundo rico y vibrante de posibilidades matemáticas que nos desafían a mirar más allá de la superficie y explorar las profundidades del universo numérico.
Pero la diversión matemática no se detiene aquí. El teorema de Zeckendorf ha inspirado una serie de acertijos y juegos matemáticos que desafían la mente y estimulan el pensamiento creativo. Desde rompecabezas de descomposición de números hasta juegos de estrategia basados en la sucesión de Fibonacci, hay un mundo de aventuras matemáticas esperando ser exploradas por aquellos dispuestos a sumergirse en sus misterios.
Y no debemos olvidar el encanto de la matemagia, un arte que combina ilusionismo y matemáticas para crear asombrosos trucos de números y acertijos. Maestros de la matemagia como Sam Lloyd y Henry Dudeney han seducido audiencias con sus trucos ingeniosos basados en principios matemáticos, recordándonos que las matemáticas pueden ser tanto sorprendentes como entretenidas, como bien lo explica Martin Gardner en su libro Matematica, magia y misterio.
La Sucesión de Fibonacci y el Teorema de Zeckendorf nos invitan a un viaje fascinante a través del rico y sorprendente mundo de las matemáticas. Desde su aparición en la naturaleza hasta su aplicación en la teoría de números y los juegos matemáticos, estas ideas continúan maravillando y deleitando a quienes se aventuran en el emocionante viaje de descubrimiento matemático.
En palabras del prolífico matemático Paul Erdős: “Las matemáticas son como una aventura sin fin, siempre hay nuevas maravillas por descubrir”. Y en el universo de las matemáticas recreativas Fibonacci, Zeckendorf y sus seguidores están siempre listos para sorprender y extasiar a aquellos que se atreven a adentrarse en sus misterios.
Fuente: Ediciones EP, 16/05/24.
Información sobre Gustavo Ibáñez Padilla
Este artículo también ha sido publicado en Mendoza Today

Más información:
Los números en la naturaleza
Matemáticas: ¿descubrimiento o creación?
La importancia del Azar: Más allá de un juego de dados
.
.
La importancia del Azar: Más allá de un juego de dados
noviembre 17, 2023
Por Gustavo Ibáñez Padilla.
Álea iacta est – la suerte está echada. Estas palabras, atribuidas a Julio César en el crucial momento en que cruzó el río Rubicón, resonaron a lo largo de la historia como un recordatorio de que la vida está impregnada de elementos impredecibles. Hoy, en el siglo XXI, el concepto de azar cobra especial relevancia, por lo que resulta de gran interés explorar su papel en nuestras decisiones y considerar su presencia constante en eventos aparentemente insignificantes.
.
La aleatoriedad, definida como la imprevisibilidad inherente a ciertos eventos, procesos o modelos, encuentra su lugar en diversas disciplinas, desde las matemáticas hasta la filosofía y la física cuántica. En el vasto tablero de la existencia, cada lanzamiento de dados representa un encuentro con lo incierto.
En el ámbito matemático, se plantea una interesante paradoja: solo una secuencia infinita puede considerarse verdaderamente aleatoria. Para secuencias finitas, la influencia de un determinismo subyacente se hace evidente, ya que siempre es posible encontrar una fórmula que las reproduzca. Sin embargo, en la física cuántica, se postula una aleatoriedad profunda, desafiando nuestra capacidad de prever los resultados incluso en eventos macroscópicos como el lanzamiento de dados.
Blaise Pascal, Pierre de Fermat, Christiaan Huygens y Jacob Bernoulli, pioneros en la exploración de la probabilidad, sentaron las bases de lo que hoy conocemos como Teoría de Probabilidad. Estos visionarios matemáticos avanzaron en la comprensión de la aleatoriedad estadística, considerando las frecuencias de bloque como medida de lo impredecible.
.
La historia de la aleatoriedad se entrelaza con la eterna disyuntiva entre el libre albedrío y el determinismo. A lo largo de milenios, la filosofía y la teología han debatido sobre la autonomía de nuestras decisiones frente a un destino predestinado. Es en este diálogo entre lo impredecible y lo inevitable donde la aleatoriedad ocupa un papel crucial.
El término ‘aleatorio’ no solo denota la carencia de propósito, causa u orden, sino que también se asocia con propiedades estadísticas medibles, como la ausencia de tendencias o correlaciones identificables. En este sentido, la aleatoriedad se manifiesta como un fenómeno que trasciende la casualidad, influenciando tanto la ciencia como la historia.
A medida que avanzamos en la comprensión de la aleatoriedad, la Teoría de la información introduce la entropía como una medida de desorden, y los matemáticos Gregory Chaitin, Andréi Kolmogórov y Ray Solomonoff aportan la noción de aleatoriedad algorítmica. En este enfoque, la imprevisibilidad de una secuencia se relaciona con su capacidad para resistir la compresión algorítmica, desafiando la idea de un universo regido por patrones predefinidos. A pesar de ello cabe aquí recordar la frase del genial Albert Einstein: “Dios no juega a los dados”.
.
Pero, ¿cómo afecta el azar a nuestras vidas cotidianas? En situaciones aparentemente mundanas, como elegir una ruta para el trabajo o decidir qué película ver, la aleatoriedad se manifiesta. Tomemos el ejemplo de las aplicaciones de navegación: cada vez que confiamos en ellas para dirigirnos, confiamos en algoritmos que incorporan elementos de azar en la búsqueda de la ruta más eficiente. Detrás de la aparente simplicidad de estas decisiones se encuentra la complejidad de lo impredecible.
Incluso en la toma de decisiones más trascendentales, como elegir una carrera o a la pareja de vida, la influencia del azar no puede subestimarse. La vida está llena de giros inesperados, encuentros fortuitos y oportunidades que surgen sin previo aviso. En palabras de Nassim Taleb, autor de El Cisne Negro, la vida está llena de eventos altamente improbables que desafían nuestras expectativas y definen nuestro destino.
.
En última instancia, la importancia del azar en nuestra vida radica en su capacidad para desafiar nuestras certezas y abrir puertas a lo inexplorado. Al reconocer la presencia constante de la aleatoriedad, podemos abrazar la incertidumbre como parte integral de nuestra existencia. Cada paso que damos, cada decisión que tomamos, se convierte en una apuesta contra las probabilidades, recordándonos que, al igual que Julio César al cruzar el Rubicón, estamos echando el dado de la vida.
En un mundo cada vez más complejo e interconectado, la comprensión de la aleatoriedad se convierte en una herramienta invaluable. Nos permite adaptarnos a lo inesperado, encontrar oportunidades en los desafíos y abrazar la diversidad de experiencias que la vida tiene para ofrecer. En última instancia, la suerte puede estar echada, pero cómo enfrentamos la incertidumbre y aprovechamos las oportunidades que se presentan es el verdadero juego que define nuestra historia.
Fuente: Ediciones EP, 17/11/23.
Información sobre Gustavo Ibáñez Padilla
Más información:
Matemáticas y juegos de azar
Medidas de Tendencia Central en el Mundo Financiero
La Regresión a la Media y la Ley de los Grandes Números: Su Impacto en las Finanzas y la Gestión del Riesgo
.
.
La Regresión a la Media y la Ley de los Grandes Números: Su Impacto en las Finanzas y la Gestión del Riesgo
octubre 13, 2023
Por Gustavo Ibáñez Padilla.
En el complejo universo de las finanzas e inversiones, comprender las sutilezas estadísticas es crucial para tomar decisiones acertadas. Dos conceptos fundamentales que destacan en este panorama son la Regresión a la Media y la Ley de los Grandes Números, principios respaldados por la experiencia de matemáticos, expertos y empresarios de renombre. Reflexionaremos más a fondo en estos conceptos y su aplicación en finanzas, inversión y, crucialmente, en la Gestión del Riesgo y los Seguros, resaltando así la importancia de la Protección Financiera en la vida de todo empresario o inversor.
Regresión a la Media
La Regresión a la Media, propuesta por el visionario Francis Galton, nos recuerda que los resultados extremos tienden a equilibrarse con el tiempo. Esto tiene una aplicación vital en la Gestión del Riesgo y los Seguros. En palabras de Nassim Taleb, el reconocido autor de El Cisne Negro: “La Regresión a la Media es el alma de la gestión del riesgo.”
Supongamos un empresario que dirige una cadena de restaurantes. Después de un año excepcionalmente rentable, es sabio no asumir que este nivel de ganancias continuará indefinidamente. La Regresión a la Media sugiere que es más probable que las ganancias se estabilicen o disminuyan en el próximo período contable. Aquí, la Protección Financiera, en forma de reservas o seguros empresariales, puede ser la diferencia entre la continuidad del negocio y la crisis financiera ante una caída inesperada en las ganancias.
“Entender la Regresión a la Media es crucial para gestionar el riesgo. Es la base de cualquier sistema de seguro o protección financiera” nos recuerda el matemático y bróker de inversionesNassim Taleb.
Ley de los Grandes Números
La Ley de los Grandes Números ─formulada por el genial matemático suizo Jakob Bernoulli, en su obra Ars Conjectandi del siglo XVIII─ establece que a medida que se realizan un número creciente de experimentos o eventos independientes, la media de los resultados se aproximará al valor esperado o teórico. Esta ley es esencial para comprender cómo los resultados a corto plazo pueden variar significativamente de las tendencias a largo plazo.
.
Imaginemos un fondo de inversión que invierte en una amplia variedad de activos. Durante un trimestre, algunos activos pueden experimentar pérdidas, pero la cartera en su conjunto tiene una tendencia positiva. La Ley de los Grandes Números nos asegura que, a medida que se acumulan más trimestres, la rentabilidad promedio de la cartera se aproximará a la expectativa teórica.
El meollo de la cuestión se sintetiza en la siguiente afirmación de Jakob Bernoulli: “La aritmética de los acontecimientos inciertos es tan exacta como la de la certeza.”
La Ley de los Grandes Números es también el pilar de la industria de los Seguros. A medida que la cartera de asegurados se amplía, las compañías aseguradoras pueden prever con mayor precisión los eventos y establecer primas adecuadas.
Consideremos una compañía de seguros de salud. Al tener un gran número de asegurados, la compañía puede prever con alta certeza la cantidad de reclamaciones médicas que recibirán en un periodo determinado. Esto les permite fijar primas que cubran los costos, generando así beneficios tanto para la compañía como para los asegurados.
La certeza que nos brinda esta ley es refrendada por Warren Buffett, cuando dice: “La Ley de los Grandes Números es el fundamento de la industria de seguros. Nos permite entender y gestionar el riesgo.”
.
Aplicaciones en el Mundo de las Inversiones
Estos conceptos tienen un impacto sustancial en las decisiones de inversión y gestión de carteras:
- Selección de Activos: La Regresión a la Media advierte a los inversores sobre la posible reversión de tendencias extremas en el corto plazo.
- Diversificación y Gestión del Riesgo: La Ley de los Grandes Números respalda la estrategia de diversificación como una forma efectiva de mitigar el riesgo.
- Planificación a Largo Plazo: Ambos conceptos son esenciales para la toma de decisiones a largo plazo, permitiendo a los inversores evitar reacciones impulsivas a fluctuaciones temporales.
Especulación y Protección Financiera
Los especuladores exitosos, como George Soros, reconocen la importancia de la Protección Financiera. Soros, famoso por su papel en la caída de la libra esterlina en 1992, no solo especuló, sino que también utilizó estrategias de protección para mitigar el riesgo asociado con sus posiciones.
Imaginemos a un inversor que ha identificado una oportunidad de inversión en una nueva empresa tecnológica. Si bien está entusiasmado con el potencial de crecimiento, también es consciente de los riesgos inherentes a las startups. Aquí, la adopción de estrategias de Protección Financiera, como la diversificación de la cartera, puede ser crucial para mitigar el riesgo asociado con este tipo de inversiones más volátiles.
Siempre debemos recordar la recomendación de Nassim Taleb: “La Protección Financiera no es solo una estrategia, es una filosofía de vida. Permite a los inversores prosperar en la incertidumbre.”
Regresión a la Media y Ley de los Grandes Números como bases del éxito
La combinación de la Regresión a la Media y la Ley de los Grandes Números forma la base de decisiones financieras informadas y la gestión eficaz del riesgo. En un mundo mundo Volátil, Incierto, Complejo y Ambiguo, la Protección Financiera se convierte en una herramienta invaluable para asegurar la continuidad y el éxito en cualquier empresa o cartera de inversión. Como afirmó Warren Buffett, “la inversión exitosa es sobre la gestión del riesgo, no su eliminación.”
Al comprender y aplicar estos fundamentales conceptos, los empresarios, los inversores, los gestores de riesgos y las personas en general pueden desempeñarse con confianza en el cambiante escenario financiero, construyendo un futuro económico de mayor estabilidad y prosperidad.
Fuente: Ediciones EP, octubre 2023.
Información sobre Gustavo Ibáñez Padilla
Más información:
Medidas de Tendencia Central en el Mundo Financiero
.
.
Medidas de Tendencia Central en el Mundo Financiero
octubre 12, 2023
Por Gustavo Ibáñez Padilla.
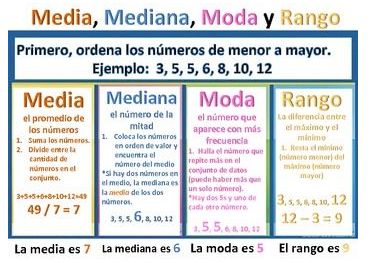
En el dinámico mundo de las finanzas, la clave para tomar decisiones acertadas radica en la capacidad de interpretar y analizar datos de manera rápida y efectiva. En este sentido, las Medidas de tendencia central estadística son herramientas fundamentales. La media, mediana, moda y rango son como brújulas que nos orientan en el vasto océano de la información financiera. Son parámetros estadísticos simples que indican cuál es el centro de un conjunto de datos. Su uso está muy difundido, ya que al resumir un conjunto de datos en un solo valor simplifican el análisis de todo un bloque de información y proporcionan una visión generalizada sobre el mismo.
.
Principales medidas de tendencia central
─La Media: Equilibrio en los Ingresos
La media, también conocida como promedio, es el punto de equilibrio de un conjunto de datos. Es el resultado de sumar todos los valores y luego dividirlos por la cantidad de elementos. Para visualizarlo, imaginemos un grupo de diez profesionales con diferentes niveles de ingresos. Si sumamos todos los sueldos y los dividimos entre diez, obtendremos la media de ingresos del grupo.
Es importante tener en cuenta que la media puede ser influenciada por valores extremos. Si uno de los profesionales tiene un sueldo excepcionalmente alto, este valor puede distorsionar la media y no reflejar la situación financiera real del grupo en su conjunto.
─La Mediana: Estabilidad en los ingresos
A diferencia de la media, la mediana es el valor intermedio de un grupo de números. Se trata del valor que se encuentra en el centro de un conjunto de datos ordenados. Imaginemos un grupo de nueve ejecutivos, esta vez ordenados por sus ingresos de menor a mayor. La mediana será el sueldo del quinto profesional en esta lista.
Lo destacado de la mediana es su resistencia a los valores atípicos. Esto la convierte en una herramienta valiosa para evaluar la estabilidad financiera del grupo. Si uno de los profesionales tiene un ingreso muy alto o muy bajo, la mediana no se ve afectada en la misma medida que la media.
─La Moda: El Favorito en los ingresos
La moda es el valor más frecuente en un conjunto de datos. Es como el favorito de la multitud. Siguiendo con el ejemplo de los ingresos, si cierto sueldo es el más repetido en el grupo de profesionales, entonces ese valor es la moda.
Para ilustrar este punto, imaginemos que en el grupo de diez ejecutivos, cinco de ellos tienen el mismo sueldo mensual. En este caso, ese sueldo específico se convierte en la moda. Esto puede indicar tendencias en los salarios de la industria o en la empresa en la que trabajan.
─El Rango: Variedad en los ingresos
El rango es la diferencia entre el valor más alto y el más bajo en un conjunto de datos. Nos brinda una visión clara de la variedad de resultados posibles. Continuando con el ejemplo de los profesionales, si el ingreso más alto es de U$S100.000 y el más bajo es de U$S30.000, el rango sería de U$S70.000. Esto nos indica que existe una amplia gama de ingresos en el grupo.
En el mundo financiero, el rango es una herramienta esencial para evaluar la volatilidad y el nivel de riesgo asociado a ciertos activos o inversiones. Un rango amplio sugiere una mayor variabilidad en los resultados y, por lo tanto, un mayor nivel de riesgo.
.
El valor de las medidas de tendencia central
Para respaldar la importancia de estos parámetros, el matemático John Allen Paulos señaló: «En un mundo inundado de datos, las medidas de tendencia central son faros que nos guían hacia decisiones más certeras.»
El famoso economista John Maynard Keynes también subrayó la relevancia de estas herramientas al afirmar: «Sin una comprensión profunda de las tendencias centrales de los datos, las decisiones económicas carecen de fundamento sólido.»
Tomando el timón de tus finanzas
Al aplicar estas medidas de tendencia central en el mundo financiero, te empoderas para tomar decisiones más inteligentes y adaptativas. Imagina que estás considerando invertir en dos fondos mutuos. Al analizar sus historiales de rendimiento, puedes usar la mediana para evaluar la estabilidad y la moda para identificar cuál ha sido el favorito del mercado. El rango te proporciona información sobre la variabilidad y el riesgo asociado a cada fondo.
En última instancia, al comprender y aplicar estas herramientas, estás tomando el timón de tus finanzas. No te limitas a navegar por el mar de datos, sino que tienes el poder de dirigir tu curso hacia un futuro financiero más próspero y seguro. Como dijo Martin Gardner, «la comprensión de las tendencias centrales nos brinda una brújula confiable en el laberinto de la información financiera.» ¡Así que adelante, fija el rumbo y emprende tu ruta hacia el éxito financiero!
Fuente: Ediciones EP, 11/10/23.
.
.
La utilidad de la Historia
octubre 2, 2023
¿La Historia es una ciencia?
Se sabe que, en Historia, es prácticamente imposible obtener teorías o leyes generales de forma deductiva y más tarde soportar un experimento como sucede en las ciencias sociales, pues lo histórico viene ya de experiencias vividas, de observaciones a lo largo del tiempo. ¿Qué experimentación habrían de precisar?
Desde luego que ninguna. La Historia, como tal, es una ciencia social en la que intervienen infinidad de variables y donde las constantes pueden cambiar con facilidad; por lo tanto, bajo esa perspectiva, es difícil elaborar leyes generales tal como lo entiende la comunidad científica y muchos pensadores.
Las proporciones científicas
Pero, ¿qué entendemos por teorías o leyes generales? Podría valernos el considerarlas como un conjunto de supuestos a partir de los cuales, mediante razonamientos lógicos, sería posible deducir hechos, sucesos o acontecimientos del tipo de:
“identificada científicamente una cosa, situación o proporción, mediante cálculos aritméticos o razonamientos lógicos, deducimos o predecimos otra, o sea: (A) mediante (r), se convierte en (B)”.
Por ejemplo, en la ciencia natural por antonomasia, que es la física newtoniana, el espacio recorrido por un cuerpo es igual a la velocidad que lleva ese cuerpo, multiplicado por el tiempo que tarda en recorrerlo (E = V x T); o, en la ley de la palanca, donde Potencia por su brazo es igual a la Resistencia por el suyo (P x b1 = R x b2).

Todo ello ¿Qué nos está diciendo? Bajo mi punto de vista lo que nos están diciendo todas estas fórmulas o ecuaciones es que existen unas proporciones, unas equivalencias entre las partes y el todo; por ejemplo, entre velocidad y tiempo con el espacio, y también entre las partes, o sea, entre velocidad y tiempo entre sí.
En el segundo ejemplo, se podría decir que existe una proporción o correspondencia máxima -que llega a la igualdad- entre dos elementos, aparentemente distintos, que son los dos miembros de la ecuación, (P x b1) por un lado y (R x b2) por el otro; de tal forma que si al primer miembro lo llamamos (A) y al segundo miembro lo llamamos (B), A : B = 1, o lo que es lo mismo, la proporcionalidad mínima o máxima, según se mire, es la igualdad, y a partir de ese punto diremos que un elemento es poco o muy proporcional a otro.
Puede ser directamente proporcional, en razón de sus magnitudes, de forma que cualquier cambio del primer elemento produce un cambio cuantitativo o cualitativo del segundo en el mismo sentido; e inversamente proporcional, de forma que cualquier cambio del primer elemento origina un cambio del segundo, pero en sentido inverso.
Las proporciones de los hechos históricos
El análisis anterior nos sirve para despejar dudas y tener un punto de partida no “contaminado” de la gran cantidad de fórmulas, modelos y opiniones que existen sobre el particular, y que nos llevan a afirmar que, en cualquier teoría o ley general, existen proporcionalidades entre los diferentes elementos, sucesos, hechos, fenómenos…
Y en la Historia y las ciencias sociales se pueden encontrar proporcionalidades, relaciones y análisis entre muchos de sus elementos, sucesos, hechos y fenómenos, como sucede en las ciencias naturales. La cuestión es que las matemáticas y la física necesitan proporciones máximas y no se conforman con proporciones menores, es decir, las matemáticas y la física no pueden permitirse el más mínimo error en la mayoría de los casos, y por ello buscan teorías que se puedan plasmar en igualdades y ecuaciones, pero las ciencias sociales, y en especial la Historia, no precisan tanto, se conforman con encontrar regularidades y analogías.

Carl G. Hempel afirma en su obra La explicación científica, que sería más correcto hablar de “hipótesis universales” en lugar de hacerlo de “leyes generales”, y que buscar una “hipótesis universal” en la Historia debería hacerse bajo el presupuesto de hallar una hipótesis que afirme una regularidad del siguiente tipo:
“en todos los casos en donde un hecho de una clase específica C ocurre en un cierto lugar y tiempo, otro hecho de una clase específica E ocurrirá en un lugar y tiempo relacionados de un modo específico con el lugar y el tiempo de ocurrencia del primer suceso.”
Simetrías y semejanzas
El modelo de hipótesis de Hempel hace que me sienta cómodo, sobre todo, porque es el modelo más común que aparecerá casi siempre en cualquier hipótesis histórica que se quiera formular, al incorporar dos factores fundamentales de la historia: espacio y tiempo, sin los cuales la historia no tendría sentido.
Sin embargo, lo que la Historia no puede establecer es “en todos los casos”, y, en ese sentido, la Historia no puede ni debe pretender ser una ciencia que pueda crear modelos matemáticos de ecuaciones e igualdades, ni tampoco establecer una “ley general” que pueda ser refutada por motivo de una sola predicción que no se cumpla, como afirman los racionalistas con Karl Popper a la cabeza.
Mi opinión es que, a la Historia le basta con establecer proporcionalidades y analogías entre hechos, elementos, sucesos o acontecimientos del pasado con respecto al presente, y que, gracias al modelo inductivo –el mejor por ser histórico–, se puedan predecir tendencias futuras e incluso, utilizando la estadística, analogías y semejanzas.
Resumiendo, las ciencias exactas precisarán ecuaciones algebraicas para establecer la “ley general”, y las ciencias naturales precisarán experimentaciones científicas rigurosas o demostraciones algebraicas para ser aceptadas; en cambio, las ciencias sociales se conforman con “esbozos de ley general” o proporcionalidades.
En palabras más sencillas, las ciencias exactas se identifican con igualdades; las ciencias naturales se identifican con igualdades fiables, es decir, sometidas a refutación experimental; y las ciencias sociales establecen proporcionalidades y analogías a través de series de hechos similares comprobados, que darían origen a un sistema de probabilidades que pudiera establecer una “ley general”.
En ese sentido, la Historia sería la ciencia más adecuada y fiable para poder establecer hipótesis del tipo inductivo, ya que los (n) elementos, hechos, sucesos o acontecimientos que puede presentar como prototipos, son de una gran seguridad y solvencia al tratarse de elementos, hechos, sucesos o acontecimientos históricos, teniendo, además, como elemento catalizador al tiempo, que es consustancial con la Historia y fundamental a la hora de valorar si un determinado suceso está sometido o no a una ley general; es decir, se puede someter a una ley general válida, y se puede estudiar y analizar bajo el punto de vista de las ciencias naturales o, por el contrario, es un suceso singular que se deberá estudiar y analizar bajo el prisma de las ciencias humanas o del espíritu; o sea, nosotros opinamos con convicción que muchos sucesos históricos podrían estar sometidos a leyes generales para pequeños periodos de tiempo, y, por otro lado, también estamos convencidos de que muchas leyes generales establecidas desde las ciencias naturales en un tiempo ilimitado, podrían no tener validez.
Leyes naturales y leyes sociológicas
Consideremos un ejemplo. Históricamente, está constatado que, en una amplia sociedad, cuanto más se incrementa la clase media menos posibilidades hay de que haya grandes revoluciones. Llamando a la sociedad A y a la clase media B, se producirá que, a medida que la clase media aumenta, el riesgo de revolución R disminuye convirtiéndose en R’, siendo B y R cuantificable en número, cantidad o dimensión. Contrariamente, a medida que la clase media disminuye, el riesgo de revolución aumenta; por lo tanto, creemos que existe una proporcionalidad que se puede constatar históricamente, pero que no podemos asegurar que se cumplirá siempre y en cualquier lugar.
Sin embargo, sí se producirá una cuasi igualdad en forma de ecuación que diga: en una sociedad de ciertas dimensiones A, y en tiempo (t) suficientemente pequeño: B’ / B = R / R’, de tal forma que, cuando en la sociedad A, con una clase media B, y en un tiempo muy corto, a medida que aumenta la clase media disminuirán las revoluciones, ya sea en cantidad o intensidad.
Cierto es que no podemos estar seguros de que esa igualdad se seguirá produciendo en el futuro, puesto que la ecuación nace de una inducción histórica y, bajo el punto de vista de las ciencias naturales, nadie puede asegurar que esa ley se siga produciendo en un tiempo futuro ilimitado, pero existen una serie de elementos psicológicos y sociológicos de la sociedad que aseveran que es más fácil que una sociedad se revele violentamente contra el orden establecido y las instituciones cuando esa sociedad está formada por una mayoría de clase baja, que si está formada por una mayoría de clase media.
Resumiendo, podemos afirmar que, en un tiempo corto, muchas leyes inductivas serían tan válidas como las leyes deductivas y, por consiguiente, podemos afirmar que, en el corto plazo, existen muchas generalidades de carácter histórico que se podrían emplear discretamente para conocer mejor el pasado, y prevenir cuidadosamente el futuro, o lo que es lo mismo: las aproximaciones y tendencias, en el corto plazo, pueden tener validez para la historia.
El continuo e infinito tiempo
Nuestro punto de vista sobre el tiempo es el siguiente:
El tiempo podría ser relativo para cada Sistema, partiendo de una unidad global que es el mundo, como el conjunto de galaxias; nuestro mundo correspondería a la constelación de la Vía Láctea y la Tierra, donde vive la humanidad, gira alrededor de una estrella incandescente llamada Sol, que es de donde recibe el calor para producir y mantener a los seres vivientes del planeta Tierra, y, por ende, la vida del ser humano.

Pues bien, dejando de lado el tiempo de esa unidad global del Mundo, nuestro tiempo será la magnitud que mide los procesos de rotación y traslación de la Tierra alrededor del Sol, pero si hacemos un esfuerzo de abstracción mental o, como dirían Horkheimer y Adorno, “logramos separar el sujeto del objeto mediante un esfuerzo mental” al mismo tiempo que nos olvidamos del día, de la noche, de los relojes…, ¿qué sería el tiempo para nosotros? ¿No sería algo vacío, solo medible por el envejecimiento de nuestro cuerpo, el crecimiento de plantas, el nacimiento de criaturas, su crecimiento o el deterioro de las cosas que nos rodean?
Por lo tanto, nosotros creemos que el tiempo siempre está ligado a “acción” y movimiento, y lo que el ser humano identifica como tiempo en realidad es duración, cosa que ya Bergson lo afirmaba en su obra La Evolución Creadora, donde asevera que nuestra inteligencia tiende a considerar el tiempo de una forma rectilínea y distingue de modo artificial el pasado, presente y futuro, mientras que, para la auténtica realidad de la conciencia, el tiempo es duración (durée), o sea, algo no susceptible de reducirse a un instante, porque es un flujo continuo “cuyos momentos sucesivos no pueden separarse”. Por consiguiente, la duración solo puede ser captada, según la concepción bergsoniana, mediante la intuición, y nuestra interpretación del tiempo sería t = p1 + p2 + p3 + … pn, es decir, el tiempo sería el conjunto infinito de procesos o cambios que se producen en un Sistema, lo que nos lleva a afirmar que el tiempo histórico es un conjunto de cambios continuos y progresivos producidos en las sociedades hasta nuestros días, en el bien entendido de que esos cambios han de ser “hechos” o “acontecimientos” de relevancia histórica.

–Alberto Vázquez Bragado es Licenciado en Historia por la universidad de Barcelona. Máster en Historia de la Ciencia por la Universidad Autónoma de Barcelona. Formación en Ciencias Económicas, Dirección de Empresas y Literatura. Autor de artículos de investigación en la revista científica Llull y de varios libros de divulgación científica.
Fuente: cinconoticias.com, 22/12/18.

______________________________________________________________________________
Vincúlese a nuestras Redes Sociales: LinkedIn Twitter
______________________________________________________________________________
.
.
Luis Caffarelli, Premio Abel 2023
marzo 22, 2023
El argentino Luis Caffarelli ganó el «Nobel» de Matemáticas: es el primer latinoamericano en lograrlo
A los 74 años obtuvo el Premio Abel, el equivalente al Nobel para las matemáticas. Desde hace décadas reside en Estados Unidos. Cuáles fueron sus mayores contribuciones. Su estudio sobre lo que ocurre en un vaso con hielo.
Por: Gustavo Sarmiento.
Las Matemáticas no tienen Nobel. Lo que usualmente es considerado como «el Nobel» de esa disciplina es el Premio Abel que entrega la Academia de Ciencias y Letras de Noruega en honor al matemático noruego, Niels Henrik Abel, fallecido hace casi un par de siglos. Y la gran novedad, que atañe a nuestro país, es que su edición 2023 la obtuvo el argentino Luis A. Caffarelli, que actualmente vive en Estados Unidos. Es el primer latinoamericano en lograrlo.
Caffarelli ganó el premio por sus «contribuciones fundamentales a la teoría de la regularidad de las ecuaciones diferenciales parciales no lineales, incluidos los problemas de frontera libre y la ecuación de Monge-Ampère», según la información oficial.
Las ecuaciones diferenciales son herramientas que la ciencia utiliza para predecir el comportamiento del mundo físico. Estas ecuaciones relacionan una o más funciones desconocidas y sus derivadas. Las funciones representan generalmente cantidades físicas, las derivadas representan sus tasas de cambio y la ecuación diferencial define la relación entre las dos. Esas relaciones son corrientes, por lo cual, las ecuaciones diferenciales desempeñan un papel de gran importancia en numerosas disciplinas, entre las que se incluyen la física, la economía y la biología.
Las ecuaciones diferenciales parciales aparecen naturalmente como leyes de la naturaleza para describir fenómenos tan diferentes como el fluir del agua o el crecimiento de las poblaciones. Estas ecuaciones fueron objeto constante de intenso estudio desde la época de Isaac Newton y Gottfried Leibniz. Pero las cuestiones fundamentales relativas a la existencia, singularidad, regularidad y estabilidad de las soluciones de algunas de las ecuaciones clave siguen sin resolverse.
Pero pocos matemáticos vivos en todo el mundo contribuyeron tanto a nuestra comprensión de las ecuaciones diferenciales parciales como el argentino nacionalizado estadounidense, quien introdujo nuevas e ingeniosas técnicas, dando pruebas de un brillante conocimiento geométrico y aportando resultados fundamentales.
Un artículo de la embajada de Noruega destaca que un caso emblemático es la teoría de la regularidad: «La regularidad –o suavidad– de las soluciones es esencial en los cálculos numéricos y la ausencia de regularidad mide la salvajez con que naturaleza puede comportarse».
«Los teoremas de Caffarelli han cambiado radicalmente nuestra comprensión de las clases de ecuaciones diferenciales parciales no lineales con amplias aplicaciones. Sus resultados son técnicamente virtuosos y cubren muchas áreas diferentes de las matemáticas y sus aplicaciones», manifestó el presidente del Comité del Premio Abel, Helge Holden.
Lo que ocurre en un vaso con hielo
El trabajo de Caffarelli se refirió durante décadas en gran parte a problemas de frontera libre. Por ejemplo, el problema del hielo que se derrite en el agua: la frontera libre es la interfase o fase intermedia entre el agua y el hielo. Es parte de lo desconocido que está por determinarse. Al derretirse los cubitos, sus aristas se van redondeando. Poco a poco se crea un nuevo mundo en esa frontera entre el sólido y el líquido, con energías y geometrías cambiantes.
“No puedes alcanzar la verdad, pero por lo menos puedes acercarte a ella, a la complejidad de la realidad”, contó el matemático de 74 años. En una nota de El País, contaba: “Las matemáticas vinculadas a la física son las más interesantes. Yo no soy muy partidario de hacer investigaciones superabstractas, que solo puedan entender media docena de matemáticos”.
Otro ejemplo es el agua que se filtra a través de un material poroso, entendiendo la interfase entre el agua y el medio. «Caffarelli aportó soluciones esclarecedoras a estos problemas con aplicaciones a las interfases sólidolíquido, a los flujos de chorro y de cavitación, a los flujos de gases y líquidos en materiales porosos, así como a las matemáticas financieras», acotan desde la Embajada.
Caffarelli también brilló al profundizar en las ecuaciones de Navier-Stokes que describen desde 1845 el flujo de un fluido viscoso, como el aceite. Las aplicaciones son incalculables: desde analizar la circulación sanguínea o predecir el movimiento del petróleo hasta la fabricación del motor de un auto, las matemáticas financieras o el perfeccionamiento de modelos fundamentales que explican el universo.
Claramente no es lo único. Caffarelli publicó más de 320 artículos, realizó más de 130 colaboraciones y asesoró a más de 30 estudiantes de doctorado en un periodo de 50 años. «Al combinar su brillante conocimiento geométrico con ingeniosas herramientas analíticas y métodos, ha tenido y continúa teniendo un impacto muy importante en el campo», afirma Helge Holden. Para tomar dimensión de su importancia en el mundo matemático, los artículos de Caffarelli ya llevan recibidas 19.000 citas por parte de otros científicos y científicas.
Una vida de atracción por la ciencia
Caffarelli nació en Buenos Aires. Cursó en el Colegio Nacional y después estudió Matemáticas en la Universidad de Buenos Aires. En una entrevista años atrás con Juan Luis Vázquez contaba: «Nací y pasé mi juventud en la ciudad de Buenos Aires. Fue una juventud despreocupada durante un periodo relativamente próspero en la Argentina, en un tiempo, la década de los 60, en que había grandes expectativas de cambios y desarrollos científicos a nivel mundial. Siempre me atrajeron la ciencia y la tecnología de manera que tuve que elegir entre ingeniería, matemática o física. Durante aproximadamente un año y medio estudié matemática y física pero finalmente opté por la matemática. Me doctoré en la Universidad de Buenos Aires con una tesis dirigida por Calixto Calderón, y poco tiempo después fui a Minnesota con una beca posdoctoral».
Sus profesores en Argentina lo impulsaron a perfeccionarse en el exterior. Conoció a Gene Fabes y Nestor Riviere en nuestro país, fue a Minnesota (EE UU) por un año, «pero luego distintas circunstancias fueron posponiendo mi regreso».
¿Por qué la Argentina produjo y produce tantos matemáticos brillantes? Esto respondía: «Hans Lewy me contaba que en los EEUU la investigación científica fue un producto de la postguerra. En aquel periodo la Argentina tuvo la fortuna de recibir un flujo importante de científicos europeos de primera línea (Santaló, Balanzat, Beppo Levi, entre los matemáticos) que sentaron las bases de un sistema de educación científica excepcional. Se creó el CONICET, la carrera de investigador, las becas externas, la figura del profesor con dedicación exclusiva, en fin, un sistema que aún seguimos usufructuando entre tantos altibajos económicos».
En la misma entrevista respondía sobre el eterno debate matemática pura versus matemática aplicada o aplicable: «En mi opinión es un debate para puristas. Lo importante es que estamos presenciando uno de los grandes periodos de la matemática. El modelado matemático complejo está ocupando un lugar importante en muchísimas áreas como materiales compuestos, química, biología, finanzas, dinámica de poblaciones, procesamiento de imágenes, estructuras complejas de redes, seguridad de datos. Recordemos además que el modelado envuelve topología, geometría, teoría de números, en fin, todas las áreas. La comunidad matemática tiene dos opciones: aceptar el desafío de participar de esta explosión científica, o aislarse y limitarse».
Y daba su recomendación a los más jóvenes: «Mi recomendación es que la ciencia de hoy es fascinante y está llena de matemáticas. Que no se limite por una habilidad precoz en un rinconcito de las matemáticas, y que se tome el tiempo de descubrir qué es lo que realmente lo apasiona».
Lo que otros no ven
En Minnesota, Caffarelli cambió la dirección de su investigación, después de asistir a una serie de conferencias sobre análisis armónico impartidas por Hans Lewy, matemático estadounidense retirado, nacido en Polonia. Caffarelli le pidió a Lewy indicarle algunos problemas en los que él pudiera trabajar, y Lewy le sugirió “el problema del obstáculo”, un clásico del campo de la regularidad de las ecuaciones elípticas completamente no lineales. La motivación física es determinar la posición que adopta una membrana elástica sobre un obstáculo dado. Caffarelli tuvo que aprender el tema desde cero, y quedó «enganchado». Rápidamente, comenzó a hacer progresos sorprendentes en este tema y en el área más amplia de “problemas de frontera libre”.
Cuenta la Embajada de Noruega que en 1980 Caffarelli se trasladó al Instituto Courant de Ciencias Matemáticas, división independiente de la Universidad de Nueva York. Caminando un día por Chinatown con Robert Kohn y Louis Nirenberg (el ganador del Premio Abel 2015, fallecido en 2020), los tres matemáticos decidieron colaborar en un artículo sobre las ecuaciones de Navier-Stokes, un conjunto de ecuaciones en derivadas parciales no lineales que describen la dinámica de los fluidos: «El resultado de esta colaboración fue Partial regularity of suitable weak solutions of the Navier-Stokes equations, artículo histórico publicado en 1982 que, más tarde, ganaría el Premio Steele 2014 de la American Mathematical Society por su importante contribución a la investigación».
Cuando a Nirenberg le preguntaron más tarde qué pensaba de Caffarelli como matemático, respondió: “Tiene una intuición fantástica, es sencillamente notable … Me costó mucho seguirle el ritmo. De algún modo, ve inmediatamente cosas que los otros no ven”.
Fuente: tiempoar.com.ar, 22/03/23
.
.