Nicolás Steno: Un modelo de investigador

Por María Ángeles Vitoria.

§ 1. NICOLÁS STENO (1638- 1686), CIENTÍFICO INNOVADOR

Se cumplen 350 años de la publicación de dos obras del científico danés Niels Steensen (Nicolás Steno), que constituyen dos piedras miliares de la historia de la ciencia: el Discurso sobre la anatomía del cerebro (O PH II, pp. 1-35), y el De solido intra solidum Naturaliter contento Dissertationis Prodromus (O PH II, pp. 181-226), conocido como Prodromus o De solido. En la primera hace un análisis profundo de la necesidad de una nueva metodología para el estudio de la anatomía del cerebro, pero por sus indicaciones de metodología crítica, tiene un interés que va más allá de la neuroanatomía. Anticipa, además, conceptualmente la técnica de disección de las fibras para estudiar la estructura interna del cerebro. La obra, escrita en un periodo de importantes y encendidos debates sobre las funciones del cerebro, contiene una crítica aguda de algunas tesis defendidas en dos tratados muy influyentes sobre el tema: el de Thomas Willis y el De Homine de Descartes.  Aboga también por un estudio multidisciplinar de la neuroanatomía, que debería abrirse a la embriología, a la anatomía comparada y a la anatomía patológica.

.

El Prodromus se considera la obra que ha dado inicio a la geología como ciencia.

En ella, Steensen demuestra el origen biológico de los fósiles, introduce los conceptos de estrato y de sedimento, enuncia los principios básicos de la geología estratigráfica (de superposición, horizontalidad y continuidad lateral de los estratos), que permiten acceder a la datación relativa de su formación, interpreta correctamente el proceso de crecimiento de los cristales, formula la primera ley de la cristalografía (ley de la constancia del ángulo diedro), si bien  no todavía de modo matemático y universal. Con estos hallazgos puso las bases de tres disciplinas: paleontología, cristalografía y estratigrafía.

La novedad mayor del Prodromus no está en los resultados obtenidos en la investigación, sin duda originales y creativos, sino en el método, en el modo como llega a ellos. Y también, en la introducción de una nueva dimensión en el estudio empírico de la Naturaleza, la dimensión temporal. Se trata de una novedad significativa si se piensa que, hasta la mitad del siglo XVII, la visión dominante de la Naturaleza se basaba en la convicción de una fundamental estabilidad de las estructuras naturales (orgánicas e inorgánicas). Los filósofos naturales estudiaban los objetos de la naturaleza para describirlos y clasificarlos, y los filósofos mecánicos los examinaban para entender cómo funcionaban. Su investigación miraba a describir la Naturaleza tal como es, formulando, en consecuencia, leyes atemporales.

Niels Steensen fue quien incoó científicamente la transición de un mundo estático y mecánico a un mundo más dinámico y en evolución, estableciendo la legitimidad de un estudio empírico de la “historia” de la Tierra. Ciertamente no fue Steensen quien formuló el deep time de la geología. En su época no era posible establecer la edad precisa de la Tierra en términos absolutos. El principio de superposición servía para establecer con seguridad la secuencia, no el número de años transcurridos desde su formación. La geología científica partió con la pregunta, ¿qué ha sucedido primero?, más que con la pregunta, ¿cuánto tiempo hace? (Cutler, 20007). La demostración de Steensen del significado de los fósiles y la metodología que puso en marcha para este estudio, han desempeñado, sin embargo, un papel crucial en el reconocimiento sucesivo de la enorme antigüedad de la Tierra y en la formulación de las teorías evolutivas. Ellenberger considera el Prodromus no sólo «el gran texto fundador de la ciencia geológica», sino «uno de los textos más válidos en la historia de la ciencia», que «todo estudiante y profesor debería meditar expresamente» (Ellenberger,1989). Quizá, estas innovaciones, que abrieron al conocimiento del pasado de las estructuras de la Tierra, pueden paragonarse, de algún modo, a lo que supuso el descubrimiento del electrón en 1897 que introdujo en la exploración del mundo microfisico.

Las obras científico-filosóficas de Steensen, están escritas mayoritariamente en latín (OPH).

Existen buenas traducciones de la totalidad del corpus al inglés (KM) y al italiano (O Sc I, O Sc II). Del Discurso sobre la anatomía del cerebro, redactado originariamente en francés, se encuentran traducciones en varias lenguas: latín, danés, italiano, alemán. El Prodromus es una obra repetidamente traducida en muchas lenguas (francés, danés, japonés, ruso, alemán; además de al inglés y al italiano, como ya he indicado). Leandro Sequeiros publicó en la revista «Enseñanza de la Ciencias de la Tierra» (2002) la traducción completa al castellano de esta obra, lamentando que, hasta ese momento, uno de los libros más importantes de la historia de la Geología, no hubiera sido aún editado en lengua castellana. Posteriormente, junto con Pelayo publicó una obra con la traducción del Prodromus y de otro escrito de Steensen (Canis Carchariae dissectum caput), que viene a ser el precedente del De solido (Sequeiros y Pelayo, 2011).

Con motivo del 350 aniversario de la publicación de estas dos obras pioneras de la historia de las ciencias empíricas, se han promovido diversos encuentros y actividades. Uno de estos tendrá lugar en Roma el 7 de mayo de 2019, en la sede de la Pontificia Universidad de la Santa Cruz, con la participación de profesores e investigadores de diversas universidades de Italia y de Alemania. La información detallada sobre el evento se encuentra en el siguiente link:  https://www.pusc.it/fil/gsteensen19

§2. OTRAS APORTACIONES DEL CIENTÍFICO DANÉS

Como el rey Midas

Niels Stensen afrontó varios campos de estudio. Se ha dicho de él que era como el rey Midas, que cada cosa que tocaba la transformaba en oro, en el oro del conocimiento. Inicialmente se dedicó a la Anatomía, ciencia en la que hizo aportaciones decisivas. Prácticamente no hay parte del cuerpo humano cuyo conocimiento no haya completado y enriquecido con su investigación. En este ámbito son importantes sus trabajos sobre las glándulas, el corazón, el cerebro los músculos y los órganos de la reproducción. Menciono a continuación algunos de estos descubrimientos que manifiestan la gran talla del científico danés.

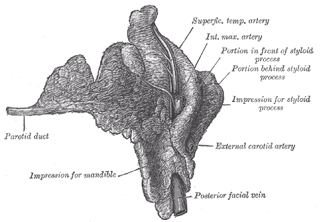
En 1660, al hacer la disección de una cabeza de oveja, descubrió el conducto que lleva la saliva desde la parótida hasta la boca (conducto parotídeo), posteriormente conocido con el nombre de conducto stenoniano. Este hallazgo despertó su interés por el estudio de las glándulas, partes del cuerpo a las que se había prestado poca atención hasta entonces, y que Stensen llega a apreciar como «obras maestras del Creador». Él interpretó correctamente su funcionamiento, mostrando que no son esponjas que absorben las humedades superficiales, y que su actividad no consiste en eliminar excrementos superfluos o nocivos de todo el cuerpo; son órganos que elaboran humores útiles al organismo. Introdujo la distinción entre glándulas de secreción (glándulas propiamente dichas) y linfoglándulas, demostrando, además, que la secreción glandular depende de la aportación de la sangre y de la actividad del sistema nervioso. Corrigió la interpretación de Wharton y de Descartes sobre la formación de las lágrimas. Ellos atribuían su origen a la contracción del cerebro por el dolor. Descubrió también el origen del sudor y de la leche, mostrando la falta de fundamento de las ideas vigentes hasta el momento.

Steensen mostró, además, que el corazón no es la sede del calor vital, como pensaba Galeno y continuaban repitiendo Descartes y otros eruditos; tampoco es la sede del alma. Su estructura es sencillamente la de un músculo. Demostró asimismo que la lengua no es una glándula, como sostenía Wharton, sino que está formada por fibras musculares. Sobre los músculos publicó en 1667 otro tratado –Elementorum Myologiae Specimen seu Muscoli Descriptio Geometrica– que marca un hito en la historia de la fisiología muscular, con la aplicación de las matemáticas a esta parte de la Biología, para mostrar que, durante la contracción, el músculo no cambia significativamente de volumen. Su modelo recibió muchas críticas, pero actualmente ha vuelto a retomarse para la simulación con ordenadores y en las investigaciones sobre los músculos.

Al realizar la disección de un tiburón (los resultados los presenta en la obra Dissectus piscis ex canum genere, identificó por primera vez que los órganos llamados testes muliebres eran, en realidad, los ovarios, donde se producían los óvulos. Posteriormente, por diversas vicisitudes de la historia, se llamaron folículos de Graaf.

Los estudios de Steensen sobre la anatomía del cerebro tienen particular relevancia, tanto desde el punto de vista de la historia de la medicina como desde la perspectiva filosófica. Me he referido ya a su obra más importante sobre el tema, el Discurso sobre la anatomía del cerebro. Este escrito tiene además interés por la confutación que hizo de la tesis cartesiana sobre la glándula pineal, a la cual el filósofo francés, en el De Homine (1662), sobre una base anatómica y fisiológica, le asignaba la función de establecer la interacción entre el cuerpo (res extensa) y el alma (res cogitans). Steensen demostró a través de algunas disecciones realizadas con gran pericia que, por su posición anatómica, la glándula pineal no podía desempeñar las funciones que Descartes le había atribuido, deshaciendo así con una demostración empírica la base científica sobre la que Descartes había desarrollado su teoría. Desde los principios de su sistema, el filósofo francés había afirmado que los animales, siendo sólo res extensa, carecían de alma y, en consecuencia, de glándula pineal; eran, por tanto, simples autómatas. Steensen demostró nuevamente, con el apoyo de disecciones anatómicas cuidadosamente realizadas, la presencia de esta glándula en los animales. Con cierta dosis de humor comentaba que le gustaría tener la certeza que decían poseer los cartesianos acerca de la ausencia de sensibilidad en los animales (por no tener alma), que los llevaba a sostener que no existía diferencia entre seccionar o quemar un nervio o las cuerdas de un autómata. Si yo -decía Steensen- tuviese esa certeza, no experimentaría malestar al practicar la vivisección, y podría continuar trabajando sin preocupación con animales el tiempo que fuese necesario.

§3. BREVE PERFIL BIOGRÁFICO, CIENTÍFICO Y ESPIRITUAL DE NIELS STEENSEN

Niels Steensen (1638-1686) nació en Copenhague, en el seno de una familia de pastores luteranos. Después de haber estudiado medicina en su ciudad natal, se trasladó a Holanda en 1660 para continuar los estudios de anatomía. La afabilidad de su carácter y su categoría intelectual, le facilitaron la amistad con personalidades científicas de la época (Swammerdam y Spinoza, entre otras). En Holanda hizo los descubrimientos anatómicos sobre las glándulas y el corazón a los que me he referido en el apartado anterior.

Académie Royal des Sciences

En 1665 viajó a París, donde fue introducido en el círculo del diplomático y protector de las ciencias Melchisédech Thévenot, frecuentado por jóvenes naturalistas, matemáticos y humanistas, como Christian Huygens, Blaise Pascal, Jan Swammerdam, Pierre Borel. De este grupo de intelectuales e investigadores nació en 1666 la Académie Royal des Sciences. En una de las reuniones promovidas por Thévenot, Steensen pronunció el famoso Discurso sobre la anatomía del cerebro.

En el mes de febrero de 1666, Steensen llegó a Italia, donde fue acogido por el Gran duque de Toscana, Fernando II, y por su hermano, el príncipe Leopoldo, promotor de la Academia del Cimento, una institución fundada en 1657 que estaba constituida por científicos que deseaban continuar la perspectiva experimental y matemática de Galileo. Los años 1666 al 1669, transcurridos fundamentalmente en Toscana, fueron muy fecundos para Steensen. En efecto, en este periodo escribió un tratado sobre los músculos en clave geométrica, formuló algunos de los conceptos y principios fundamentales de la geología (contenidos principalmente en el Prodromo y se convirtió al catolicismo (2 de noviembre de 1667).

Ordenado sacerdote en la catedral de Santa Maria del Fiore (Florencia)

Después de la conversión continuó con la investigación en anatomía y geología. Viajó por algunos países de Europa, fundamentalmente para estudiar las formaciones geológicas, y continuó practicando la anatomía. Publicó varias obras. Una de las más conocidas es la prolusión que pronunció en la Domus Anatomica de Copenhague el 29 de enero de 1673 (OPH II, pp. 249-256), antes de proceder con la disección del cadáver de una mujer. En abril de 1675 fue ordenado sacerdote en la catedral de Santa Maria del Fiore (Florencia), y en septiembre de 1677 fue consagrado obispo en el palacio de Propaganda Fide (Roma). Desde el momento de su ordenación sacerdotal, se dedicó totalmente a la tarea pastoral, con la misma pasión que caracterizó su trabajo como investigador. Fue nombrado Vicario Apostólico de Hannover, ciudad en la que tuvo diversos encuentros con Leibniz sobre cuestiones científicas, filosóficas y teológicas. Posteriormente fue nombrado Vicario Apostólico de Münster y enviado a Schwerin, donde murió el 25 de noviembre de 1686. Sus restos mortales descansan en la insigne basílica de San Lorenzo de Florencia.

Beatificación de Steensen

Tres siglos más tarde, el 23 de octubre de 1988, Niels Steensen fue beatificado por Juan Pablo II, siendo el primer científico moderno que ha recibido el honor de la beatificación. Su fiesta se celebra el 5 de diciembre.

En la homilía pronunciada durante la misa de beatificación del científico danés (23 noviembre 1988), Juan Pablo II puso de relieve la admirable unidad de pensamiento y de vida con la que Steensen supo mirar la Naturaleza. «Toda la vida de Steensen ha sido un incansable peregrinar en la investigación de la verdad, de la verdad científica y de la verdad religiosa, con la convicción de que todo descubrimiento, aunque sea modesto, constituye un paso adelante hacia la Verdad Absoluta, hacia aquel Dios del que depende todo el universo». (Para acceder al texto completo en italiano, pínchese aquí) 

El método de Steensen

Los hallazgos de Steensen fueron fruto de las elecciones metodológicas que realizó y de cualidades personales muy destacadas. En cuanto al método, podemos decir a grandes rasgos, que su exploración fue una investigación genuinamente empírica, sostenida por el primado de la observación directa y personal de la Naturaleza, en sinergia con el esfuerzo por librarse de prejuicios o ideas preconcebidas, no plenamente ancladas en la experiencia. Una actitud, por tanto, de clara matriz baconiana.

Steenssen supo mantener un equilibrio saludable entre primado de la observación personal y respeto a las autoridades en materia científica. Él consideró la experiencia como juez inapelable que decide sobre la validez de una hipótesis, pero tuvo en cuenta también las teorías acreditadas hasta ese momento, mientras no existiesen indicaciones empíricas de signo contrario. Refiriéndose a quienes no prestaron atención a los que afirmaban que el corazón era un músculo, dice: «Si estos hombres ilustres, en lugar de estar más interesados en repetir su discurso, hubiesen buscado la verdad, y si en lugar de preferir las cosas que ellos habían imaginado, hubiesen prestado atención a los principios que se obtienen de la observación de los fenómenos naturales, no habrían formulado juicios precipitados sobre ésta y otras cuestiones» (O PH I, p. 163). Steensen admiró la filosofía cartesiana pero al advertir que la pretensión de reconducir todas las certezas a la sola evidencia intelectual estaba al servicio de la absoluta autonomía de la razón, perdió confianza en este sistema racionalista. Según el científico danés, Descartes había puesto demasiada confianza en el razonamiento puramente deductivo, y muy poca en las observaciones empíricas. Steensen, en cambio, aplicó la regla cartesiana con un concepto más amplio de evidencia. «Yo trato de seguir las leyes de la filosofía que nos enseñan a buscar la verdad dudando de su certeza y a no quedar satisfechos antes de estar convencidos de la evidencia de la demostración» (O PH II, p.23). Por eso, escribió: «A Descartes no le reprocho el método, sino el abandono del método» (O TH I, p. 390).

Junto con el método influyeron positivamente en su investigación algunas de las cualidades que poseía. Eran extraordinarias su habilidad y capacidad de observación, su facilidad para evitar los detalles circunstanciales y quedarse sólo con lo que era esencial al problema estudiado. Era proverbial su rigor en la aplicación de los protocolos. Repetía los experimentos hasta tener seguridad de los resultados y procuraba realizarlos a la vista de otros científicos, para que pudiesen confirmarlos. Fue extraordinariamente prudente en el pronunciarse sobre las conclusiones. Prefería no cantar eureka antes de haber obtenido la victoria. Tampoco se detenía ante los problemas que levantaban nuevas observaciones o conocimientos, sino que afrontaba una a una las dificultades, tomando en consideración todos los razonamientos en favor y en contra de la hipótesis que él sostenía.

Una fuerte personalidad unitaria

Los estudiosos del perfil espiritual de Steensen coinciden en el subrayar la fuerte personalidad unitaria del científico danés. Ciencia y fe-teología fueron para él dos niveles epistémicos diferentes, que requerían métodos diversos. Pero más allá del plano metodológico abstracto, se unían estrechamente en el nivel de la inteligencia vital. Él realizó una investigación genuinamente empírica, sin introducir referencias teológicas en sus argumentaciones. A la vez, una motivación de fondo religioso -descubrir la grandeza del Creador, hacerlo amar- le generó una actitud afectiva que redundó muy positivamente en su trabajo, moviéndole a trabajar con entusiasmo y a proseguir cuando surgían dificultades. Steensen reconoció que la mirada teística potenció y sostuvo su natural capacidad de observación y de reflexión, orientándole hacia el estudio de algunas partes del cuerpo que, de otro modo, hubiese descuidado.

§4. INDICACIONES BIBLIOGRÁFICAS 

Obras de Niels Steensen

Las obras de Niels Steensen están recogidas en seis volúmenes: dos contienen las aportaciones de carácter científico-filosófico, dos las de tema teológico, y las otras dos, recogen las cartas escritas por Steensen y las dirigidas a él:

Maar, V.E. (ed.) (1910). Nicolai Stenonis opera philosophica, 2 vol. Copenhagen: Vilhelm Tryde.

Larsen, K. y Scherz, G. (eds) (1944 – 1947). Nicolai Stenonis opera theologica cum prooemiis ac notis Germanice scriptis, 2 vol. Hafniae – Freiburg: Nyt Nordisk Forlag.

Scherz, G. (ed) (1952).  Nicolai Stenonis epistolae et epistolae ad eum datae cum proemio ac notis Germanice scriptis, 2 voll. Hafniae, Herder – Freiburg: Nyt Nordisk Forlag. Las abreviaturas usuales para citar estas obras son, respectivamente: OPH, OTH, EP.

Las obras científico-filosóficas están traducidas al italiano en su totalidad: Casella, L. y Cotturi, E. (eds) (1986). Niccolò Stenone. Opere scientifiche, 2 vol, (eds). Firenze: Nuova Europa Editrice. Las abreviaturas usuales son:  O Sc I, O Sc II.

Existe también traducción al inglés de toda la obra científico-filosófica de Steensen: Kardel, T. y Maquet, P. (eds) (2013). Nicolaus Steno: Biography and Original Papers of a 17th Century Scientist. Berlin: Springer. Esta edición incluye la traducción al inglés de la primera parte de la biografía de Steensen escrita por Scherz.  Usualmente se abrevia con la sigla KM.

Página web oficial sobre el científico danés: https://nielssteensen.dk/ 

Algunas biografías del científico danés y escritos sobre su perfil espiritual y científico

Scherz, G. (1987-1988). Niels Stensen: Eine Biographie, 2 vol, Leipzig: St Benno Verlag.

Angeli, R. (1996). Niels Stensen. Filosofo della scienza, testimone della fede, «beato» per la Chiesa.  Cinisello Balsamo: San Paolo.

Para una visión de conjunto de la vida y del significado del trabajo de Niels Steensen, es útil la lectura de la voz “Niels Steensen” escrita por F. Abbona en el Dizionario Interdisciplinare di Scienza e Fede, vol 2, G. Tanzella-Nitti, A. Strumia (eds) (2002). Roma – Città del Vaticano: Urbaniana University Press – Città Nuova Editrice, pp. 2099-211

Otras obras y artículos de interés:

Andrault, R. y Lærke, M. (eds) (2018). Steno and the Philosophers. Kominklijke Leiden: Brill’s Studies in Intellectual History 276.

Miniati, St. (2009). Nicholas Steno’s Challenge for Truth. Reconciling Science and Faith. Milano: Franco Angeli (sexta reimpresión 2015)

Sobiech, F. (2004). Herz, Gott, Kreuz. Die Spiritualität des Anatomen, Geologen und Bischofs Dr. Med. Niels Stensen (1638-1686). Münster: Aschendorff Verlag.

Sobiech, F. (2015). Puntero en la mano de Dios. Ética y Bioética en la obra y en la recepción del anatomista Niels Stensen (1638-1686). Chile: Nueva Patris.

Vai, G.B. (2009). “The Scientific Revolution and Nicholas Steno’s Twofold conversion”, en Rosenberg, G.D. (ed), The Revolution in Geology from the Renaissance to the Enlightenment. Geological Society of America Memoir 203, 187-208.

Vinaty, B. (1991). “Il profilo spirituale di Niels Steensen”, Quaderni di Niccolò Stenone,1, 73-96.

Textos sobre el significado del trabajo de Steensen en Geología

(Se indican también tratados generales que contiene juicios amplios sobre Steensen).

Cutler, A. (2003). The Seashell on the Mountaintop. New York: Dutton. Traducción al castellano (2007). Una nueva historia de la Tierra. Un relato sobre la ciencia y Nicolaus Steno, el genio que descubrió la geología. Barcelona: RBA Libros. Traducción al italiano (2007). La conchiglia del diluvio. Niccolò Stenone e la nascita della scienza della Terra. Milano: Il Saggiatore.

Ellenberger, F. (1989). Historia de la Geología (vol 1): de la Antigüedad al siglo XVII. Barcelona: Labor.

Gohau, G. (1987). Histoire de la géologie. Paris: La Découverte.

Gohau, G. (1990). Les sciences de la Terre aux XVII e XVIII siècles. Naissance de la géologie. Paris: Albin Michele.

Morello, N. (1979). La nascita della Paleontologia nel Seicento: Colonna, Stenone e Scilla. Milano: Franco Angeli.  

Rudwick, J.S. (1987). El significado de los fósiles. Episodios de la historia de la Paleontología. Madrid: Hermann Blume.

Sequeiros, L. y Pelayo, F. (2011). Nicolás Steno, los estratos y el Diluvio. Un encuentro entre ciencia y religión en el siglo XVII. Madrid: Universidad Pontificia Comillas (contiene la traducción del Canis Carchariae dissectum caput y del Prodromo al castellano)

Textos sobre su aportación a la neuroanatomía

Andrault, R. (2018). Human Brain and Human Mind: The Discourse on the Anatomyof the Brain and Its Philosophical Reception, en Andrault, R y Laerke, M. (eds) Steno and the Philosophers. Leiden – Boston: Brill.

Clarke,E.S. (1968). Brain anatomy before Steno en Scherz, G., Steno and brain research in the seventeen century. Oxford: Pergamon Press.

Djørup, F. (1968). Las ideas de Steno sobre la investigación del cerebro en Scherz, G., Steno y la investigación del cerebro en el siglo diecisiete . Oxford: Pergamon Press.

Faller, A. (1978). Nicolaus Stenonis. Anatomista, geólogo y obispo. La aventura de una vida ricamente conmovedora . Friburgo: Discursos de la Universidad de Friburgo.

---

─María Ángeles Vitoria. Estudió Biología y Filosofía. Actualmente es profesor Asociado de Filosofía de la naturaleza y de la ciencia en la Pontificia Universidad de la Santa Cruz. Ha trabajado los aspectos epistemológicos e histórico-humanísticos de la actividad científica, y sus relaciones con la fe.

Fuente: https://proyectoscio.ucv.es/articulos-filosoficos/nicolas-steno/

---

.

.

Desnudando el posmodernismo y la pseudociencia

Por Albert Mesa Rey.

En la década de 1990, el físico Alan Sokal y el matemático Jean Bricmont sacudieron los cimientos de la academia con su libro «Imposturas Intelectuales«. Este controvertido trabajo, también conocido como «Fashionable Nonsense» en inglés, se sumerge en el mundo de la posmodernidad y la pseudociencia, revelando cómo algunas teorías y discursos académicos en disciplinas como la sociología, la filosofía y los estudios culturales han caído presa de la jerga vacía y la falta de rigor intelectual.

El engaño de Sokal:

El engaño de Sokal se centra en el artículo titulado «Transgressing the Boundaries: Toward a Transformative Hermeneutics of Quantum Gravity» (Transgrediendo los límites: hacia una hermenéutica transformadora de la gravedad cuántica), publicado en 1996 en la revista cultural «Social Text«. Este artículo, escrito por el físico teórico Alan Sokal, fue diseñado como una amalgama de jerga científica sin sentido y conceptos aparentemente profundos que, en realidad, carecían de cualquier validez científica.

El objetivo de Sokal era poner a prueba la disposición de ciertos académicos en las disciplinas de humanidades para aceptar afirmaciones pseudocientíficas si estas coincidían con sus preconcepciones ideológicas o filosóficas. En otras palabras, quería demostrar que algunos círculos académicos estaban dispuestos a pasar por alto la falta de rigor científico con tal de respaldar teorías que se alinearan con sus creencias.

El artículo de Sokal utilizó términos científicos complejos y referencias aparentemente eruditas, pero al analizarlo más detenidamente, resultaba claro que las ideas presentadas eran inconsistentes, incoherentes y, en última instancia, desprovistas de cualquier fundamento científico real. Sokal mismo reveló el engaño al hacer público que el artículo era una parodia destinada a destacar la falta de rigor y el abuso del lenguaje científico en algunas corrientes intelectuales.

Este acto de Sokal generó un debate considerable en el mundo académico sobre la integridad intelectual y la necesidad de mantener altos estándares en la investigación y el discurso académico. Mientras algunos apoyaron su acción como un intento necesario de señalar las debilidades en ciertos campos, otros lo criticaron por considerarlo deshonesto y argumentaron que Sokal no entendía completamente las complejidades de las disciplinas que estaba criticando.

En última instancia, el engaño de Sokal tuvo un impacto duradero al resaltar la importancia de mantener una base sólida en la investigación y la comunicación académica, así como al cuestionar la apropiación superficial de la jerga científica en contextos que no son científicos.

La crítica de Sokal y Bricmont:

«Imposturas Intelectuales» no se limita a exponer el engaño de Sokal, sino que profundiza en la crítica a una serie de pensadores posmodernos, entre ellos Jacques Lacan, Julia Kristeva y Jacques Derrida. Sokal y Bricmont argumentan que estos autores han abusado de conceptos científicos para respaldar teorías que, en última instancia, carecen de rigor y fundamentos sólidos. A continuación, se destacan los puntos clave de su crítica:

1. Uso inapropiado de la jerga científica: Sokal y Bricmont argumentan que muchos autores posmodernos utilizan un lenguaje científico sofisticado de manera incorrecta o sin comprender completamente los conceptos que están empleando. Esto, según ellos, crea una ilusión de profundidad y rigor intelectual sin realmente fundamentar sus afirmaciones en la metodología científica adecuada.
2. Confusión entre ciencia y especulación teórica: Los críticos sostienen que hay una tendencia a mezclar la terminología científica con especulaciones teóricas, creando una confusión entre lo que es un hecho respaldado por la evidencia y lo que es una interpretación o teorización más libre. Esto, según Sokal y Bricmont, diluye la distinción entre la ciencia y otras formas de conocimiento.
3. Falta de rigor y claridad conceptual: Los autores sostienen que algunos pensadores posmodernos carecen de rigor en sus argumentos y teorías, lo que conduce a la proliferación de ideas sin una base sólida. Argumentan que este tipo de laxitud intelectual debilita la integridad académica y socava la capacidad de las disciplinas para contribuir al conocimiento humano.
4. Relativismo y negación de la verdad objetiva: Sokal y Bricmont critican la tendencia posmoderna hacia el relativismo cultural y la negación de la existencia de verdades objetivas. Argumentan que esto debilita la búsqueda de la verdad y socava la capacidad de llegar a consensos basados en la evidencia y el razonamiento lógico.
5. Falta de responsabilidad intelectual: En última instancia, los críticos abogan por una mayor responsabilidad intelectual y un retorno a estándares más rigurosos en la academia. Argumentan que la falta de claridad conceptual y la apropiación indebida de la jerga científica debilitan la credibilidad de las disciplinas académicas y obstaculizan el avance del conocimiento.

La crítica de Sokal y Bricmont ha generado debates profundos sobre la relación entre la ciencia, la filosofía y las humanidades, así como sobre la necesidad de mantener altos estándares intelectuales en el ámbito académico.

Reacciones y controversias:

Las reacciones y controversias tras el engaño de Sokal fueron extensas y abarcaron una variedad de perspectivas dentro del mundo académico y más allá. A continuación, se destacan algunas de las principales respuestas y debates generados por la acción de Sokal:

1. Apoyo a Sokal:
   • Defensa de la Integridad Académica: Muchos académicos y científicos apoyaron la iniciativa de Sokal, considerándola una llamada de atención necesaria sobre la falta de rigor en ciertos campos académicos y la importancia de mantener estándares elevados en la investigación.
2. Críticas a Sokal:
   • Falta de Comprensión Disciplinaria: Algunos críticos argumentaron que Sokal no entendía completamente las complejidades y metodologías específicas de las disciplinas que estaba criticando. Sostuvieron que su acción era una simplificación excesiva y despectiva de las contribuciones intelectuales de esas áreas.
3. Debates sobre Ética y Honestidad:
   • Deshonestidad vs. Revelación de Problemas Sistémicos: Surgió un debate sobre si la acción de Sokal era ética. Algunos creían que su engaño era deshonesto y socavaba la confianza en la investigación académica, mientras que otros argumentaban que revelaba problemas sistémicos en ciertas corrientes intelectuales.
4. Reflexión sobre Posmodernismo:
   • Cuestionamiento del Posmodernismo: El engaño de Sokal provocó un cuestionamiento más profundo sobre las bases del posmodernismo y sus implicaciones para la investigación académica. Algunos sugirieron que el posmodernismo, al enfatizar la relatividad de la verdad, había llevado a una falta de escrutinio crítico en la evaluación de las ideas.
5. Impacto en el Debate Académico:
   • Fomento del Debate sobre Rigor y Claridad: A pesar de las críticas, el engaño de Sokal sirvió como catalizador para un debate más amplio sobre la importancia del rigor y la claridad conceptual en la investigación académica. La comunidad académica se vio impulsada a reflexionar sobre la necesidad de salvaguardar la integridad intelectual.
6. Continuación del Diálogo:
   • Conversaciones sobre la Ciencia y las Humanidades: El incidente impulsó conversaciones más amplias sobre la relación entre la ciencia y las humanidades, así como sobre cómo estas disciplinas podrían beneficiarse de un diálogo más efectivo y respetuoso.

En conjunto, el engaño de Sokal desencadenó un diálogo profundo sobre la naturaleza de la investigación académica, los límites éticos de la crítica y la importancia de mantener altos estándares intelectuales en todas las disciplinas. Aunque las opiniones varían, su acción sigue siendo un evento significativo en la historia del pensamiento académico contemporáneo.

Conclusiones:

El engaño de Sokal provocó una serie de conclusiones y reflexiones en el ámbito académico y más allá. Algunas de las conclusiones clave derivadas de este incidente incluyen:

1. Necesidad de Rigor Académico:
   • La acción de Sokal destacó la importancia de mantener altos estándares de rigor en la investigación académica. La falta de fundamentos científicos en su artículo paródico puso de manifiesto la necesidad de una revisión crítica constante y una aplicación rigurosa de los principios metodológicos.
2. Diálogo Interdisciplinario:
   • El incidente generó debates sobre la necesidad de un diálogo más efectivo entre las disciplinas científicas y humanísticas. Destacó la importancia de comprender y respetar los métodos y enfoques particulares de cada campo para fomentar una colaboración más fructífera.
3. Ética en la Investigación:
   • Se intensificó el debate sobre la ética en la investigación académica. La pregunta sobre si el engaño de Sokal era ético o si era necesario para resaltar problemas sistémicos llevó a una mayor reflexión sobre los límites de la crítica y la responsabilidad del investigador.
4. Desafío al Posmodernismo:
   • El engaño desafió las bases del posmodernismo al poner de manifiesto la falta de escrutinio crítico en ciertas corrientes intelectuales. Surgieron preguntas sobre la validez de las ideas posmodernas y su impacto en la forma en que se aborda la verdad y el conocimiento.
5. Reflexión sobre la Comunicación Científica:
   • El incidente llevó a una reflexión más profunda sobre la comunicación científica y la importancia de transmitir de manera clara y precisa los conceptos científicos. Destacó la necesidad de evitar la apropiación superficial de la jerga científica en contextos no científicos.
6. Concienciación sobre Problemas Sistémicos:
   • La acción de Sokal sirvió como una llamada de atención sobre problemas sistémicos en la academia, incluida la falta de escrutinio en la revisión por pares y la posibilidad de aceptar afirmaciones sin fundamentos sólidos si coincidían con ciertas ideologías.

En resumen, el engaño de Sokal dejó una huella significativa en el mundo académico, provocando debates fundamentales sobre la ética en la investigación, la comunicación entre disciplinas y la necesidad de mantener estándares elevados en la búsqueda del conocimiento. Su acción sigue siendo recordada como un hito en la historia de la crítica académica y la defensa de la integridad intelectual.

Fuente: adelanteespana.com, 20/01/24

---

.

.

La utilidad de la Historia

¿La Historia es una ciencia?

Por Alberto Vázquez Bragado.

Se sabe que, en Historia, es prácticamente imposible obtener teorías o leyes generales de forma deductiva y más tarde soportar un experimento como sucede en las ciencias sociales, pues lo histórico viene ya de experiencias vividas, de observaciones a lo largo del tiempo. ¿Qué experimentación habrían de precisar?

Desde luego que ninguna. La Historia, como tal, es una ciencia social en la que intervienen infinidad de variables y donde las constantes pueden cambiar con facilidad; por lo tanto, bajo esa perspectiva, es difícil elaborar leyes generales tal como lo entiende la comunidad científica y muchos pensadores.

Las proporciones científicas

Pero, ¿qué entendemos por teorías o leyes generales? Podría valernos el considerarlas como un conjunto de supuestos a partir de los cuales, mediante razonamientos lógicos, sería posible deducir hechos, sucesos o acontecimientos del tipo de:

“identificada científicamente una cosa, situación o proporción, mediante cálculos aritméticos o razonamientos lógicos, deducimos o predecimos otra, o sea: (A) mediante (r), se convierte en (B)”.

Por ejemplo, en la ciencia natural por antonomasia, que es la física newtoniana, el espacio recorrido por un cuerpo es igual a la velocidad que lleva ese cuerpo, multiplicado por el tiempo que tarda en recorrerlo (E = V x T); o, en la ley de la palanca, donde Potencia por su brazo es igual a la Resistencia por el suyo (P x b1 = R x b2).

Todo ello ¿Qué nos está diciendo? Bajo mi punto de vista lo que nos están diciendo todas estas fórmulas o ecuaciones es que existen unas proporciones, unas equivalencias entre las partes y el todo; por ejemplo, entre velocidad y tiempo con el espacio, y también entre las partes, o sea, entre velocidad y tiempo entre sí.

En el segundo ejemplo, se podría decir que existe una proporción o correspondencia máxima -que llega a la igualdad- entre dos elementos, aparentemente distintos, que son los dos miembros de la ecuación, (P x b1) por un lado y (R x b2) por el otro; de tal forma que si al primer miembro lo llamamos (A) y al segundo miembro lo llamamos (B), A : B =  1, o lo que es lo mismo, la proporcionalidad mínima o máxima, según se mire, es la igualdad, y a partir de ese punto diremos que un elemento es poco o muy proporcional a otro.

Puede ser directamente proporcional, en razón de sus magnitudes, de forma que cualquier cambio del primer elemento produce un cambio cuantitativo o cualitativo del segundo en el mismo sentido; e inversamente proporcional, de forma que cualquier cambio del primer elemento origina un cambio del segundo, pero en sentido inverso.

Las proporciones de los hechos históricos

El análisis anterior nos sirve para despejar dudas y tener un punto de partida no “contaminado” de la gran cantidad de fórmulas, modelos y opiniones que existen sobre el particular, y que nos llevan a afirmar que, en cualquier teoría o ley general, existen proporcionalidades entre los diferentes elementos, sucesos, hechos, fenómenos…

Y en la Historia y las ciencias sociales se pueden encontrar proporcionalidades, relaciones y análisis entre muchos de sus elementos, sucesos, hechos y fenómenos, como sucede en las ciencias naturales. La cuestión es que las matemáticas y la física necesitan proporciones máximas y no se conforman con proporciones menores, es decir, las matemáticas y la física no pueden permitirse el más mínimo error en la mayoría de los casos, y por ello buscan teorías que se puedan plasmar en igualdades y ecuaciones, pero las ciencias sociales, y en especial la Historia, no precisan tanto, se conforman con encontrar regularidades y analogías.

Carl G. Hempel afirma en su obra La explicación científica, que sería más correcto hablar de “hipótesis universales” en lugar de hacerlo de “leyes generales”, y que buscar una “hipótesis universal” en la Historia debería hacerse bajo el presupuesto de hallar una hipótesis que afirme una regularidad del siguiente tipo:

“en todos los casos en donde un hecho de una clase específica C ocurre en un cierto lugar y tiempo, otro hecho de una clase específica E ocurrirá en un lugar y tiempo relacionados de un modo específico con el lugar y el tiempo de ocurrencia del primer suceso.”

Simetrías y semejanzas

El modelo de hipótesis de Hempel hace que me sienta cómodo, sobre todo, porque es el modelo más común que aparecerá casi siempre en cualquier hipótesis histórica que se quiera formular, al incorporar dos factores fundamentales de la historia: espacio y tiempo, sin los cuales la historia no tendría sentido.

Sin embargo, lo que la Historia no puede establecer es “en todos los casos”, y, en ese sentido, la Historia no puede ni debe pretender ser una ciencia que pueda crear modelos matemáticos de ecuaciones e igualdades, ni tampoco establecer una “ley general” que pueda ser refutada por motivo de una sola predicción que no se cumpla, como afirman los racionalistas con Karl Popper a la cabeza.

Mi opinión es que, a la Historia le basta con establecer proporcionalidades y analogías entre hechos, elementos, sucesos o acontecimientos del pasado con respecto al presente, y que, gracias al modelo inductivo –el mejor por ser histórico–, se puedan predecir tendencias futuras e incluso, utilizando la estadística, analogías y semejanzas.

Resumiendo, las ciencias exactas precisarán ecuaciones algebraicas para establecer la “ley general”, y las ciencias naturales precisarán experimentaciones científicas rigurosas o demostraciones algebraicas para ser aceptadas; en cambio, las ciencias sociales se conforman con “esbozos de ley general” o proporcionalidades.

En palabras más sencillas, las ciencias exactas se identifican con igualdades; las ciencias naturales se identifican con igualdades fiables, es decir, sometidas a refutación experimental; y las ciencias sociales establecen proporcionalidades y analogías a través de series de hechos similares comprobados, que darían origen a un sistema de probabilidades que pudiera establecer una “ley general”.

En ese sentido, la Historia sería la ciencia más adecuada y fiable para poder establecer hipótesis del tipo inductivo, ya que los (n) elementos, hechos, sucesos o acontecimientos que puede presentar como prototipos, son de una gran seguridad y solvencia al tratarse de elementos, hechos, sucesos o acontecimientos históricos, teniendo, además, como elemento catalizador al tiempo, que es consustancial con la Historia y fundamental a la hora de valorar si un determinado suceso está sometido o no a una ley general; es decir, se puede someter a una ley general válida, y se puede estudiar y analizar bajo el punto de vista de las ciencias naturales o, por el contrario, es un suceso singular que se deberá estudiar y analizar bajo el prisma de las ciencias humanas o del espíritu; o sea, nosotros opinamos con convicción que muchos sucesos históricos podrían estar sometidos a leyes generales para pequeños periodos de tiempo, y, por otro lado, también estamos convencidos de que muchas leyes generales establecidas desde las ciencias naturales en un tiempo ilimitado, podrían no tener validez.

Leyes naturales y leyes sociológicas

Consideremos un ejemplo. Históricamente, está constatado que, en una amplia sociedad, cuanto más se incrementa la clase media menos posibilidades hay de que haya grandes revoluciones. Llamando a la sociedad A y a la clase media B, se producirá que, a medida que la clase media aumenta, el riesgo de revolución R disminuye convirtiéndose en R’, siendo B y R cuantificable en número, cantidad o dimensión. Contrariamente, a medida que la clase media disminuye, el riesgo de revolución aumenta; por lo tanto, creemos que existe una proporcionalidad que se puede constatar históricamente, pero que no podemos asegurar que se cumplirá siempre y en cualquier lugar.

Sin embargo, sí se producirá una cuasi igualdad en forma de ecuación que diga: en una sociedad de ciertas dimensiones A, y en tiempo (t) suficientemente pequeño:  B’ / B = R / R’, de tal forma que, cuando en la sociedad A, con una clase media B, y en un tiempo muy corto, a medida que aumenta la clase media disminuirán las revoluciones, ya sea en cantidad o intensidad.

Cierto es que no podemos estar seguros de que esa igualdad se seguirá produciendo en el futuro, puesto que la ecuación nace de una inducción histórica y, bajo el punto de vista de las ciencias naturales, nadie puede asegurar que esa ley se siga produciendo en un tiempo futuro ilimitado, pero existen una serie de elementos psicológicos y sociológicos de la sociedad que aseveran que es más fácil que una sociedad se revele violentamente contra el orden establecido y las instituciones cuando esa sociedad está formada por una mayoría de clase baja, que si está formada por una mayoría de clase media.

Resumiendo, podemos afirmar que, en un tiempo corto, muchas leyes inductivas serían tan válidas como las leyes deductivas y, por consiguiente, podemos afirmar que, en el corto plazo, existen muchas generalidades de carácter histórico que se podrían emplear discretamente para conocer mejor el pasado, y prevenir cuidadosamente el futuro, o lo que es lo mismo: las aproximaciones y tendencias, en el corto plazo, pueden tener validez para la historia.

El continuo e infinito tiempo

Nuestro punto de vista sobre el tiempo es el siguiente:

El tiempo podría ser relativo para cada Sistema, partiendo de una unidad global que es el mundo, como el conjunto de galaxias; nuestro mundo correspondería a la constelación de la Vía Láctea y la Tierra, donde vive la humanidad, gira alrededor de una estrella incandescente llamada Sol, que es de donde recibe el calor para producir y mantener a los seres vivientes del planeta Tierra, y, por ende, la vida del ser humano.

Pues bien, dejando de lado el tiempo de esa unidad global del Mundo, nuestro tiempo será la magnitud que mide los procesos de rotación y traslación de la Tierra alrededor del Sol, pero si hacemos un esfuerzo de abstracción mental o, como dirían Horkheimer y Adorno, “logramos separar el sujeto del objeto mediante un esfuerzo mental” al mismo tiempo que nos olvidamos del día, de la noche, de los relojes…, ¿qué sería el tiempo para nosotros?  ¿No sería algo vacío, solo medible por el envejecimiento de nuestro cuerpo, el crecimiento de plantas, el nacimiento de criaturas, su crecimiento o el deterioro de las cosas que nos rodean?

Por lo tanto, nosotros creemos que el tiempo siempre está ligado a “acción” y movimiento, y lo que el ser humano identifica como tiempo en realidad es duración, cosa que ya Bergson lo afirmaba en su obra La Evolución Creadora, donde asevera que nuestra inteligencia tiende a considerar el tiempo de una forma rectilínea y distingue de modo artificial el pasado, presente y futuro, mientras que, para la auténtica realidad de la conciencia, el tiempo es duración (durée), o sea, algo no susceptible de reducirse a un instante, porque es un flujo continuo “cuyos momentos sucesivos no pueden separarse”. Por consiguiente, la duración solo puede ser captada, según la concepción bergsoniana, mediante la intuición, y nuestra interpretación del tiempo sería t = p1 + p2 + p3 + … pn, es decir, el tiempo sería el conjunto infinito de procesos o cambios que se producen en un Sistema, lo que nos lleva a afirmar que el tiempo histórico es un conjunto de cambios continuos y progresivos producidos en las sociedades hasta nuestros días, en el bien entendido de que esos cambios han de ser “hechos” o “acontecimientos” de relevancia histórica.

–Alberto Vázquez Bragado es Licenciado en Historia por la universidad de Barcelona. Máster en Historia de la Ciencia por la Universidad Autónoma de Barcelona. Formación en Ciencias Económicas, Dirección de Empresas y Literatura. Autor de artículos de investigación en la revista científica Llull y de varios libros de divulgación científica.

Fuente: cinconoticias.com, 22/12/18.

______________________________________________________________________________

Vincúlese a nuestras Redes Sociales: LinkedIn      Twitter

______________________________________________________________________________

.

.

Matemáticas: ¿descubrimiento o creación?

Las matemáticas… ¿nos las inventamos o las descubrimos? Un milenario debate sin resolver

Por Hannah Fry, matemática. 28 octubre 2018

Hay un misterio en el corazón de nuestro Universo. Un rompecabezas que, hasta ahora, nadie ha podido resolver. De resolverlo, las consecuencias serían profundas.

El misterio es por qué las reglas y los patrones matemáticos parecen infiltrarse en casi todo el mundo que nos rodea. De hecho, hay quienes describen las matemáticas como el lenguaje subyacente del Universo.

¿Significa eso que es algo que simplemente hemos ido descubriendo? ¿O es algo que hemos ido inventando, como cualquier lenguaje?

Nos hemos hecho esa pregunta durante miles de años y aún no hemos podido ponernos de acuerdo.

Porque las matemáticas apuntalan casi todo en nuestro mundo moderno, desde computadoras y teléfonos móviles hasta nuestra comprensión de la biología humana y nuestro lugar en el Universo.

Es por eso que los grandes pensadores de la historia han tratado de explicar los orígenes del extraordinario poder de las matemáticas.

Los números

El mundo moderno no existiría sin las matemáticas. Se esconde detrás de casi todo lo que nos rodea e influye sutilmente casi todo lo que ahora hacemos.

Y, sin embargo, es invisible. Intangible.

Entonces, ¿de dónde vienen las matemáticas? ¿Dónde viven los números?

A menudo pensamos en los números como algo atado a objetos, como el número de dedos en una mano o el número de pétalos en una flor.

Esta flor tiene 5 pétalos. Si le quitas 2, quedarán solo 3 (y se verá menos bonita).

Los pétalos ya no estarán, pero el número 2 seguirá existiendo.

Eso es algo que no puedes decir de todo: si los lápices nunca se hubieran inventado, la idea de un lápiz no existiría.

Puedes destruir el objeto físico, quemarlo hasta que sólo queden cenizas, pero no puedes destruir la idea de los números.

En todas las culturas del mundo, todos estamos de acuerdo sobre el concepto de 4, así lo llames cuatro, four, quatre, vier, o escribas el símbolo de otra manera.

El mundo platónico de los números

¿Habrá entonces algún mundo mágico paralelo en el que viven todas las matemáticas? ¿Un lugar en el que están las verdades fundamentales que nos ayudan a comprender las reglas de la ciencia?

O, ¿será todo producto de nuestra imaginación e intelecto?

«Es demasiado extraordinario pensar que las verdades matemáticas son producto enteramente de nuestras convenciones en la mente humana… Yo no creo que seamos tan inventivos«, opina Eleanor Knox, doctora en Filosofía de la Física de King’s College London, Reino Unido.

«A veces parece que las matemáticas se descubren, especialmente cuando el trabajo va muy bien y sientes como si las ecuaciones te estuvieran impulsando», señala Brian Greene, profesor de Física y Matemáticas de la Universidad de Columbia, EE.UU.

«Pero luego das un paso atrás y te das cuenta de que es el cerebro humano el que impone estas ideas y estos patrones en el mundo y, desde esa perspectiva, parece que las matemáticas son algo que viene de nosotros«, agrega Greene.

«El número cinco se llama fem en sueco, mi lengua materna», dice Max Tegmark, profesor de Física y Matemáticas en MIT, EE.UU.

«Esa parte la inventamos, el bagaje, la descripción, el lenguaje de las matemáticas. Pero la estructura en sí misma, como el número 5 y el hecho de que es 2 + 3, esa es la parte que descubrimos», explica el experto sueco.

El problema es que tanto quienes creen que las matemáticas fueron descubiertas como quienes piensan que son inventadas tienen argumentos muy persuasivos.

Tanto que seguramente esta serie te hará cambiar de opinión una y otra vez.

Para darte una prueba, empecemos con unas de muestras más sencillas de quienes dicen: «Las matemáticas están a nuestro alrededor. Solo necesitas saber dónde mirar para descubrirlas».

El ingenio del nautilino

De todas las estructuras que encuentras en la naturaleza, una de las más bellas es la concha de los nautilinos.

La criatura que vive adentro crea todas estas formas, y salta de una cámara a otra a medida que crece.

Es asombroso cómo ese pequeño ser puede crear algo tan extraordinario e increíblemente complejo.

Además, tiene un patrón oculto, que puedes revelar tomando tres pares de medidas de las cámaras.

Elijes un ángulo y mides la cámara interior, y luego una segunda medición hasta el borde exterior.

Tras hacer eso tres veces en tres ángulos diferentes tendrás tres pares de números que, a primera vista, parecen aleatorios.

En este caso:

• 14,5 / 46,7
• 23,9 / 77,6
• 307 / 995

Pero las apariencias pueden ser engañosas, porque si tomas cada uno de estos pares de números y divides uno por otro, comienza a emerger un patrón muy claro.

• 46,7 dividido 14,5 = 3,2
• 77,6 dividido 23,9 = 3,2
• 995 dividido 307 = 3,2

No importa dónde midas la concha, la proporción del ancho de las cámaras termina siendo constante.

Cada vez que el nautilino hace un giro completo, termina sentado en una cámara que tiene aproximadamente 3,2 veces el ancho del giro anterior.

Y al repetir esta simple regla matemática, puede crear esa concha en espiral bellamente intrincada.

Los pétalos de las flores

El nautilino no es el único ser vivo que tiene un patrón matemático oculto en su interior.

Si alguna vez has contado los pétalos de una flor, es posible que hayas notado algo inusual.

Unas tienen 3 pétalos. Otras, 5. Algunas, 8. Hay de 13 pétalos. Pero rara vez tienen los números intermedios (4, 6, 7, 9, 10, 11 o 12).

Estos números surgen una y otra vez. Parecen aleatorios, pero todos son parte de lo que se llama la secuencia o sucesión de Fibonacci, en nombre del matemático italiano del siglo XIII que la describió en Europa.

Comienzas con los números 1 y 1, y desde ese punto, sigues sumando los dos últimos números.

Así que…

1 + 1 = 2

1 + 2 = 3

2 + 3 = 5

3 + 5 = 8

… y así sucesivamente.

Al observar la cantidad de pétalos en una flor, descubres que siguen la sucesión de Fibonacci. Lo mismo sucede en muchas configuraciones biológicas, como las ramas de los árboles y las hojas en los tallos, entre otras.

Y eso no es todo.

Si te fijas en el centro de un girasol, verás que las semillas están dispuestas en forma de espiral. Cuenta el número de espirales en una dirección y, a menudo, encontrarás un número de Fibonacci.

Si luego cuentas las espirales que van en la dirección opuesta, encontrarás un número de Fibonacci adyacente.

¿Por qué las plantas hacen eso? Pues resulta que es la mejor manera en la que la flor puede organizar sus semillas para evitar que se dañen.

Esas reglas matemáticas simples y gloriosas que se encuentran escondidas en la naturaleza no parecen una coincidencia.

Una vez que detectas este tipo de patrones matemáticos, sientes que los descubriste, no que te los inventaste.

Es como si las matemáticas estuvieran ahí esperando que las encuentres.

No obstante…

Durante siglos, se pensó que el lenguaje de las matemáticas era fijo e inalterable, hasta que se hizo evidente que faltaba algo:

¿Qué es exactamente cero?

Un cero significa nada. Si tienes cero de algo, tienes nada.

El 0 es un concepto extraño; es como si la ausencia se convirtiera en algo.

¿Se trata de un número o una idea? ¿Y cómo puede algo sin valor tener tanto poder?

El 0 vs. los romanos

Aunque siempre hemos entendido el concepto de no tener nada, el concepto de cero es relativamente nuevo.

Usábamos números, podíamos contar pero antes del siglo VII el cero no existía.

Occidente ya tenía un sistema numérico: los números romanos.

Funcionaban bien, aunque eran algo difíciles de manejar

No se sabe si el 0 se originó en China o India pero fue en la última donde se comenzó a aceptar como un número adecuado.

Durante casi 1.000 años, los matemáticos indios trabajaron felices con números indo-arábigos, mientras que sus homólogos occidentales continuaron con los números romanos, hasta que el matemático Fibonacci reconoció su potencial.

Había sido educado en el norte de África, conocía la obra del erudito persa Al-Juarismi, por lo que había visto de primera mano cuán bien funcionaba ese sistema de números.

Es por eso que alertó a Europa occidental de la existencia del sistema indo-arábigo y defendió el 0.

Ese nuevo número era el que más cambios introducía.

En números romanos, por ejemplo, 1958 se escribe: MCMLVIII.

No importa dónde la coloques, la letra C siempre representa el número 100.

El 0 era diferente. Su posición podía cambiar los valores de los números a su alrededor. Piensa en la diferencia entre 11 y 101.

El 0 te permite escribir más números y manipularlos mucho más rápida y fácilmente.

Ahora: el 0 no lo descubrimos, lo creamos como parte del lenguaje para describir números.

Eso hace que las matemáticas se sientan como algo que hemos ideado. Necesitábamos un sistema numérico más fácil de usar así que a alguien se le ocurrió la brillante idea del cero.

Es una evidencia intrigante de que las matemáticas podrían ser inventadas, un producto de nuestro intelecto e imaginación.

Y no es la única, por supuesto, así como hay muchas más que apoyan el argumento de que las matemáticas ya existen y las vamos descubriendo.

¿Qué piensas tú?

*Basado en la serie de la BBC: «Números mágicos: el misterioso mundo de las matemáticas»

Fuente: bbc.com

---

.

.

La importancia de enseñar Ciencias

¿En qué consiste enseñar ciencias?

Por José Sellés-Martínez.

El Galpón de las Ciencias. Despertar vocaciones científicas, el mayor «semillero» para el desarrollo del país.

En 1883, T. H. Huxley se lamentaba de que la literatura se enseñara como si fuera una ciencia, reduciéndola a las reglas ortográficas y gramaticales, y en contrapartida, la ciencia se enseñara como si fuera un poema, recitándola de memoria. La situación no ha variado mucho desde entonces y los estudiantes secundarios, a pesar de contar con una importante carga horaria dedicada a las matemáticas, la física, la química y la biología, terminan sus estudios con muy pocos conocimientos sobre las mismas. Esto es particularmente grave en tanto se sabe que las oportunidades de mejores puestos de trabajo son cada vez más dependientes de los conocimientos y habilidades vinculadas a las ciencias.

En primer lugar debe destacarse que enseñar ciencia no es enseñar fórmulas. Reducir la enseñanza de las ciencias a la retención memorística de fórmulas que resuelven determinados problemas es uno de los errores capitales en la educación. No es frecuente que un docente se detenga a explicar cuáles fueron los razonamientos y las observaciones que permitieron desarrollar la fórmula que resuelve un problema determinado. Sin embargo, esto es primordial para que la educación científica logre sus objetivos.Newsletters Clarín Alberto y Cristina

Comprender el proceso de reflexión y experimentación que llevó a establecer de qué parámetros depende una variable y en qué grado influye cada uno de ellos en la fórmula que los relaciona es lo que contribuye al aprendizaje, no la repetición memorística de la fórmula. Esto, permitirá, además, recordarla con mayor facilidad. Dejará de ser una poesía escrita en un idioma extraño, que se recita por fonética, para comprenderse su significado.

Enseñar ciencia es enseñar por qué cada fórmula es como es y cómo se llegó a ella; la fórmula en sí es secundaria. Una vez descubierta, sólo sirve para resolver una situación que ya ha dejado de ser un problema científico y se ha reducido a un mero reemplazo matemático de términos, de los cuales algunos son datos y otros incógnitas que se resuelven con un simple pasaje de términos.

En segundo lugar puede señalarse que muchas veces se olvida que la historia de la ciencia también es parte de la ciencia. Lamentablemente la poca historia de la ciencia que suele citarse está vinculada a su relación con temas sociales y no al trabajo del investigador. Galileo es más recordado por su enfrentamiento con la iglesia que por sus métodos de trabajo.

Newton es recordado por una anécdota (además falsa) que refiere que fue la caída de una manzana sobre su cabeza lo que le llevó a explorar el concepto de la atracción gravitatoria y no por la forma en que encaró la resolución de problemas. Enseñar cómo se hace la ciencia y qué sienten y cómo reaccionan los científicos cuando llegan a resultados innovadores o cuando sus experimentos fracasan también es enseñar ciencia.

Una tercera actitud que influye negativamente en la formación científica de los ciudadanos es la tendencia a dejar de lado el uso de métodos manuales y tecnologías analógicas y su reemplazo indiscriminado por métodos digitales. Se desprecian métodos tradicionales porque los programas de computadora hacen todo más rápido y lo presentan de modo más atractivo.

Sin embargo, la función pedagógica de ciertos métodos “tecnológicamente anacrónicos” no es reemplazada con el uso indiscriminado de las tecnologías modernas que funcionan como “cajas negras”. La tecnología no tiene el mismo papel en la educación que en la vida cotidiana y esto parece ser olvidado cuando se exige a las escuelas una modernización tecnológica que no está acompañada por la capacitación para el uso sensato de la misma.

El desarrollo de un país va de la mano de su desarrollo científico y tecnológico. Formar científicos e ingenieros que generen nuevos conocimientos que, a su vez, produzcan avances tecnológicos que permitan, por ejemplo, la comercialización de nuevas patentes es un requisito ineludible para el progreso genuino. Es necesario, por lo tanto despertar vocaciones científicas que nutran a las universidades de estudiantes pertrechados con las habilidades, conocimientos e inquietudes necesarios para esa etapa. En una adecuada enseñanza de las ciencias a nivel secundario está la clave del éxito y del fracaso.

José Sellés-Martínez es profesor del Departamento de Ciencias Geológicas, FCEyN – UBA.

Fuente: Clarín, 17/01/20.

---

Vincúlese a nuestras Redes Sociales:  LinkedIn      Twitter

---

.

.