La importancia del Azar: Más allá de un juego de dados
noviembre 17, 2023
Por Gustavo Ibáñez Padilla.
Álea iacta est – la suerte está echada. Estas palabras, atribuidas a Julio César en el crucial momento en que cruzó el río Rubicón, resonaron a lo largo de la historia como un recordatorio de que la vida está impregnada de elementos impredecibles. Hoy, en el siglo XXI, el concepto de azar cobra especial relevancia, por lo que resulta de gran interés explorar su papel en nuestras decisiones y considerar su presencia constante en eventos aparentemente insignificantes.
.
La aleatoriedad, definida como la imprevisibilidad inherente a ciertos eventos, procesos o modelos, encuentra su lugar en diversas disciplinas, desde las matemáticas hasta la filosofía y la física cuántica. En el vasto tablero de la existencia, cada lanzamiento de dados representa un encuentro con lo incierto.
En el ámbito matemático, se plantea una interesante paradoja: solo una secuencia infinita puede considerarse verdaderamente aleatoria. Para secuencias finitas, la influencia de un determinismo subyacente se hace evidente, ya que siempre es posible encontrar una fórmula que las reproduzca. Sin embargo, en la física cuántica, se postula una aleatoriedad profunda, desafiando nuestra capacidad de prever los resultados incluso en eventos macroscópicos como el lanzamiento de dados.
Blaise Pascal, Pierre de Fermat, Christiaan Huygens y Jacob Bernoulli, pioneros en la exploración de la probabilidad, sentaron las bases de lo que hoy conocemos como Teoría de Probabilidad. Estos visionarios matemáticos avanzaron en la comprensión de la aleatoriedad estadística, considerando las frecuencias de bloque como medida de lo impredecible.
.
La historia de la aleatoriedad se entrelaza con la eterna disyuntiva entre el libre albedrío y el determinismo. A lo largo de milenios, la filosofía y la teología han debatido sobre la autonomía de nuestras decisiones frente a un destino predestinado. Es en este diálogo entre lo impredecible y lo inevitable donde la aleatoriedad ocupa un papel crucial.
El término ‘aleatorio’ no solo denota la carencia de propósito, causa u orden, sino que también se asocia con propiedades estadísticas medibles, como la ausencia de tendencias o correlaciones identificables. En este sentido, la aleatoriedad se manifiesta como un fenómeno que trasciende la casualidad, influenciando tanto la ciencia como la historia.
A medida que avanzamos en la comprensión de la aleatoriedad, la Teoría de la información introduce la entropía como una medida de desorden, y los matemáticos Gregory Chaitin, Andréi Kolmogórov y Ray Solomonoff aportan la noción de aleatoriedad algorítmica. En este enfoque, la imprevisibilidad de una secuencia se relaciona con su capacidad para resistir la compresión algorítmica, desafiando la idea de un universo regido por patrones predefinidos. A pesar de ello cabe aquí recordar la frase del genial Albert Einstein: “Dios no juega a los dados”.
.
Pero, ¿cómo afecta el azar a nuestras vidas cotidianas? En situaciones aparentemente mundanas, como elegir una ruta para el trabajo o decidir qué película ver, la aleatoriedad se manifiesta. Tomemos el ejemplo de las aplicaciones de navegación: cada vez que confiamos en ellas para dirigirnos, confiamos en algoritmos que incorporan elementos de azar en la búsqueda de la ruta más eficiente. Detrás de la aparente simplicidad de estas decisiones se encuentra la complejidad de lo impredecible.
Incluso en la toma de decisiones más trascendentales, como elegir una carrera o a la pareja de vida, la influencia del azar no puede subestimarse. La vida está llena de giros inesperados, encuentros fortuitos y oportunidades que surgen sin previo aviso. En palabras de Nassim Taleb, autor de El Cisne Negro, la vida está llena de eventos altamente improbables que desafían nuestras expectativas y definen nuestro destino.
.
En última instancia, la importancia del azar en nuestra vida radica en su capacidad para desafiar nuestras certezas y abrir puertas a lo inexplorado. Al reconocer la presencia constante de la aleatoriedad, podemos abrazar la incertidumbre como parte integral de nuestra existencia. Cada paso que damos, cada decisión que tomamos, se convierte en una apuesta contra las probabilidades, recordándonos que, al igual que Julio César al cruzar el Rubicón, estamos echando el dado de la vida.
En un mundo cada vez más complejo e interconectado, la comprensión de la aleatoriedad se convierte en una herramienta invaluable. Nos permite adaptarnos a lo inesperado, encontrar oportunidades en los desafíos y abrazar la diversidad de experiencias que la vida tiene para ofrecer. En última instancia, la suerte puede estar echada, pero cómo enfrentamos la incertidumbre y aprovechamos las oportunidades que se presentan es el verdadero juego que define nuestra historia.
Fuente: Ediciones EP, 17/11/23.
Información sobre Gustavo Ibáñez Padilla
Más información:
Matemáticas y juegos de azar
Medidas de Tendencia Central en el Mundo Financiero
La Regresión a la Media y la Ley de los Grandes Números: Su Impacto en las Finanzas y la Gestión del Riesgo
.
.
La Regresión a la Media y la Ley de los Grandes Números: Su Impacto en las Finanzas y la Gestión del Riesgo
octubre 13, 2023
Por Gustavo Ibáñez Padilla.
En el complejo universo de las finanzas e inversiones, comprender las sutilezas estadísticas es crucial para tomar decisiones acertadas. Dos conceptos fundamentales que destacan en este panorama son la Regresión a la Media y la Ley de los Grandes Números, principios respaldados por la experiencia de matemáticos, expertos y empresarios de renombre. Reflexionaremos más a fondo en estos conceptos y su aplicación en finanzas, inversión y, crucialmente, en la Gestión del Riesgo y los Seguros, resaltando así la importancia de la Protección Financiera en la vida de todo empresario o inversor.
Regresión a la Media
La Regresión a la Media, propuesta por el visionario Francis Galton, nos recuerda que los resultados extremos tienden a equilibrarse con el tiempo. Esto tiene una aplicación vital en la Gestión del Riesgo y los Seguros. En palabras de Nassim Taleb, el reconocido autor de El Cisne Negro: “La Regresión a la Media es el alma de la gestión del riesgo.”
Supongamos un empresario que dirige una cadena de restaurantes. Después de un año excepcionalmente rentable, es sabio no asumir que este nivel de ganancias continuará indefinidamente. La Regresión a la Media sugiere que es más probable que las ganancias se estabilicen o disminuyan en el próximo período contable. Aquí, la Protección Financiera, en forma de reservas o seguros empresariales, puede ser la diferencia entre la continuidad del negocio y la crisis financiera ante una caída inesperada en las ganancias.
“Entender la Regresión a la Media es crucial para gestionar el riesgo. Es la base de cualquier sistema de seguro o protección financiera” nos recuerda el matemático y bróker de inversionesNassim Taleb.
Ley de los Grandes Números
La Ley de los Grandes Números ─formulada por el genial matemático suizo Jakob Bernoulli, en su obra Ars Conjectandi del siglo XVIII─ establece que a medida que se realizan un número creciente de experimentos o eventos independientes, la media de los resultados se aproximará al valor esperado o teórico. Esta ley es esencial para comprender cómo los resultados a corto plazo pueden variar significativamente de las tendencias a largo plazo.
.
Imaginemos un fondo de inversión que invierte en una amplia variedad de activos. Durante un trimestre, algunos activos pueden experimentar pérdidas, pero la cartera en su conjunto tiene una tendencia positiva. La Ley de los Grandes Números nos asegura que, a medida que se acumulan más trimestres, la rentabilidad promedio de la cartera se aproximará a la expectativa teórica.
El meollo de la cuestión se sintetiza en la siguiente afirmación de Jakob Bernoulli: “La aritmética de los acontecimientos inciertos es tan exacta como la de la certeza.”
La Ley de los Grandes Números es también el pilar de la industria de los Seguros. A medida que la cartera de asegurados se amplía, las compañías aseguradoras pueden prever con mayor precisión los eventos y establecer primas adecuadas.
Consideremos una compañía de seguros de salud. Al tener un gran número de asegurados, la compañía puede prever con alta certeza la cantidad de reclamaciones médicas que recibirán en un periodo determinado. Esto les permite fijar primas que cubran los costos, generando así beneficios tanto para la compañía como para los asegurados.
La certeza que nos brinda esta ley es refrendada por Warren Buffett, cuando dice: “La Ley de los Grandes Números es el fundamento de la industria de seguros. Nos permite entender y gestionar el riesgo.”
.
Aplicaciones en el Mundo de las Inversiones
Estos conceptos tienen un impacto sustancial en las decisiones de inversión y gestión de carteras:
- Selección de Activos: La Regresión a la Media advierte a los inversores sobre la posible reversión de tendencias extremas en el corto plazo.
- Diversificación y Gestión del Riesgo: La Ley de los Grandes Números respalda la estrategia de diversificación como una forma efectiva de mitigar el riesgo.
- Planificación a Largo Plazo: Ambos conceptos son esenciales para la toma de decisiones a largo plazo, permitiendo a los inversores evitar reacciones impulsivas a fluctuaciones temporales.
Especulación y Protección Financiera
Los especuladores exitosos, como George Soros, reconocen la importancia de la Protección Financiera. Soros, famoso por su papel en la caída de la libra esterlina en 1992, no solo especuló, sino que también utilizó estrategias de protección para mitigar el riesgo asociado con sus posiciones.
Imaginemos a un inversor que ha identificado una oportunidad de inversión en una nueva empresa tecnológica. Si bien está entusiasmado con el potencial de crecimiento, también es consciente de los riesgos inherentes a las startups. Aquí, la adopción de estrategias de Protección Financiera, como la diversificación de la cartera, puede ser crucial para mitigar el riesgo asociado con este tipo de inversiones más volátiles.
Siempre debemos recordar la recomendación de Nassim Taleb: “La Protección Financiera no es solo una estrategia, es una filosofía de vida. Permite a los inversores prosperar en la incertidumbre.”
Regresión a la Media y Ley de los Grandes Números como bases del éxito
La combinación de la Regresión a la Media y la Ley de los Grandes Números forma la base de decisiones financieras informadas y la gestión eficaz del riesgo. En un mundo mundo Volátil, Incierto, Complejo y Ambiguo, la Protección Financiera se convierte en una herramienta invaluable para asegurar la continuidad y el éxito en cualquier empresa o cartera de inversión. Como afirmó Warren Buffett, “la inversión exitosa es sobre la gestión del riesgo, no su eliminación.”
Al comprender y aplicar estos fundamentales conceptos, los empresarios, los inversores, los gestores de riesgos y las personas en general pueden desempeñarse con confianza en el cambiante escenario financiero, construyendo un futuro económico de mayor estabilidad y prosperidad.
Fuente: Ediciones EP, octubre 2023.
Más información:
Medidas de Tendencia Central en el Mundo Financiero
.
.
Medidas de Tendencia Central en el Mundo Financiero
octubre 12, 2023
Por Gustavo Ibáñez Padilla.
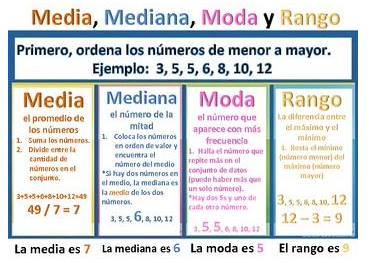
En el dinámico mundo de las finanzas, la clave para tomar decisiones acertadas radica en la capacidad de interpretar y analizar datos de manera rápida y efectiva. En este sentido, las Medidas de tendencia central estadística son herramientas fundamentales. La media, mediana, moda y rango son como brújulas que nos orientan en el vasto océano de la información financiera. Son parámetros estadísticos simples que indican cuál es el centro de un conjunto de datos. Su uso está muy difundido, ya que al resumir un conjunto de datos en un solo valor simplifican el análisis de todo un bloque de información y proporcionan una visión generalizada sobre el mismo.
.
Principales medidas de tendencia central
─La Media: Equilibrio en los Ingresos
La media, también conocida como promedio, es el punto de equilibrio de un conjunto de datos. Es el resultado de sumar todos los valores y luego dividirlos por la cantidad de elementos. Para visualizarlo, imaginemos un grupo de diez profesionales con diferentes niveles de ingresos. Si sumamos todos los sueldos y los dividimos entre diez, obtendremos la media de ingresos del grupo.
Es importante tener en cuenta que la media puede ser influenciada por valores extremos. Si uno de los profesionales tiene un sueldo excepcionalmente alto, este valor puede distorsionar la media y no reflejar la situación financiera real del grupo en su conjunto.
─La Mediana: Estabilidad en los ingresos
A diferencia de la media, la mediana es el valor intermedio de un grupo de números. Se trata del valor que se encuentra en el centro de un conjunto de datos ordenados. Imaginemos un grupo de nueve ejecutivos, esta vez ordenados por sus ingresos de menor a mayor. La mediana será el sueldo del quinto profesional en esta lista.
Lo destacado de la mediana es su resistencia a los valores atípicos. Esto la convierte en una herramienta valiosa para evaluar la estabilidad financiera del grupo. Si uno de los profesionales tiene un ingreso muy alto o muy bajo, la mediana no se ve afectada en la misma medida que la media.
─La Moda: El Favorito en los ingresos
La moda es el valor más frecuente en un conjunto de datos. Es como el favorito de la multitud. Siguiendo con el ejemplo de los ingresos, si cierto sueldo es el más repetido en el grupo de profesionales, entonces ese valor es la moda.
Para ilustrar este punto, imaginemos que en el grupo de diez ejecutivos, cinco de ellos tienen el mismo sueldo mensual. En este caso, ese sueldo específico se convierte en la moda. Esto puede indicar tendencias en los salarios de la industria o en la empresa en la que trabajan.
─El Rango: Variedad en los ingresos
El rango es la diferencia entre el valor más alto y el más bajo en un conjunto de datos. Nos brinda una visión clara de la variedad de resultados posibles. Continuando con el ejemplo de los profesionales, si el ingreso más alto es de U$S100.000 y el más bajo es de U$S30.000, el rango sería de U$S70.000. Esto nos indica que existe una amplia gama de ingresos en el grupo.
En el mundo financiero, el rango es una herramienta esencial para evaluar la volatilidad y el nivel de riesgo asociado a ciertos activos o inversiones. Un rango amplio sugiere una mayor variabilidad en los resultados y, por lo tanto, un mayor nivel de riesgo.
.
El valor de las medidas de tendencia central
Para respaldar la importancia de estos parámetros, el matemático John Allen Paulos señaló: «En un mundo inundado de datos, las medidas de tendencia central son faros que nos guían hacia decisiones más certeras.»
El famoso economista John Maynard Keynes también subrayó la relevancia de estas herramientas al afirmar: «Sin una comprensión profunda de las tendencias centrales de los datos, las decisiones económicas carecen de fundamento sólido.»
Tomando el timón de tus finanzas
Al aplicar estas medidas de tendencia central en el mundo financiero, te empoderas para tomar decisiones más inteligentes y adaptativas. Imagina que estás considerando invertir en dos fondos mutuos. Al analizar sus historiales de rendimiento, puedes usar la mediana para evaluar la estabilidad y la moda para identificar cuál ha sido el favorito del mercado. El rango te proporciona información sobre la variabilidad y el riesgo asociado a cada fondo.
En última instancia, al comprender y aplicar estas herramientas, estás tomando el timón de tus finanzas. No te limitas a navegar por el mar de datos, sino que tienes el poder de dirigir tu curso hacia un futuro financiero más próspero y seguro. Como dijo Martin Gardner, «la comprensión de las tendencias centrales nos brinda una brújula confiable en el laberinto de la información financiera.» ¡Así que adelante, fija el rumbo y emprende tu ruta hacia el éxito financiero!
Fuente: Ediciones EP, 11/10/23.
.
.
Para saber más sobre Big Data
mayo 9, 2020
Big Data. Conceptos, tecnologías y aplicaciones
El libro que tengo en las manos es una excelente aportación para el conocimiento del público en general del gran paradigma que conmueve los cimientos de nuestro mundo, el Big Data. Se trata de Big Data. Conceptos, tecnologías y aplicaciones, en la colección Qué sabemos de, escrito por dos expertos, David Ríos Insúa y David Gómez Ullate.
Comentaremos brevemente el contenido de este libro, aunque en entradas sucesivas seguiremos hablando de algunos de los temas que, al menos a mí, me han resultado tan interesantes como para querer saber más sobre ellos.
Una de las cuestiones más preocupantes del big data es que una gran parte de ese tsunami de datos lo estamos proporcionando nosotros mismos de manera gratuita y casi sin darnos cuenta, como si no nos importara. Y con esos datos, hay compañías que hacen negocios. Google recibe 4 millones de peticiones por minuto, en Facebook compartimos 2 millones y medio de piezas por minuto, cada día enviamos 400 millones de tuits.
La importancia de los datos y su análisis tiene un origen comercial, como conocer mejor a los clientes, sus gustos, como llegar mejor a ellos. Y si antiguamente (por ejemplo, Gallup) había que hacer encuestas, los avances tecnológicos (internet, móviles, GPS, …) han facilitado la tarea. Se dice que hay unos 15.000 millones de sensores distribuidos en el mundo, y no paran,
Pero estos datos se dan en bruto, tenemos que pulirlos y almacernarlos para poder usarlos. Y después tenemos que aplicar diferentes tecnologías para extraer información útil de los mismos. Y ahí es donde entran las matemáticas. Los autores muestran como una de las bases claves es la Estadística. El otro pilar es la Infomática. A lo largo del libro describen ampliamente como estas dos disciplinas interactúan en el Big Data. Y ello les lleva a hablar del aprendizaje automático (machine learning), redes neuronales, inteligencia artificial, ciberseguridad, y muchos otros temas.
Es muy relevante como las administraciones públicas están tan lejos de las grandes corporaciones empresariales y no están utilizando estas nuevas herramientas en beneficio de la sociedad; hay un enorme potencial en su uso, por ejemplo, en la medicina, tal y como detallan en uno de sus capítulos.
Aunque a veces la lectura nos produce el temor al Gran Hermano, los aspectos positivos son muchos, como ocurre casi siempre con la ciencia. El Big Data no es la panacea a todos los problemas de este mundo pero si que nos ofrece un gran cantidad de oportunidades. Enhorabuena a los autores por este magnífico libro que en apenas 134 páginas no nos da respiro.
David Ríos Insúa. Es AXA-ICMAT Chair en Análisis de Riesgos Adversarios en el ICMAT-CSIC y numerario de la Real Academia de Ciencias Exactas, Físicas y Naturales. Es catedrático de Estadística e Investigación Operativa (en excedencia). Previamente ha sido profesor o investigador en Manchester, Leeds, Duke, Purdue, Paris-Dauphine, Aalto, CNR-IMATI, IIASA, SAMSI y UPM. Entre otros, ha recibido el Premio DeGroot de la ISBA por su libro Adversarial Risk Analysis. Es asesor científico de Aisoy Robotics. Ha escrito más de 130 artículos con revisión y 15 monografías sobre sus temas de interés que incluyen la inferencia bayesiana, la ciencia de datos, el análisis de decisiones y el análisis de riesgos, y sus aplicaciones, principalmente, a seguridad y ciberseguridad.
David Gómez-Ullate Oteiza. Es investigador en la Universidad de Cádiz y profesor titular de Matemática Aplicada en la Universidad Complutense de Madrid. Su labor reciente se centra en la transferencia de conocimiento al sector industrial en ciencia de datos e inteligencia artificial. Dirige proyectos en el sector aeronáutico, seguros y biomédico aplicando técnicas de visión artificial y procesamiento de lenguaje natural.
___
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).
Fuente: madrimasd.org, 2020.
Vincúlese a nuestras Redes Sociales:
LinkedIn YouTube Facebook Twitter
.
.
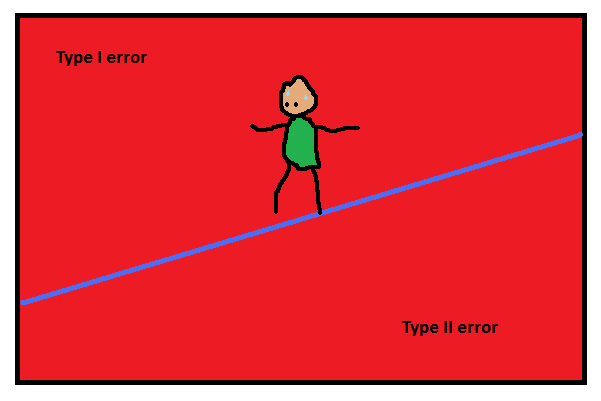
Estadística: ¿Cuál error es peor: Tipo I o Tipo II?
octubre 26, 2018
¿Qué tipo de error estadístico es peor: Tipo I o Tipo II?
Por Eston Martz.
La gente puede cometer errores cuando realiza un test de hipótesis con análisis estadísticos. Específicamente, pueden hacer errores de Tipo I o Tipo II.
A medida que se analizan los propios datos y se hacen test de las hipótesis, la comprensión de la diferencia entre los errores de Tipo I y Tipo II se convierte en algo extremadamente importante, porque existe un riesgo de cometer cada tipo de error en cada análisis, y la cantidad del riesgo está bajo nuestro control.
Así que si se está testeando una hipótesis sobre un asunto de seguridad o calidad que podría afectar a la vida de las personas, o un proyecto que podría ahorrar millones de dólares a su negocio, ¿qué tipo de error tendría consecuencias más serias o más costosas? ¿Existe un tipo de error que sea más importante de controlar que otro?
Antes de que intentemos contestar a esta pregunta, revisemos qué son estos errores.
La hipótesis nula y los errores de Tipo I y II
Cuando los estadísticos se refieren a errores de Tipo I y Tipo II, nos referimos a las dos maneras en que se pueden realizar errores respecto a la hipótesis nula (Ho). La hipótesis nula es la posición por defecto, semejante a la idea de “inocencia hasta que se pruebe la culpabilidad”. Cualquier test de hipótesis se empieza con la asunción de que la hipótesis nula es correcta.
Cometemos un error de Tipo I si rechazamos la hipótesis nula cuando ésta es cierta. Se trata de un falso positivo, como una alarma de fuego que suena cuando no existe tal fuego.
Un error de Tipo II ocurre si nos equivocamos al rechazar el nulo cuando no es cierto. Es el caso de un falso negativo—como una alarma que falla y no suena cuando existe un fuego.
Es más fácil de comprenderlo en la tabla siguiente, semejante a la que se puede encontrar en cada texto sobre estadística:
| Realidad | Hipótesis nula (H0) no rechazada | Hipótesis nula (H0) rechazada |
| H0 es cierta. | Conclusión correcta. | Error Tipo I (falso positivo) |
| H0 es falsa. | Error Tipo II (falso negativo) | Conclusión correcta. |
Estos errores están relacionados con los conceptos estadísticos de riesgo, significancia y potencia.
.
.
Reducir el riesgo de errores estadísticos
Los estadísticos llaman al riesgo, o probabilidad, de cometer un error de Tipo I “alfa,” igual que el “nivel de significación”. En otras palabras, es la voluntad de arriesgarse rechazando la hipótesis nula cuando es cierta. Alfa normalmente se pone a 0,05, que es una posibilidad del 5 por ciento de rechazar la hipótesis nula cuando es cierta. Cuanto más pequeña sea alfa, menor es el riesgo de rechazar la hipótesis nula incorrectamente. En situaciones de vida o muerte, por ejemplo, una alfa de 0.01 reduce la probabilidad de un error Tipo I a justo un 1 por ciento.
Un error de Tipo II está relacionado con el concepto de “potencia”, y la probabilidad de cometer este error se refiere como “beta”. Podemos reducir nuestro riesgo de cometer un error Tipo II asegurando que nuestro test tiene suficiente potencia—lo que depende de si el tamaño de la muestra es suficientemente grande para detectar una diferencia cuando ésta existe.
El argumento por defecto para «Qué error es peor»
Volvamos a la cuestión de qué error, Tipo I o Tipo II, es peor. El ejemplo de referencia para ayudar a la gente a pensar sobre el tema es un acusado de un crimen que exige una sentencia muy dura.
La hipótesis nula es que el acusado es inocente. Por supuesto no se querrá librar a una persona culpable de la cárcel, pero la mayoría de la gente diría que sentenciar a una persona inocente a esa pena es una consecuencia todavía peor.
Por lo tanto, muchos textos e instructores dirán que el Tipo I (falso positivo) es peor que un error Tipo II (falso negativo). La razón se reduce a la idea que si se mantiene el status quo o asunción por defecto, al menos no se estará haciendo las cosas peor.
Y en muchos casos, eso es cierto. Pero como pasa tanto en estadística, en la aplicación nada es realmente tan blanco o negro. La analogía del acusado es muy Buena para enseñar el concepto, pero cuando se intenta hacer una regla de oro sobre qué tipo de error es peor en la práctica, se desmorona.
Pero entonces, ¿qué tipo de error es el peor?
Siento decepcionar, pero como en tantas cosas de la vida y la estadística, la respuesta más honesta a esta pregunta tiene que ser, “depende”.
En alguna situación, el error de Tipo I puede tener consecuencias menos aceptables que las que tendría un error de Tipo II. En otras, el error Tipo II podría ser menos costosos que un error Tipo I. Y, a veces, como Dan Smith indicó en Significance hace unos años, respecto a Seis Sigma y mejora de calidad, «ninguno» es la única respuesta a qué error es el peor:
La mayoría de estudiantes de Seis Sigma van a utilizar los conceptos que aprenden en el contexto de los negocios. En las empresas, cuando le cuestas a la compañía 3 millones de dólares por sugerirle un proceso alternativo cuando no hay nada de malo con el proceso actual o dejas de tener en cuenta 3 millones de dólares de ganancias cuando deberías cambiar a un nuevo proceso pero te equivocas, el resultado final es el mismo. La empresa pierde la posibilidad de obtener un beneficio adicional de 3 millones de dólares.
Mira a las potenciales consecuencias
Como no existe una regla de oro clara sobre qué tipos de errores, Tipo I o Tipo II, son peores, nuestra mejor opción al utilizar datos para verificar una hipótesis es mirar cuidadosamente a las consecuencias que podrían seguir a ambos tipos de errores. Varios expertos sugieren utilizar una tabla como la siguiente para detallar las consecuencias para un error del Tipo I y del Tipo II, en el análisis particular.
| Nula | Error tipo I: H0verdadero, pero rechazado | Error tipo II: H0falso, pero no rechazado |
| Medicina A no alivia la Condición B. | Medicina A no alivia la Condición B, pero no se elimina como opción de tratamiento. | Medicina A alivia la Condición B, pero es eliminada como opción de tratamiento. |
| Consecuencias | Los pacientes con Condición B, que reciben la medicina A no se alivian. Pueden experimentar empeoramiento y/o efectos secundarios hasta incluso morir. Posible litigio. | Un tratamiento viable permanece inaccesible a pacientes con Condición B. Se pierden los costes del desarrollo. Provecho potencial eliminado. |
Sea lo que sea lo que involucre el análisis, comprender la diferencia entre los errores de Tipo I y Tipo II, y considerar y mitigar sus respectivos riesgos como apropiados, siempre es inteligente. Para cada tipo de error, hay que asegurarse de que se responde esta pregunta: «¿Qué es lo peor que puede ocurrir?»
Para explorar este tema más extensamente, compruebe este artículo sobre el uso de cálculo de potencia y tamaño de la muestra para equilibrar el riesgo de un error de tipo II y los costes de la comprobación, o esta entrada del blog sobre considerar el alfa apropiado para su test particular.
Fuente: addlink.es
Más información:
Gonick y Smith. La estadística en comic (cap. 8)
H0 = No hay embarazo. Ha = Sí hay embarazo.
Vincúlese a nuestras Redes Sociales:
Google+ LinkedIn YouTube Facebook Twitter
.
.
.
Moneyball, el juego de la fortuna. Un caso de Inteligencia de Negocios.
septiembre 3, 2018
Moneyball
Fuente: https://youtu.be/Uwg5SjH-f2g – Estadística para Administración
.
Moneyball es una película de 2011 dirigida por Bennett Miller y protagonizada por Brad Pitt, Jonah Hill y Philip Seymour Hoffman. Es una adaptación de la novela Moneyball: the art of winning an unfair game (2003), basada en la historia real de Billy Beane, gerente general del equipo Oakland Athletics, quien utilizaba las estadísticas avanzadas para fichar jugadores.
Es un buen ejemplo de Inteligencia de Negocios (business intelligence).
Sinopsis
Billy Beane (Brad Pitt) es el gerente general del equipo de béisbol Oakland Athletics, que acaba de perder otra temporada más. Decidido a relanzar el equipo, y con la ayuda del joven economista Peter Brand (Jonah Hill), utilizará las estadísticas de este para fichar a los jugadores que cree más oportunos. Un método que no es compartido por sus compañeros, ni por el entrenador del equipo Art Howe (Philip Seymour Hoffman).
Argumento detallado
El gerente general de los Athletics de Oakland, Billy Beane (Brad Pitt), está molesto por la derrota de su equipo ante los Yankees de Nueva York en la postemporada del 2001. Con la inminente perdida de los jugadores estrella Johnny Damon, Jason Giambi, y Jason Isringhausen a agencia libre, Beane trata de diseñar una estrategia para armar un equipo competitivo para el 2002, pero se esfuerza por superar la nómina de jugadores limitados de Oakland. Durante una visita a los Indians de Cleveland, Beane se encuentra con Peter Brand (Jonah Hill), un joven economista graduado en Yale con ideas radicales sobre la forma de evaluar a los jugadores. Beane prueba la teoría de Brand al preguntarle si lo habría fichado (apenas salido de la escuela secundaria); Beane había sido jugador en las Grandes Ligas antes de convertirse en mánager general. Aunque los scouts consideraban a Beane un jugador fenomenal, su carrera en las Grandes Ligas fue decepcionante. Después de cierto estímulo, Brand admite que él no lo habría fichado hasta la novena ronda y que Beane probablemente debería haber aceptado una beca para estudiar en Stanford en su lugar.
Los cazatalentos del equipo son los primeros desconfiados por nuevo enfoque de Brand, sobre todo Grady Fuson – quien es despedido por Beane después de discutir con él a causa del nuevo rumbo deportivo del equipo; después critica en los medios de comunicación las decisiones tomadas por Beane y pone en duda el futuro del equipo. En lugar de basarse en la experiencia de los cazatalentos y la intuición, Brand selecciona a jugadores basados casi exclusivamente en su porcentaje de base (OBP). Al encontrar a los jugadores con un alto OBP pero con características que conducen a los cazatalentos a despedirlos, Brand reúne a un equipo de jugadores infravalorados con mucho más potencial del que se les reconoce y a un precio mucho más económico que las grandes estrellas. A pesar de las vehementes objeciones de los cazatalentos, Beane apoya la teoría de Brand y contrata a los jugadores que seleccionó, como el heterodoxo lanzador submarino Chad Bradford (Casey Bond). Tras los fichajes de agentes libres, Beane se da cuenta que también se enfrenta a la oposición de Art Howe (Philip Seymour Hoffman), mánager de los Athletics. Con las tensiones ya elevadas entre ellos a causa de una disputa contractual, Howe no tiene en cuenta la estrategia de Beane y Brand, y juega el equipo en un estilo tradicional, sin tener en cuenta las indicaciones de Beane.
A principios de la temporada, a los Athletics les va mal, por lo que Beane es fuertemente criticado y ya vaticinan el fracaso del nuevo modelo y su despido como gerente general. Beane convence al propietario a mantener el rumbo, y con el tiempo el equipo comienza a mejorar. En última instancia, los Athletics ganan 20 partidos consecutivos, estableciendo el récord de la Liga americana. Su racha se limita con una victoria sobre los Royals de Kansas City. Al igual que muchos jugadores de béisbol, Beane es supersticioso y evita asistir a los partidos. Su hija le implora que vaya al partido que supondría la victoria número 20 consecutiva contra los Royals, donde Oakland ya gana 11-0 después de la tercera entrada. Beane llega en la cuarta entrada, solo para ver que el equipo va a desintegrarse y, finalmente, permite a los Royals de igualar el marcador 11-11. Por último, los Athletics ganan, con un home-run en la última entrada por una de las selecciones de Brand, Scott Hatterberg. A pesar de todos sus éxitos en la segunda mitad de la temporada, los Ahletics pierden en la primera ronda de la postemporada, esta vez contra los Twins de Minnesota. Beane está decepcionado, pero satisfecho de haber demostrado el valor de los métodos de Brand. Beane se reúne más tarde con el propietario de los Red Sox de Boston, que se da cuenta de que el nuevo modelo utilizado por Beane es el futuro del béisbol, y se ofrece a contratar a Beane como gerente general de los Red Sox.
Para terminar, una nota de la película dice que Beane dejó pasar la oportunidad de convertirse en el gerente general de los Red Sox de Boston, a pesar de una oferta de un salario de 12,5 millones de dólares, lo que lo habría convertido en el gerente general mejor pagado en la historia del deporte. Regresa a Oakland para seguir administrando a los Oakland Athletics. Mientras tanto, dos años después de la adopción de la filosofía de fichajes utilizada en Oakland, los Red Sox de Boston ganan su primera Serie Mundial desde 1918.
Fuente: Wikipedia, 2018.
Vincúlese a nuestras Redes Sociales:
Google+ LinkedIn YouTube Facebook Twitter
.
.