La hipótesis de Riemann, ¿resuelta?
noviembre 18, 2015
Un profesor asegura haber resuelto un problema matemático de 156 años
La hipótesis de Riemann. El nigeriano Opeyemi Enoch afirma haber llegado al resultado. Trabajó durante cinco años en el problema. Pero llevara varios años determinar si efectivamente lo resolvió. De ser correcto, se ganará un premio de un millón de dólares.

El profesor nigenirano Opeyemi Enoch, quien habría resuelto el problema matermático de la hipótesis de Riemann.
Un profesor nigeriano asegura haber resuelto uno de los problemas matemáticos del siglo y podría hacerse acreedor de un premio de un millón de dólares. Se trata de la hipótesis de Riemann, que fue planteada por primera vez en 1859 por el académico Bernhard Riemann, y forma parte de uno de los siete problemas matemáticos del milenio.
Ahora, el Instituto Clay de Matemáticas deberá determinar si el resultado es el correcto y, de ser así, le otorgaría el premio de un millón de dólares al profesor Opeyemi Enoch.
Según cuenta el profesor, a lo largo de estos cinco años hubo dos momentos clave, en los que intuyó que estaba cerca del resultado. «Uno fue en una mañana de 2010, cuando di con el vínculo del problema. Ahí supe que me estaba acercando mucho», cuenta. Luego, continúa, encontró la forma de aplicar lo que había descubierto hasta entonces.
Ahora, el Instituto Clay debe revisar el trabajo de Enoch y dictar un «veredicto». Sin embargo, eso llevará su tiempo. En las reglas que publica el Instituto Clay para dar por resuelto el problema y otorgar el premio, se encuentran las siguientes condiciones: la solución debe haber sido publicada por alguna revista de reputación mundial; la solución debe tener aceptación por parte de la comunidad matemática dos años después. Y recién pasados esos dos años, el instituto tomará una decisión.
La hipótesis de Riemann es uno de los siete problemas matemáticos del milenio. De esos siete problemas ya fue resuelto uno. El de Riemann sería el segundo. Y aún quedan por resolver otros cinco problemas.
Fuente: clarin.com, 18/11/15.
Ver una opinión en contrario:
La supuesta demostración del nigeriano Enoch de la hipótesis de Riemann
Vincúlese a nuestras Redes Sociales:
Google+ LinkedIn YouTube Facebook Twitter
Hipótesis de Riemann
 En matemática pura, la hipótesis de Riemann, formulada por primera vez por Bernhard Riemann en 1859, es una conjetura sobre la distribución de los ceros de la función dseta de Riemann ζ(s).1
En matemática pura, la hipótesis de Riemann, formulada por primera vez por Bernhard Riemann en 1859, es una conjetura sobre la distribución de los ceros de la función dseta de Riemann ζ(s).1
La hipótesis de Riemann, por su relación con la distribución de los números primos en el conjunto de los naturales, es uno de los problemas abiertos más importantes en la matemática contemporánea.
El Instituto Clay de Matemáticas ha ofrecido un premio de un millón de dólares a la primera persona que desarrolle una demostración correcta de la conjetura.2 La mayor parte de la comunidad matemática piensa que la conjetura es correcta, aunque otros grandes matemáticos como J. E. Littlewood y Atle Selberg se han mostrado escépticos, si bien el escepticismo de Selberg fue disminuyendo desde sus días de juventud. En un artículo en 1989 sugirió que un análogo debe ser cierto para una clase mucho más amplia de funciones (la clase de Selberg).
El profesor nigeriano Opeyemi Enoch, quien trabaja en la Universidad Federal de Oye Ekiti en Nigeria, aparentemente ha resuelto el problema de Riemann; el instituto Clay debe hacer la revisión respectiva para confirmar la solución propuesta, según despacho de BBC Mundo del 17 de Noviembre de 2.015: «El profesor que asegura haber resuelto un problema matemático de más de 150 años»..
Definición
La función dseta de Riemann ζ(s) está definida de la siguiente manera:
Para todos los números complejos s ≠ 1, se puede prolongar analíticamente mediante la ecuación funcional:
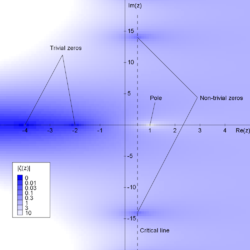
Esta posee ciertos valores, llamados ceros «triviales» para los cuales la función zeta se anula. De la ecuación se puede ver que s = −2, s = −4, s = −6, … son ceros triviales. Existen otros valores complejos s comprendidos entre 0 < Re(s) < 1, para los cuales la función zeta también se anula, llamados ceros «no triviales». La conjetura de Riemann hace referencia a estos ceros no triviales afirmando:
|
Por lo tanto los ceros no triviales deberían encontrarse en la línea crítica s = 1/2 + i t donde t es un número real e i es la unidad imaginaria. La función zeta de Riemann, a lo largo de la línea crítica ha sido estudiada en términos de la función Z, cuyos ceros corresponden a los ceros de la función zeta sobre la línea crítica.
Recordemos lo que en su memoria Riemann afirma.
1º- :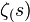 tiene infinitos ceros complejos que estan en la linea recta. Re
tiene infinitos ceros complejos que estan en la linea recta. Re 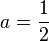
y lm s = 0.
2º- Es muy probable que la raiz de una función x son reales.
Es decir  ; (
; (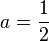 ;
; 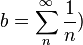 .
.
Esto lo ha demostrado la matemática Albana Diez3 para: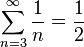
:
Indico una de las series para 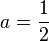 ; no solo existen para este valor, tambien para
; no solo existen para este valor, tambien para 
Historia
Riemann mencionó la conjetura en 1859, que sería llamada la hipótesis de Riemann, en su tesis de doctorado Sobre los números primos menores que una magnitud dada, al desarrollar una fórmula explícita para calcular la cantidad de primos menores que x. Puesto que no era esencial para el propósito central de su artículo, no intentó dar una demostración de la misma. Riemann sabía que los ceros no triviales de la función zeta están distribuidos en torno a la recta s = 1/2 + i t, y sabía también que todos los ceros no triviales debían estar en el rango 0 ≤ Re(s) ≤ 1.4
En 1896, Hadamard y de la Vallée-Poussin probaron independientemente, que ningún cero podía estar sobre la recta Re(s) = 1. Junto con las otras propiedades de los ceros no triviales demostradas por Riemann, esto mostró que todos los ceros no triviales deben estar en el interior de la banda crítica 0 < Re(s) < 1. Este fue un paso fundamental para las primeras demostraciones del teorema de los números primos.
En 1900, Hilbert incluyó la hipótesis de Riemann en su famosa lista de los 23 problemas no resueltos — es parte del problema 8 en la lista de Hilbert junto con la conjetura de Goldbach. Cuando se le preguntó qué haría si se despertara habiendo dormido quinientos años, remarcablemente Hilbert contestó que su primera pregunta sería si la hipótesis de Riemann había sido probada. La hipótesis de Riemann es el único problema de los que propuso Hilbert que está en el premio del milenio del Instituto Clay de Matemáticas.
En 1914, Hardy demostró que existe un número infinito de ceros sobre la recta crítica Re(s) = 1/2. Sin embargo todavía era posible que un número infinito (y posiblemente la mayoría) de los ceros no triviales se encontraran en algún otro lugar sobre la banda crítica. En trabajos posteriores de Hardy y Littlewood en 1921 y de Selberg en 1942 se dieron estimaciones para la densidad promedio de los ceros sobre la línea crítica.
Trabajos recientes se han concentrado en el cálculo explícito de la localización de grandes cantidades de ceros (con la esperanza de hallar algún contraejemplo) y en el establecimiento de cotas superiores en la proporción de ceros que puedan estar lejos de la línea crítica (con la esperanza de reducirlas a cero).
La hipótesis de Riemann y los números primos
La formulación tradicional de la hipótesis de Riemann oscurece un poco la importancia real de la conjetura. La función zeta de Riemann tiene una profunda conexión con los números primos y Hege von Koch demostró en 1901 que la hipótesis de Riemann es equivalente al considerable refinamiento del teorema de los números primos: Existe una constante C > 0 tal que
para todo x suficientemente grande, donde π(x) es la función contadora de primos y ln(x) es el logaritmo natural de x. Lowell Schoenfeld mostró que se puede tomar C = 1/(8 π) para todo x ≥ 2657.
Los ceros de la función zeta y los números primos satisfacen ciertas propiedades de dualidad, conocidas como fórmulas explícitas, que muestran, usando análisis de Fourier, que los ceros de la función zeta de Riemann pueden interpretarse como frecuencias armónicas en la distribución de los números primos.
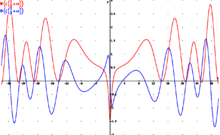
Más aún, si la conjetura de Hilbert-Polya es cierta, entonces cualquier operador que nos dé las partes imaginarias de los ceros como sus valores propios debe satisfacer:
donde tr es la traza del operador (suma de sus valores propios),  es un número imaginario y
es un número imaginario y  es la función de Chebyshov que nos suma el log(x) sobre los primos y sus potencias enteras, dicha fórmula es una conclusión de la ‘fórmula explicita’ de V. Mangoldt.5 Varios operadores propuestos por C. Perelman, J. Macheca y J. García, parecen corroborar los resultados de la conjetura de Hilbert sobre el operador, reproduciendo la parte imaginaria de los ceros.
es la función de Chebyshov que nos suma el log(x) sobre los primos y sus potencias enteras, dicha fórmula es una conclusión de la ‘fórmula explicita’ de V. Mangoldt.5 Varios operadores propuestos por C. Perelman, J. Macheca y J. García, parecen corroborar los resultados de la conjetura de Hilbert sobre el operador, reproduciendo la parte imaginaria de los ceros.
Cálculo numérico
- En el año 2004 Xavier Gourdon verificó la conjetura de Riemann numéricamente a lo largo de los primeros diez trillones de ceros no triviales de la función. Sin embargo esto no es estrictamente una demostración, numéricamente es más interesante encontrar un contraejemplo, es decir un valor de cero que no cumpla con que su parte real es 1/2, pues esto echaría por los suelos la validez de la conjetura.
- Hasta el 2005, el intento más serio para explorar los ceros de la función-ζ, es el ZetaGrid, un proyecto de computación distribuida con la capacidad de verificar billones de ceros por día. El proyecto acabó en diciembre de 2005, y ninguno de los ceros pudo ser identificado como contraejemplo de la hipótesis de Riemann.
Referencias
- Bombieri, Enrico (2000) (en inglés, PDF), The Riemann Hypothesis – official problem description, Clay Mathematics Institute, consultado el 21 de febrero de 2011 Reimpreso en (Borwein et al., 2008).
- «The Millennium Prize Problems» (en inglés). Consultado el 21 de febrero de 2011.
- http://www.hrpub.org/journals/jou_info.php?id=26 Vol 1 (2) 2013
- Riemann, Bertrand (1859). «Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse». Consultado el 29 de diciembre de 2008.
- Explicit formula http://www.wbabin.net/science/moreta8.pdf
Fuente: Wikipedia, 2015.
.
.
Números primos, claves y grandes números
abril 6, 2014
Primos, claves y grandes números
Extraído de Selección de textos divulgativos, Ed. Anaya. Vol. IV.
Todos utilizamos claves secretas. Si encendemos el teléfono móvil, nos pide un PIN. Para acceder al correo electrónico, utilizamos una contraseña. Al sacar dinero del cajero automático con una tarjeta, necesitamos teclear un número personal.
Normalmente, las claves no se las comunicamos a nadie que no sea de absoluta confianza. Los bancos toman grandes precauciones cuando envían números secretos a sus clientes; si quieres comprobar cuáles son, no tienes más que preguntar. ¿Imaginas qué ocurriría si la gente tuviera la clave privada de las cuentas del supermillonario Bill Gates, por ejemplo?
Después de los bancos, quienes guardan más secretos son los militares y los espías. Hace dos mil años, cuando Julio César enviaba mensajes a sus generales lo hacía utilizando un código cifrado que había copiado de los egipcios, basado en cambiar unas letras por otras, siguiendo una regla de sustitución que variaba con cada mensaje. Aunque el sistema era bastante primitivo, casi un juego, resultaba eficaz, entre otras cosas, porque entonces no había mucha gente que supiera leer y escribir.
En este código de sustitución, el mensaje «NECESITAMOS REFUERZOS» se convertía, por ejemplo, en «FWUWLAMSEHLSKWXNWKRHL», desplazando ocho lugares a la izquierda la posición de las letras y utilizando la letra S como espacio, para complicar un poco las cosas. Quien recibía ‘el mensaje debía conocer la clave, que podía variar cada poco tiempo.
Con el tiempo, los códigos se hicieron cada vez más complicados y descifrar mensajes secretos comenzó a requerir mucho tiempo y trabajo. A partir del siglo XV, muchos científicos y nobles se entretenían en enviarse mensajes codificados, por el simple capricho de desafiar a los contrincantes. A veces se añadían tintas invisibles, diagramas o dibujos simbólicos, a los que se asignaba un papel especial. Eran tiempos en los que se buscaba la piedra filosofal, que convertiría en oro cualquier metal, y por toda Europa circulaban documentos que solo los expertos en esos símbolos sabían descifrar.
Pero los mensajes secretos más secretos eran los de los militares y los espías. Desde aquella época, raro era el ejército que no contara con encargados que codificaran y descodificaran mensajes, inventando claves cada vez más complejas. Muchos correos, a pie, a caballo o en barco, eran perseguidos para interceptar sus cartas en clave. Algunas tardaron años en descifrarse, y en siglo XIX el escritor Edgar Alan Poe, un experto en criptografía, consideraba que nunca podría escribirse un mensaje que no fuera descifrado por otro ser humano.
La llegada del teléfono y de la radio supuso una ventaja para los espías, pero también para los contraespías. Los primeros podían enviar mensajes secretos a gran distancia e instantáneamente, pero era difícil impedir que los segundos intervinieran la línea u oyesen la radio. Además, quien enviaba los mensajes nunca sabía si el mensaje había sido interceptado.
Eso llevó a buscar códigos y sistemas de cifrado cada vez más complicados, que se hicieron monstruosos. Durante la Primera Guerra Mundial, entre 1914 y 1918, los alemanes manejaban un diccionario de claves que tenía cerca de treinta y cinco mil palabras y reglas distintas. Incluso cuando se conocían las claves, descifrar un mensaje era una tarea muy costosa. Dependiendo del día, de la hora o de ciertas características especiales, como si el número de caracteres era o no múltiplo de cinco, una frase como «LAS GAVIOTAS VUELAN MUY ALTO» se podía convertir en «MAÑANA ATACAREMOS DESPUÉS DEL BOCADILLO» o «SE HAN ESTROPEADO LOS CAÑONES».
Como siempre, llegan las máquinas
Poco antes del comienzo de la Segunda Guerra Mundial, los alemanes construyeron una máquina de escribir especial, a la que llamaron Enigma, que convertía un mensaje cualquiera en un código secreto mediante un dispositivo electrónico.
Las claves eran tan variadas y cambiantes que solo había una posibilidad entre muchos trillones de adivinada por casualidad. Comenzó entonces una verdadera batalla en las sombras. Por un lado, los espías ingleses intentaron robar una Enigma. Por otro, los militares pidieron ayuda a los científicos para construir máquinas capaces de descodificar mensajes realizando cálculos y combinaciones miles de veces más rápido que cualquier ser humano. Así es como surgió uno de los primeros ordenadores, llamado Colossus.
Con ayuda de máquinas o sin ellas, descodificar mensajes cifrados fue fundamental para inclinar las batallas hacia uno u otro bando. Los japoneses, por ejemplo, utilizaron un sistema con cuarenta y cinco mil números de cinco cifras, cada uno de los cuales codificaba una palabra, una letra o una frase. A pesar de su dificultad, estos mensajes fueron descifrados por los primeros ordenadores; era una cuestión de potencia y rapidez de cálculo. Gracias a eso, los estadounidenses se anticiparon a uno de los ataques japoneses, lo que decidió el curso de la guerra.
Desde esa época comenzó una guerra sorda entre los espías, diplomáticos y militares, cada vez con ordenadores más potentes y rápidos. Si un bando disponía de una máquina capaz de generar claves complicadas, el otro trataba de hacerse con otra más potente capaz de descifradas. La cuestión que todos los científicos se preguntaban era: ¿Existirá algún procedimiento para codificar un mensaje que no pueda ser descifrado por ninguna máquina, por poderosa que sea, al cabo de un tiempo razonable? (Digamos, ¿mil años?).
Antes de responder esta pregunta, es interesante contar una anécdota para saber cómo funcionan las claves secretas.
Mensajes indios
También durante la Segunda Guerra Mundial, a alguien se le ocurrió una idea genial: pedir ayuda a los indios dakota para codificar mensajes secretos. El asunto era sencillo. Alguien dictaba a un indio dakota una orden como, por ejemplo, «MAÑANA LLEGA EL BARCO CON PROVISIONES». El indio la traducía a su idioma y la dictaba por teléfono. Pongamos por caso, se leía como «DAQ-LABA’NAATAN-DULUQ-CHEETAQ». Al otro lado del teléfono había otro indio dakota que escuchaba el mensaje y lo volvía a traducir al idioma original.
¡Era asombrosamente simple! Ya no importaba que el enemigo escuchara los mensajes, porque solo un indio dakota podía descifrados. La ventaja del lenguaje dakota era triple: solo había indios dakota en Estados Unidos, era un idioma que nunca se había escrito y solo lo conocían los dakota. Esto es lo que se llama un mensaje público: no importa que lo oiga la gente porque casi nadie lo entendería.
Secuestrar a un indio dakota se convirtió para el ejército japonés en algo tan obsesivo como para los ingleses robar una Enigma, porque solo un dakota podía entender ese mensaje público. Curiosamente, gracias a los códigos cifrados esos soldados indios se convirtieron en personas valiosísimas en Estados Unidos, cuando siempre habían estado marginados. Hay una película, llamada Windtalkers, que cuenta precisamente la historia de uno de estos indios.
A través de los indios dakota se comprendió que el meollo del secreto de un mensaje secreto no está en que se intercepte, sino en que no haya nadie (¡ni nada!, ¡ni siquiera una maquinal) que pueda descifrado, a no ser que se conozca la clave. Y aquí es donde volvemos a la pregunta: ¿Es posible codificar un mensaje público que no sea descifrado ni siquiera por un ordenador potente, al cabo de mil años de cálculos super rápidos?
Aquí intervienen las matemáticas
Estamos tan acostumbrados a los números que muchas veces no nos detenemos a pensar en las posibilidades que encierran.
Si diez personas deciden sentarse en un banco del parque con todas las combinaciones posibles, el número de formas distintas en que pueden hacerlo es de 3 628 800. Si lograran hacer un cambio por segundo, sin dormir, comer ni parar por ningún motivo, eso les llevaría nada menos que cuarenta y dos días.
Si en lugar de ser diez, son veinte personas, y deciden hacer todas las combinaciones posibles, llegarán al pasmoso número 2432902008176640000, que los matemáticos leen en notación científica como 2,4.1018 y que los mortales llamamos, sencillamente, «dos trillones y medio». Para que esas veinte personas consigan sentarse de todas las formas posibles, a razón de un cambio por segundo, necesitaríamos 77 146 816 596 años. O sea, ¡unas dieciocho veces la edad que tiene el planeta Tierra!
Si el número de personas asciende a 100, el número de combinaciones posible asciende a 9,33.10157 y el número de años sube a 2,96 1015. Realmente, en este punto hemos perdido toda capacidad de imaginación. No hay nada en el universo, ni siquiera electrones suficientes, que justifique utilizar ese número en algo contable…
A partir de 1015, los matemáticos consideran que ese número es «grande». Es cierto que los superordenadores actuales son realmente potentes y que pueden realizar trillones de operaciones por segundo. Pero aunque una máquina fuera capaz de efectuar sextillones de cálculos por segundo, aun trabajando durante miles de años, no podría encontrar algo que está bien escondido. La clave está en ocultarlo bien.
Las primeras claves numéricas
Si alguien codificara letra a letra El Quijote, siguiendo un sistema como el utilizado por Julio César, descifrado sería un juego largo e incómodo, pero sencillo. También lo sería si sustituyera cada letra por un cierto número. Todos los códigos de sustitución y desplazamiento son fáciles de destripar con solo hacer un análisis estadístico de letras. En español, la E es la que aparece más veces, seguida de la A, por ejemplo.
El asunto se complica si sustituimos y ocultamos siguiendo una clave y una operación. Por ejemplo, la frase «En un lugar… » se puede sustituir por «112028201828133425». Hasta aquí, se ha hecho una simple sustitución, fácil de descubrir. Pero si esa serie se divide en grupos de nueve (11202820828133425) y después se le suma una clave secreta (pongamos por caso 740321821896110942), eliminando la primera cifra de cada grupo si al sumar se obtienen más de nueve cifras, se obtiene el mensaje 852350022724244367.
Aquí ya no hay regla estadística que valga. Si se conoce la clave, lo que hay que hacer para restaurar el mensaje original es primero restar y luego descodificar. Pero si no se conoce la clave, descifrar el mensaje es un quebradero de cabeza. En esta doble operación de sustituir y operar se basaban muchos códigos secretos de la época en que no había ordenadores.
Sin embargo, para un ordenador descifrar este mensaje resulta una tarea relativamente sencilla. Es cuestión de probar miles de millones de combinaciones y aplicar reglas estadísticas, y una máquina suma y multiplica cifras a una velocidad pasmosa, con lo que, al final, destripa cualquier mensaje de este tipo.
Cuando se pidió ayuda a los matemáticos, estos pensaron en una tarea difícil incluso para un ordenador. E inmediatamente recurrieron a los números primos.
La dificultad de los grandes primos
Como es sabido, un número primo es aquel que no tiene más divisores que sí mismo y la unidad. Para saber si un número es o no primo (y son candidatos teóricos los que no acaban en 0, cifra par o 5), un procedimiento eficaz consiste en probar a dividido por todos los números enteros que sean impares y menores que su raíz cuadrada. Para 2011, por ejemplo, habrá que hacer 21 tanteos; al no encontrar ningún divisor, diremos que 2011 es primo.
Hacer 21 divisiones y comprobaciones es muy simple para un ordenador. Tarda apenas un microsegundo. El asunto lo complicamos un poco si queremos comprobar si el número 2467043539 es o no primo, porque habría que hacer 24834 divisiones. Con un número de diecisiete dígitos, el número de divisiones asciende a 150 millones. Y si el número tiene cien cifras, los ensayos son ya 1050. Todavía no entramos en el territorio de los números grandes, pero falta poco…
Con números de 128 o de 256 cifras, el asunto se complicará enormemente. (En realidad, las cosas no son del todo así. Es mucho más sencillo saber si un número es primo que calcular cuáles son sus divisores, porque los matemáticos han desarrollado procedimientos muy poderosos que no viene a cuento describir aquí). Con esos métodos, saber si un número impar de 200 cifras es primo (en caso de que lo sea) requiere varios minutos de tiempo en su superordenador. Pero determinar cuáles son sus dos divisores de 100 cifras requeriría en esa misma máquina ¡varios millones de años de funcionamiento!
A secretos colosales, números colosales
En 1977, el célebre divulgador matemático Martin Gardner propuso un problema que hoy es famoso: encontrar los factores de un número primo de 129 cifras y, con ello, descifrar un mensaje oculto en una clave. Consideraba entonces altamente improbable que alguien lograra factorizar ese número con los métodos de trabajo existentes en la época. Pero diecisiete años más tarde, utilizando la potencia de cálculo de cientos de ordenadores trabajando conjuntamente a través de internet, se logró encontrar sus divisores y descifrar el mensaje original, que tenía cuarenta letras.
Para mayor seguridad, hoy en día las “claves de encriptación” de documentos muy secretos maneja números primos de 230 cifras. Estos números son públicos; es decir, cualquiera (casi cualquiera, podríamos decir) puede utilizarlos para enviar mensajes, pero solo quienes conozcan sus factores pueden descifrarlos. Y se confía en que esos factores no sean calculados ni descubiertos en un plazo de tiempo prudencial.
El código pin de nuestro teléfono móvil suele constar de cuatro cifras; si lo perdemos y alguien intenta ponerlo en funcionamiento, dispone de tres intentos. En caso de no acertar con el pin, el teléfono se bloquea y para reactivado se necesita un código puk que ya tiene ocho dígitos. Es una muy buena medida de seguridad; a menos que nos roben el puk, desbloquear el teléfono resulta casi imposible para un profano.
Pero nuestro teléfono móvil es un pequeño secreto. Las cuentas de nuestro banco están protegidas con códigos de seguridad que son mucho más difíciles de descifrar, porque constituyen un secreto algo mayor. Y los datos o noticias que circulan entre poderosas corporaciones económicas y militares son verdaderamente secretos y sus usuarios consideran que deben ser indescifrables. No es extraño que estén codificados con números de más de doscientas cifras.
Actualmente, con al auge del correo electrónico y de Internet, hay dos rasgos que tienen que ver con el cifrado de datos: la autenticidad y la ocultación.
La autenticidad trata de garantizar que la persona que remite un documento es quien realmente dice ser. Durante siglos, esto se ha conseguido mediante la firma autógrafa; es decir, el conjunto de garabatos escritos con el que nos identificamos al firmar.
Cuando hace años se popularizó el uso del DNI, con un número, cualquiera podía inventarse al instante uno como, por ejemplo, 3602466. Posteriormente, se añadió una letra de control para garantizar que ese número fuese válido, y así se creó el NIF. Esa letra añadida se obtiene haciendo la división entera del DNI entre 23, tomando el resto y asignando a ese resto una letra siguiendo cierto criterio: A=3, B= 11, C=20, D=9, etc. En principio, podría pensarse que cualquiera que sepa dividir y conozca la tabla de asignación podría inventarse un NIF, con un número y su correspondiente letra.
Como el NIF no sirve para identificar a una persona, ya se han puesto en marcha procedimientos para garantizar la autenticidad de los firmantes, sobre todo si operan a través de Internet. Es el caso de la firma electrónica, un código de caracteres generado por procedimientos matemáticos en los que intervienen números primos larguísimos, casi imposibles de factorizar. Es muy probable que, dentro de unos años, tus documentos electrónicos aparezcan firmados con una ristra de letras y números similar a 8026565789035dc927a7428cd1360572fe…, y así hasta 166 caracteres.
El segundo aspecto, el de la ocultación, es el que se refiere al cifrado del contenido de los mensajes. Como es fácil de suponer, disponer de un código secreto indescifrable solo está al alcance de quienes tienen secretos que guardar y disponen de ordenadores muy potentes.
Para acabar, ¿vale tanto un secreto?
Por encima de nuestras cabezas, a la velocidad de la luz, cabalgando por satélites, cables y antenas, viajan billones de datos cifrados que contienen secretos económicos, científicos y militares. Son codificados y descodificados por potentes ordenadores, que operan con números primos titánicos’. Estas máquinas son manejadas por hombres y mujeres muy inteligentes, a veces geniales, que han dedicado parte de sus vidas a esconder una información que consideran muy valiosa, para que otros hombres y mujeres, también geniales, no puedan descifrada en sus vidas, aunque dediquen su existencia a ello.
Desde cierto punto de vista, resulta asombroso que haya seres humanos capaces de plantear problemas que otros humanos no puedan resolver jamás, ni siquiera con ayuda de superordenadores.
Desde otro punto de vista, quizá resulte absurdo. Mientras se construyen mensajes que se consideran invulnerables, estamos indefensos ante el ataque de un virus. Por otra parte, esta batalla resulta tan antigua como la de la espada contra el escudo.
Al escribir estas líneas se tienen noticias de que el número primo más grande conocido hasta la fecha es el 230402457-1, que convierte en liliputienses los números grandes de los que hemos hablado antes y que ha sido obtenido, naturalmente, con ayuda de una máquina. Por otro lado, se habla ya de los futuros ordenadores cuánticos, que aseguran serán capaces de resolver en pocas horas tareas que los superordenadores actuales tardarían miles de años en llevar a cabo.
¿Se podrá descifrar en algún momento un mensaje que en otro momento se considere indescifrable? Quizá la respuesta sea, como diría Julio César si supiera multiplicar, 52443644 2252 7256225254304440 7422 543022384644.
El asunto está en si tanto secreto merece, de verdad, tanto esfuerzo.
– – – – – – – – –
—————————————-
Cambie sus claves periódicamente
La primera medida de seguridad en Internet (y en todo medio electrónico) es la Clave, en otros sitios conocida como el PIN (personal Identificatión Number) o número de identificación personal. Sin embargo, la mayoría de las personas no cambia su clave nunca.
Fórmese el hábito de cambiar su clave con periodicidad. En algunos servicios le «obligan» a cambiar la clave cada cierto tiempo, por lo general en forma semestral. Sin embargo es indispensable que usted forme el hábito de cambiar su clave por lo menos una ves al mes, la de todos sus servicios: bancaria, acceso a Internet, correo, etc.
Use una combinación de letras y números, y tenga en cuenta que en algunos servicios se reconocen y distinguen las mayúsculas de las minúsculas. Si puede, haga uso de caracteres especiales también, como los signos de más y menos.
En el caso de los Pines bancarios, que solo son números, se recomienda cambiarla con mayor frecuencia.
Fuente: DeltaAsesores.com




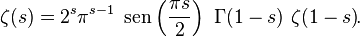

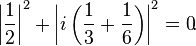


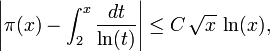
![\sum_{n}e^{-\beta E_{n}}=\operatorname{tr}[e^{-\beta \hat H}]=e^{u/2}-e^{-u/2} \frac{d\psi _{0}}{du}-\frac{e^{u/2}}{e^{3u}-e^{u}},](https://upload.wikimedia.org/math/e/d/6/ed6dc5f5af88bc8ded7ea7ede290923a.png)