La hipótesis de Riemann, ¿resuelta?
noviembre 18, 2015 · Imprimir este artículo
Un profesor asegura haber resuelto un problema matemático de 156 años
La hipótesis de Riemann. El nigeriano Opeyemi Enoch afirma haber llegado al resultado. Trabajó durante cinco años en el problema. Pero llevara varios años determinar si efectivamente lo resolvió. De ser correcto, se ganará un premio de un millón de dólares.

El profesor nigenirano Opeyemi Enoch, quien habría resuelto el problema matermático de la hipótesis de Riemann.
Un profesor nigeriano asegura haber resuelto uno de los problemas matemáticos del siglo y podría hacerse acreedor de un premio de un millón de dólares. Se trata de la hipótesis de Riemann, que fue planteada por primera vez en 1859 por el académico Bernhard Riemann, y forma parte de uno de los siete problemas matemáticos del milenio.
Ahora, el Instituto Clay de Matemáticas deberá determinar si el resultado es el correcto y, de ser así, le otorgaría el premio de un millón de dólares al profesor Opeyemi Enoch.
Según cuenta el profesor, a lo largo de estos cinco años hubo dos momentos clave, en los que intuyó que estaba cerca del resultado. «Uno fue en una mañana de 2010, cuando di con el vínculo del problema. Ahí supe que me estaba acercando mucho», cuenta. Luego, continúa, encontró la forma de aplicar lo que había descubierto hasta entonces.
Ahora, el Instituto Clay debe revisar el trabajo de Enoch y dictar un «veredicto». Sin embargo, eso llevará su tiempo. En las reglas que publica el Instituto Clay para dar por resuelto el problema y otorgar el premio, se encuentran las siguientes condiciones: la solución debe haber sido publicada por alguna revista de reputación mundial; la solución debe tener aceptación por parte de la comunidad matemática dos años después. Y recién pasados esos dos años, el instituto tomará una decisión.
La hipótesis de Riemann es uno de los siete problemas matemáticos del milenio. De esos siete problemas ya fue resuelto uno. El de Riemann sería el segundo. Y aún quedan por resolver otros cinco problemas.
Fuente: clarin.com, 18/11/15.
Ver una opinión en contrario:
La supuesta demostración del nigeriano Enoch de la hipótesis de Riemann
Vincúlese a nuestras Redes Sociales:
Google+ LinkedIn YouTube Facebook Twitter
Hipótesis de Riemann
 En matemática pura, la hipótesis de Riemann, formulada por primera vez por Bernhard Riemann en 1859, es una conjetura sobre la distribución de los ceros de la función dseta de Riemann ζ(s).1
En matemática pura, la hipótesis de Riemann, formulada por primera vez por Bernhard Riemann en 1859, es una conjetura sobre la distribución de los ceros de la función dseta de Riemann ζ(s).1
La hipótesis de Riemann, por su relación con la distribución de los números primos en el conjunto de los naturales, es uno de los problemas abiertos más importantes en la matemática contemporánea.
El Instituto Clay de Matemáticas ha ofrecido un premio de un millón de dólares a la primera persona que desarrolle una demostración correcta de la conjetura.2 La mayor parte de la comunidad matemática piensa que la conjetura es correcta, aunque otros grandes matemáticos como J. E. Littlewood y Atle Selberg se han mostrado escépticos, si bien el escepticismo de Selberg fue disminuyendo desde sus días de juventud. En un artículo en 1989 sugirió que un análogo debe ser cierto para una clase mucho más amplia de funciones (la clase de Selberg).
El profesor nigeriano Opeyemi Enoch, quien trabaja en la Universidad Federal de Oye Ekiti en Nigeria, aparentemente ha resuelto el problema de Riemann; el instituto Clay debe hacer la revisión respectiva para confirmar la solución propuesta, según despacho de BBC Mundo del 17 de Noviembre de 2.015: «El profesor que asegura haber resuelto un problema matemático de más de 150 años»..
Definición
La función dseta de Riemann ζ(s) está definida de la siguiente manera:
Para todos los números complejos s ≠ 1, se puede prolongar analíticamente mediante la ecuación funcional:
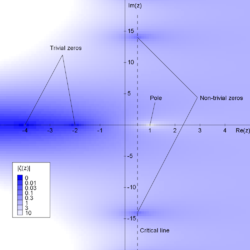
Esta posee ciertos valores, llamados ceros «triviales» para los cuales la función zeta se anula. De la ecuación se puede ver que s = −2, s = −4, s = −6, … son ceros triviales. Existen otros valores complejos s comprendidos entre 0 < Re(s) < 1, para los cuales la función zeta también se anula, llamados ceros «no triviales». La conjetura de Riemann hace referencia a estos ceros no triviales afirmando:
|
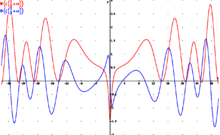
Por lo tanto los ceros no triviales deberían encontrarse en la línea crítica s = 1/2 + i t donde t es un número real e i es la unidad imaginaria. La función zeta de Riemann, a lo largo de la línea crítica ha sido estudiada en términos de la función Z, cuyos ceros corresponden a los ceros de la función zeta sobre la línea crítica.
Recordemos lo que en su memoria Riemann afirma.
1º- :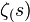 tiene infinitos ceros complejos que estan en la linea recta. Re
tiene infinitos ceros complejos que estan en la linea recta. Re 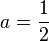
y lm s = 0.
2º- Es muy probable que la raiz de una función x son reales.
Es decir  ; (
; (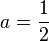 ;
; 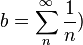 .
.
Esto lo ha demostrado la matemática Albana Diez3 para: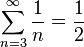
:
Indico una de las series para 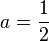 ; no solo existen para este valor, tambien para
; no solo existen para este valor, tambien para 
Historia
Riemann mencionó la conjetura en 1859, que sería llamada la hipótesis de Riemann, en su tesis de doctorado Sobre los números primos menores que una magnitud dada, al desarrollar una fórmula explícita para calcular la cantidad de primos menores que x. Puesto que no era esencial para el propósito central de su artículo, no intentó dar una demostración de la misma. Riemann sabía que los ceros no triviales de la función zeta están distribuidos en torno a la recta s = 1/2 + i t, y sabía también que todos los ceros no triviales debían estar en el rango 0 ≤ Re(s) ≤ 1.4
En 1896, Hadamard y de la Vallée-Poussin probaron independientemente, que ningún cero podía estar sobre la recta Re(s) = 1. Junto con las otras propiedades de los ceros no triviales demostradas por Riemann, esto mostró que todos los ceros no triviales deben estar en el interior de la banda crítica 0 < Re(s) < 1. Este fue un paso fundamental para las primeras demostraciones del teorema de los números primos.
En 1900, Hilbert incluyó la hipótesis de Riemann en su famosa lista de los 23 problemas no resueltos — es parte del problema 8 en la lista de Hilbert junto con la conjetura de Goldbach. Cuando se le preguntó qué haría si se despertara habiendo dormido quinientos años, remarcablemente Hilbert contestó que su primera pregunta sería si la hipótesis de Riemann había sido probada. La hipótesis de Riemann es el único problema de los que propuso Hilbert que está en el premio del milenio del Instituto Clay de Matemáticas.
En 1914, Hardy demostró que existe un número infinito de ceros sobre la recta crítica Re(s) = 1/2. Sin embargo todavía era posible que un número infinito (y posiblemente la mayoría) de los ceros no triviales se encontraran en algún otro lugar sobre la banda crítica. En trabajos posteriores de Hardy y Littlewood en 1921 y de Selberg en 1942 se dieron estimaciones para la densidad promedio de los ceros sobre la línea crítica.
Trabajos recientes se han concentrado en el cálculo explícito de la localización de grandes cantidades de ceros (con la esperanza de hallar algún contraejemplo) y en el establecimiento de cotas superiores en la proporción de ceros que puedan estar lejos de la línea crítica (con la esperanza de reducirlas a cero).
La hipótesis de Riemann y los números primos
La formulación tradicional de la hipótesis de Riemann oscurece un poco la importancia real de la conjetura. La función zeta de Riemann tiene una profunda conexión con los números primos y Hege von Koch demostró en 1901 que la hipótesis de Riemann es equivalente al considerable refinamiento del teorema de los números primos: Existe una constante C > 0 tal que
para todo x suficientemente grande, donde π(x) es la función contadora de primos y ln(x) es el logaritmo natural de x. Lowell Schoenfeld mostró que se puede tomar C = 1/(8 π) para todo x ≥ 2657.
Los ceros de la función zeta y los números primos satisfacen ciertas propiedades de dualidad, conocidas como fórmulas explícitas, que muestran, usando análisis de Fourier, que los ceros de la función zeta de Riemann pueden interpretarse como frecuencias armónicas en la distribución de los números primos.
Más aún, si la conjetura de Hilbert-Polya es cierta, entonces cualquier operador que nos dé las partes imaginarias de los ceros como sus valores propios debe satisfacer:
donde tr es la traza del operador (suma de sus valores propios),  es un número imaginario y
es un número imaginario y  es la función de Chebyshov que nos suma el log(x) sobre los primos y sus potencias enteras, dicha fórmula es una conclusión de la ‘fórmula explicita’ de V. Mangoldt.5 Varios operadores propuestos por C. Perelman, J. Macheca y J. García, parecen corroborar los resultados de la conjetura de Hilbert sobre el operador, reproduciendo la parte imaginaria de los ceros.
es la función de Chebyshov que nos suma el log(x) sobre los primos y sus potencias enteras, dicha fórmula es una conclusión de la ‘fórmula explicita’ de V. Mangoldt.5 Varios operadores propuestos por C. Perelman, J. Macheca y J. García, parecen corroborar los resultados de la conjetura de Hilbert sobre el operador, reproduciendo la parte imaginaria de los ceros.
Cálculo numérico
- En el año 2004 Xavier Gourdon verificó la conjetura de Riemann numéricamente a lo largo de los primeros diez trillones de ceros no triviales de la función. Sin embargo esto no es estrictamente una demostración, numéricamente es más interesante encontrar un contraejemplo, es decir un valor de cero que no cumpla con que su parte real es 1/2, pues esto echaría por los suelos la validez de la conjetura.
- Hasta el 2005, el intento más serio para explorar los ceros de la función-ζ, es el ZetaGrid, un proyecto de computación distribuida con la capacidad de verificar billones de ceros por día. El proyecto acabó en diciembre de 2005, y ninguno de los ceros pudo ser identificado como contraejemplo de la hipótesis de Riemann.
Referencias
- Bombieri, Enrico (2000) (en inglés, PDF), The Riemann Hypothesis – official problem description, Clay Mathematics Institute, consultado el 21 de febrero de 2011 Reimpreso en (Borwein et al., 2008).
- «The Millennium Prize Problems» (en inglés). Consultado el 21 de febrero de 2011.
- http://www.hrpub.org/journals/jou_info.php?id=26 Vol 1 (2) 2013
- Riemann, Bertrand (1859). «Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse». Consultado el 29 de diciembre de 2008.
- Explicit formula http://www.wbabin.net/science/moreta8.pdf
Fuente: Wikipedia, 2015.
.
.




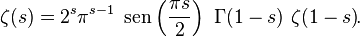

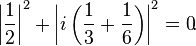


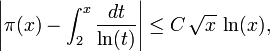
![\sum_{n}e^{-\beta E_{n}}=\operatorname{tr}[e^{-\beta \hat H}]=e^{u/2}-e^{-u/2} \frac{d\psi _{0}}{du}-\frac{e^{u/2}}{e^{3u}-e^{u}},](https://upload.wikimedia.org/math/e/d/6/ed6dc5f5af88bc8ded7ea7ede290923a.png)

[…] La hipótesis de Riemann, ¿resuelta? […]
[…] La hipótesis de Riemann, ¿resuelta? […]