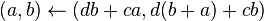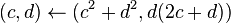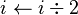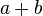El Encanto Matemático: Un viaje revelador a través de Fibonacci y Zeckendorf
mayo 16, 2024
Por Gustavo Ibáñez Padilla.
En el complejo y misterioso mundo de las matemáticas, hay ciertos fenómenos que capturan en forma inmediata la imaginación del público en general. Uno de esos enigmas fascinantes es la relación entre la Sucesión de Fibonacci y el Teorema de Zeckendorf. ¿Qué tienen en común estas dos joyas matemáticas? ¿Y por qué nos siguen sorprendiendo hasta el día de hoy? Lo veremos a continuación.
La sucesión de Fibonacci es, sin duda, una de las secuencias más famosas en el mundo de las matemáticas. Comienza con los números 0 y 1, y cada número subsiguiente es la suma de los dos anteriores. Así, la secuencia resulta ser: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, y así sucesivamente hasta el infinito. Esta secuencia aparentemente simple ha fascinado a matemáticos, artistas e incluso biólogos debido a su aparición en una enorme variedad de fenómenos naturales, desde la disposición de las hojas en una rama hasta los patrones de crecimiento de los girasoles.
La historia de la sucesión de Fibonacci se remonta al siglo XIII, a un hombre conocido como Leonardo de Pisa, comúnmente llamado Fibonacci. En su influyente libro Liber Abaci, publicado en 1202, Fibonacci presentó al mundo occidental los números indo-arábigos y sus aplicaciones en la aritmética. Pero lo que llamó la atención de muchos fue un problema aparentemente simple sobre el crecimiento de una población de conejos, que llevó al descubrimiento de la secuencia de números que ahora lleva su nombre.
¿Cuál es la relación de Fibonacci con el teorema de Zeckendorf? Pues que este teorema afirma que: Todo entero positivo se escribe, de manera única, como suma de números de Fibonacci no consecutivos. A esa escritura única se le llama la descomposición de Zeckendorf del número en cuestión.
Así pues, todos los números naturales pueden expresarse como la suma de números de Fibonacci únicos. Es decir, cada número natural puede descomponerse de manera única como una suma de números de Fibonacci, sin que ninguno de ellos se repita. Esta descomposición única es lo que hace que el teorema de Zeckendorf sea tan intrigante, ya que revela una estructura ordenada y predecible que ha fascinado a generaciones de matemáticos. ( Por ejemplo: 10= 2+8 ; 26 = 5+21 ; 43 = 1+8+34 )
El matemático francés Édouard Lucas, famoso por su trabajo en Teoría de números y sus libros de matemáticas recreativas, manifestó: “Los números de Fibonacci son como un gran cuento, lleno de sorpresas y misterios, esperando ser descubiertos”. Fue Lucas quien le puso el nombre a esta famosa sucesión, de la cual descubrió numerosas características, desde patrones geométricos hasta propiedades únicas en teoría de números.
Una de las sorpresas más asombrosas de este universo matemático es la relación entre la sucesión de Fibonacci y la proporción áurea representada por el número φ (phi), cuyo valor es aproximadamente igual a 1,618, un número misterioso que parece resonar en los rincones más profundos de la naturaleza y el arte. Como si estuvieran bailando al unísono, los números de Fibonacci revelan una conexión íntima con esta proporción divina a medida que crecen hacia el infinito, como si estuvieran siguiendo una partitura escrita en el corazón mismo de la realidad.
“Las matemáticas son la poesía del universo”, sostuvo el genial matemático David Hilbert, y en la intersección de Fibonacci y Zeckendorf, encontramos una poesía matemática que cautiva y encanta con su elegancia y misterio.
Estas sorprendentes relaciones e intersecciones entre diversos conceptos matemáticos son las que nos llevan a afirmar que las matemáticas son una verdadera unidad, lo cual llevo también a los ’modernos’ a denominarla en singular y con mayúscula, como Matemática.
“Los números de Fibonacci son como una sinfonía matemática, cada uno tocando su propia melodía única, pero juntos creando una armonía incomparable” afirmaba Lucas. ¿Qué papel desempeña el teorema de Zeckendorf en esta sinfonía matemática? Resulta que este teorema proporciona un marco ordenado y estructurado para entender cómo los números naturales se descomponen en términos de números de Fibonacci únicos. Es como si cada número natural tuviera una historia que contar, una historia que se revela a través de su descomposición en términos de esta antigua secuencia numérica.
“Las matemáticas son el arte de dar el mismo nombre a diferentes cosas”, dijo el matemático francés Henri Poincaré, y resulta evidente en la intersección de Fibonacci y Zeckendorf. A través de estas ideas aparentemente abstractas, descubrimos un mundo rico y vibrante de posibilidades matemáticas que nos desafían a mirar más allá de la superficie y explorar las profundidades del universo numérico.
Pero la diversión matemática no se detiene aquí. El teorema de Zeckendorf ha inspirado una serie de acertijos y juegos matemáticos que desafían la mente y estimulan el pensamiento creativo. Desde rompecabezas de descomposición de números hasta juegos de estrategia basados en la sucesión de Fibonacci, hay un mundo de aventuras matemáticas esperando ser exploradas por aquellos dispuestos a sumergirse en sus misterios.
Y no debemos olvidar el encanto de la matemagia, un arte que combina ilusionismo y matemáticas para crear asombrosos trucos de números y acertijos. Maestros de la matemagia como Sam Lloyd y Henry Dudeney han seducido audiencias con sus trucos ingeniosos basados en principios matemáticos, recordándonos que las matemáticas pueden ser tanto sorprendentes como entretenidas, como bien lo explica Martin Gardner en su libro Matematica, magia y misterio.
La Sucesión de Fibonacci y el Teorema de Zeckendorf nos invitan a un viaje fascinante a través del rico y sorprendente mundo de las matemáticas. Desde su aparición en la naturaleza hasta su aplicación en la teoría de números y los juegos matemáticos, estas ideas continúan maravillando y deleitando a quienes se aventuran en el emocionante viaje de descubrimiento matemático.
En palabras del prolífico matemático Paul Erdős: “Las matemáticas son como una aventura sin fin, siempre hay nuevas maravillas por descubrir”. Y en el universo de las matemáticas recreativas Fibonacci, Zeckendorf y sus seguidores están siempre listos para sorprender y extasiar a aquellos que se atreven a adentrarse en sus misterios.
Fuente: Ediciones EP, 16/05/24.
Información sobre Gustavo Ibáñez Padilla
Este artículo también ha sido publicado en Mendoza Today

Más información:
Los números en la naturaleza
Matemáticas: ¿descubrimiento o creación?
La importancia del Azar: Más allá de un juego de dados
.
.
Los números en la naturaleza
septiembre 30, 2018
La sucesión de Fibonacci en la naturaleza
Sucesión de Fibonacci
En matemáticas, la sucesión de Fibonacci (a veces mal llamada serie de Fibonacci) es la siguiente sucesión infinita de números naturales:
La sucesión comienza con los números 1 y 1,1 y a partir de estos, «cada término es la suma de los dos anteriores», es la relación de recurrencia que la define.
A los elementos de esta sucesión se les llama números de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en la flora de la alcachofa, las inflorescencias del brécol romanescu y en el arreglo de un cono.
Historia
La sucesión fue descrita por Fibonacci como la solución a un problema de la cría de conejos: «Cierto hombre tenía una pareja de conejos en un lugar cerrado y deseaba saber cuántos se podrían reproducir en un año a partir de la pareja inicial teniendo en cuenta que de forma natural tienen una pareja en un mes, y que a partir del segundo se empiezan a reproducir».2
| Número de Mes | Explicación de la genealogía | Parejas de conejos totales |
|---|---|---|
| Comienzo del mes 1 | Nace una pareja de conejos (pareja A). | 1 pareja en total. |
| Fin del mes 1 | La pareja A tiene un mes de edad. Se cruza la pareja A. | 1+0=1 pareja en total. |
| Fin del mes 2 | La pareja A da a luz a la pareja B. Se vuelve a cruzar la pareja A. | 1+1=2 parejas en total. |
| Fin del mes 3 | La pareja A da a luz a la pareja C. La pareja B cumple 1 mes. Se cruzan las parejas A y B. | 2+1=3 parejas en total. |
| Fin del mes 4 | Las parejas A y B dan a luz a D y E. La pareja C cumple 1 mes. Se cruzan las parejas A, B y C. | 3+2=5 parejas en total. |
| Fin del mes 5 | A, B y C dan a luz a F, G y H. D y E cumplen un mes. Se cruzan A, B, C, D y E. | 5+3=8 parejas en total. |
| Fin del mes 6 | A, B, C, D y E dan a luz a I, J, K, L y M. F, G y H cumplen un mes. Se cruzan A, B, C, D, E, F, G y H. | 8+5=13 parejas en total. |
| … | … | … |
| … | … |
Nota: al contar la cantidad de letras distintas en cada mes, se puede saber la cantidad de parejas totales que hay hasta ese mes.
De esta manera Fibonacci presentó la sucesión en su libro Liber Abaci, publicado en 1202. Muchas propiedades de la sucesión de Fibonacci fueron descubiertas por Édouard Lucas, responsable de haberla denominado como se la conoce en la actualidad.3
También Kepler describió los números de Fibonacci, y el matemático escocés Robert Simson descubrió en 1753 que la relación entre dos números de Fibonacci sucesivos  se acerca a la relación áurea fi (
se acerca a la relación áurea fi ( ) cuanto más se acerque a infinito; es más: el cociente de dos términos sucesivos de toda sucesión recurrente de orden dos tiende al mismo límite. Esta sucesión tuvo popularidad en el siglo XX especialmente en el ámbito musical, en el que compositores con tanto renombre como Béla Bartók, Olivier Messiaen, la banda Tool y Delia Derbyshire la utilizaron para la creación de acordes y de nuevas estructuras de frases musicales.
) cuanto más se acerque a infinito; es más: el cociente de dos términos sucesivos de toda sucesión recurrente de orden dos tiende al mismo límite. Esta sucesión tuvo popularidad en el siglo XX especialmente en el ámbito musical, en el que compositores con tanto renombre como Béla Bartók, Olivier Messiaen, la banda Tool y Delia Derbyshire la utilizaron para la creación de acordes y de nuevas estructuras de frases musicales.
Definición recursiva
Los números de Fibonacci quedan definidos por la ecuación:
(3)
partiendo de dos primeros valores predeterminados:
se obtienen los siguientes números:
para 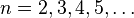
Esta manera de definir, de hecho considerada algorítmica, es usual en Matemática discreta.
Representaciones alternativas
Para analizar la sucesión de Fibonacci (y, en general, cualquier sucesión) es conveniente obtener otras maneras de representarla matemáticamente.
Función generadora
Una función generadora para una sucesión cualquiera 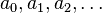 es la función
es la función 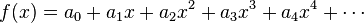 , es decir, una serie formal de potencias donde cada coeficiente es un elemento de la sucesión. Los números de Fibonacci tienen la función generadora
, es decir, una serie formal de potencias donde cada coeficiente es un elemento de la sucesión. Los números de Fibonacci tienen la función generadora
(4)
Cuando esta función se expande en potencias de  , los coeficientes resultan ser la sucesión de Fibonacci:
, los coeficientes resultan ser la sucesión de Fibonacci:
Fórmula explícita
La definición de la sucesión de Fibonacci es recurrente; es decir que se necesitan calcular varios términos anteriores para poder calcular un término específico. Se puede obtener una fórmula explícita de la sucesión de Fibonacci (que no requiere calcular términos anteriores) notando que las ecuaciones (), () y () definen la relación de recurrencia
con las condiciones iniciales
 y
y 
El polinomio característico de esta relación de recurrencia es 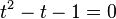 , y sus raíces son
, y sus raíces son
De esta manera, la fórmula explícita de la sucesión de Fibonacci tendrá la forma
 .4
.4
Si se toman en cuenta las condiciones iniciales, entonces las constantes  y
y  satisfacen la ecuación anterior cuando
satisfacen la ecuación anterior cuando 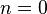 y
y 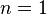 , es decir que satisfacen el sistema de ecuaciones
, es decir que satisfacen el sistema de ecuaciones
Al resolver este sistema de ecuaciones se obtiene
Por lo tanto, cada número de la sucesión de Fibonacci puede ser expresado como
(5)
Para simplificar aún más es necesario considerar el número áureo
de manera que la ecuación () se reduce a
(6)
Esta fórmula se le atribuye a Édouard Lucas, y es fácilmente demostrable por inducción matemática. A pesar de que la sucesión de Fibonacci consta únicamente de números naturales, su fórmula explícita incluye al número irracional  . De hecho, la relación con este número es estrecha.
. De hecho, la relación con este número es estrecha.
Forma matricial
Otra manera de obtener la sucesión de Fibonacci es considerando el sistema lineal de ecuaciones
Este sistema se puede representar mediante su notación matricial como
Conociendo a  y
y 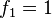 , al aplicar la fórmula anterior
, al aplicar la fórmula anterior  veces se obtiene
veces se obtiene
(7)
Una vez aquí, simplemente tenemos que diagonalizar la matriz, facilitando así la operación de potenciación, y obteniendo por tanto la fórmula explícita para la sucesión que se especificó arriba.
y más aún
(8)
Estas igualdades pueden probarse mediante inducción matemática.
Propiedades de la sucesión
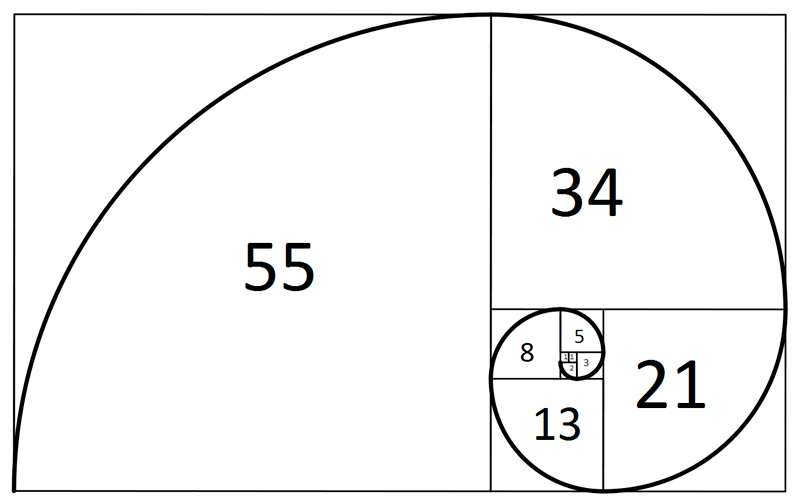
Al construir bloques cuya longitud de lado sean números de Fibonacci se obtiene un dibujo que asemeja al rectángulo áureo (véase Número áureo).
Los números de Fibonacci aparecen en numerosas aplicaciones de diferentes áreas. Por ejemplo, en modelos de la crianza de conejos o de plantas, al contar el número de cadenas de bits de longitud  que no tienen ceros consecutivos y en una vasta cantidad de contextos diferentes. De hecho, existe una publicación especializada llamada Fibonacci Quarterly5 dedicada al estudio de la sucesión de Fibonacci y temas afines. Se trata de un tributo a cuán ampliamente los números de Fibonacci aparecen en matemáticas y sus aplicaciones en otras áreas. Algunas de las propiedades de esta sucesión son las siguientes:
que no tienen ceros consecutivos y en una vasta cantidad de contextos diferentes. De hecho, existe una publicación especializada llamada Fibonacci Quarterly5 dedicada al estudio de la sucesión de Fibonacci y temas afines. Se trata de un tributo a cuán ampliamente los números de Fibonacci aparecen en matemáticas y sus aplicaciones en otras áreas. Algunas de las propiedades de esta sucesión son las siguientes:
- La razón o cociente entre un término y el inmediatamente anterior varía continuamente, pero se estabiliza en el número áureo. Es decir:
- Este límite no es privativo de la Sucesión de Fibonacci. Cualquier sucesión recurrente de orden 2, como la sucesión 3, 4, 7, 11, 18,…, lleva al mismo límite. Esto fue demostrado por Barr y Schooling en una carta publicada en la revista londinense «The Field» del 14 de diciembre de 1912. Los cocientes son oscilantes; es decir, que un cociente es menor al límite y el siguiente es mayor. Los cocientes pueden ordenarse en dos sucesiones que se aproximan asintóticamente por exceso y por defecto al valor límite.
- Cualquier número natural se puede escribir mediante la suma de un número limitado de términos de la sucesión de Fibonacci, cada uno de ellos distinto a los demás. Por ejemplo,
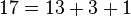 ,
, 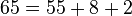 .
. - Tan sólo un término de cada tres es par, uno de cada cuatro es múltiplo de 3, uno de cada cinco es múltiplo de 5, etc. Esto se puede generalizar, de forma que la sucesión de Fibonacci es periódica en las congruencias módulo
 , para cualquier
, para cualquier  .
. - La sucesión puede expresarse mediante otra fórmula explícita llamada forma de Binet (de Jacques Binet). Si
 y
y  , entonces
, entonces
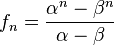 y
y 
- Cada número de Fibonacci es el promedio del término que se encuentra dos posiciones antes y el término que se encuentra una posición después. Es decir
- Lo anterior también puede expresarse así: calcular el siguiente número a uno dado es 2 veces éste número menos el número 2 posiciones más atrás.
- La suma de los
 primeros números es igual al número que ocupa la posición
primeros números es igual al número que ocupa la posición 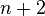 menos uno. Es decir
menos uno. Es decir
- Otras identidades interesantes incluyen las siguientes:
- Si
 , entonces
, entonces 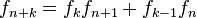 para cualquier
para cualquier 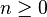
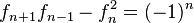 (Identidad de Cassini)
(Identidad de Cassini)
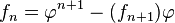 (con φ = número áureo) o, despejando f(n+1) y aplicando 1/φ = φ-1:
(con φ = número áureo) o, despejando f(n+1) y aplicando 1/φ = φ-1:
- El máximo común divisor de dos números de Fibonacci es otro número de Fibonacci. Más específicamente
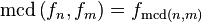
- Esto significa que
 y
y 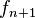 son primos relativos y que
son primos relativos y que 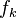 divide exactamente a
divide exactamente a 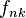
- Los números de Fibonacci aparecen al sumar las diagonales del triángulo de Pascal. Es decir que para cualquier
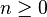 ,
,
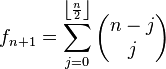
- y más aún

- Si
 , tal que
, tal que  es un número primo, entonces
es un número primo, entonces  también es un número primo, con una única excepción,
también es un número primo, con una única excepción,  ; 3 es un número primo, pero 4 no lo es.
; 3 es un número primo, pero 4 no lo es. - La suma infinita de los términos de la sucesión
 es exactamente
es exactamente 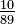 .
. - La suma de diez números Fibonacci consecutivos es siempre 11 veces superior al séptimo número de la serie.
- El último dígito de cada número se repite periódicamente cada 60 números. Los dos últimos, cada 300; a partir de ahí, se repiten cada
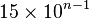 números.
números.
Generalización
El concepto fundamental de la sucesión de Fibonacci es que cada elemento es la suma de los dos anteriores. En este sentido la sucesión puede expandirse al conjunto de los números enteros como 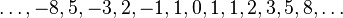 de manera que la suma de cualesquiera dos números consecutivos es el inmediato siguiente. Para poder definir los índices negativos de la sucesión, se despeja
de manera que la suma de cualesquiera dos números consecutivos es el inmediato siguiente. Para poder definir los índices negativos de la sucesión, se despeja  de la ecuación () de donde se obtiene
de la ecuación () de donde se obtiene
De esta manera, 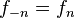 si
si  es impar y
es impar y  si
si  es par.
es par.
La sucesión se puede expandir al campo de los números reales tomando la parte real de la fórmula explícita (ecuación ()) cuando  es cualquier número real. La función resultante
es cualquier número real. La función resultante
tiene las mismas características que la sucesión de Fibonacci:

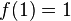
 para cualquier número real
para cualquier número real 
Una sucesión de Fibonacci generalizada es una sucesión  donde
donde
(9)
para
Es decir, cada elemento de una sucesión de Fibonacci generalizada es la suma de los dos anteriores, pero no necesariamente comienza en 0 y 1.
Una sucesión de fibonacci generalizada muy importante, es la formada por las potencias del número áureo.
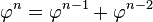 .
.
La importancia de esta sucesión reside en el hecho de que se puede expandir directamente al conjunto de los números reales.
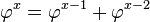 .
.
…y al de los complejos.
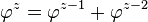 .
.
Una característica notable es que, si  es una sucesión de Fibonacci generalizada, entonces
es una sucesión de Fibonacci generalizada, entonces
Por ejemplo, la ecuación () puede generalizarse a
Esto significa que cualquier cálculo sobre una sucesión de Fibonacci generalizada se puede efectuar usando números de Fibonacci.
Sucesión de Lucas
Un ejemplo de sucesión de Fibonacci generalizada es la sucesión de Lucas, descrita por las ecuaciones


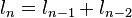 para
para 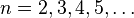
La sucesión de Lucas tiene una gran similitud con la sucesión de Fibonacci y comparte muchas de sus características. Algunas propiedades interesantes incluyen:
- La proporción entre un número de Lucas y su sucesor inmediato se aproxima al número áureo. Es decir
- La fórmula explícita para la sucesión de Lucas es
- La suma de los primeros
 números de Lucas es el número que se encuentra en la posición
números de Lucas es el número que se encuentra en la posición 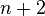 menos uno. Es decir
menos uno. Es decir
- Cualquier fórmula que contenga un número de Lucas puede expresarse en términos de números de Fibonacci mediante la igualdad
- Cualquier fórmula que contenga un número de Fibonacci puede expresarse en términos de números de Lucas mediante la igualdad
Algoritmos de cálculo
Para calcular el  -ésimo elemento de la sucesión de Fibonacci existen varios algoritmos (métodos). La definición misma puede emplearse como uno, aquí expresado en pseudocódigo:
-ésimo elemento de la sucesión de Fibonacci existen varios algoritmos (métodos). La definición misma puede emplearse como uno, aquí expresado en pseudocódigo:
Algoritmo 1 Versión recursiva (Complejidad  ) ) |
función 
|
Usando técnicas de análisis de algoritmos es posible demostrar que, a pesar de su simplicidad, el algoritmo requiere efectuar 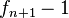 sumas para poder encontrar el resultado. Dado que la sucesión
sumas para poder encontrar el resultado. Dado que la sucesión 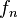 crece tan rápido como
crece tan rápido como  , entonces el algoritmo está en el orden de
, entonces el algoritmo está en el orden de  . Es decir, que este algoritmo es muy lento. Por ejemplo, para calcular
. Es decir, que este algoritmo es muy lento. Por ejemplo, para calcular  este algoritmo requiere efectuar 20.365.011.073 sumas.
este algoritmo requiere efectuar 20.365.011.073 sumas.
Para evitar hacer tantas cuentas, es común recurrir a una calculadora y utilizar la ecuación (), sin embargo, dado que  es un número irracional, la única manera de utilizar esta fórmula es utilizando una aproximación de
es un número irracional, la única manera de utilizar esta fórmula es utilizando una aproximación de  y obteniendo en consecuencia un resultado aproximado pero incorrecto. Por ejemplo, si se usa una calculadora de 10 dígitos, entonces la fórmula anterior arroja como resultado
y obteniendo en consecuencia un resultado aproximado pero incorrecto. Por ejemplo, si se usa una calculadora de 10 dígitos, entonces la fórmula anterior arroja como resultado  aún cuando el resultado correcto es
aún cuando el resultado correcto es 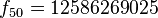 . Este error se hace cada vez más grande conforme crece
. Este error se hace cada vez más grande conforme crece  .
.
Un método más práctico evitaría calcular las mismas sumas más de una vez. Considerando un par  de números consecutivos de la sucesión de Fibonacci, el siguiente par de la sucesión es
de números consecutivos de la sucesión de Fibonacci, el siguiente par de la sucesión es 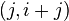 , de esta manera se divisa un algoritmo donde sólo se requiere considerar dos números consecutivos de la sucesión de Fibonacci en cada paso. Este método es el que usaríamos normalmente para hacer el cálculo a lápiz y papel. El algoritmo se expresa en pseudocódigo como:
, de esta manera se divisa un algoritmo donde sólo se requiere considerar dos números consecutivos de la sucesión de Fibonacci en cada paso. Este método es el que usaríamos normalmente para hacer el cálculo a lápiz y papel. El algoritmo se expresa en pseudocódigo como:
Algoritmo 2 Versión iterativa (Complejidad 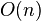 ) ) |
función 
|
Esta versión requiere efectuar sólo  sumas para calcular
sumas para calcular 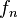 , lo cual significa que este método es considerablemente más rápido que el algoritmo . Por ejemplo, el algoritmo sólo se requiere efectuar 50 sumas para calcular
, lo cual significa que este método es considerablemente más rápido que el algoritmo . Por ejemplo, el algoritmo sólo se requiere efectuar 50 sumas para calcular  .
.
Un algoritmo todavía más rápido se sigue partiendo de la ecuación (). Utilizando leyes de exponentes es posible calcular  como
como
De esta manera se divisa el algoritmo de tipo Divide y Vencerás donde sólo se requeriría hacer, aproximadamente,  multiplicaciones matriciales. Sin embargo, no es necesario almacenar los cuatro valores de cada matriz dado que cada una tiene la forma
multiplicaciones matriciales. Sin embargo, no es necesario almacenar los cuatro valores de cada matriz dado que cada una tiene la forma
De esta manera, cada matriz queda completamente representada por los valores  y
y  , y su cuadrado se puede calcular como
, y su cuadrado se puede calcular como
Por lo tanto el algoritmo queda como sigue:
Algoritmo 3 Versión Divide y Vencerás (Complejidad  ) ) |
función 
|
A pesar de lo engorroso que parezca, este algoritmo permite reducir enormemente el número de operaciones que se necesitan para calcular números de Fibonacci muy grandes. Por ejemplo, para calcular  , en vez de hacer las 573.147.844.013.817.084.100 sumas del algoritmo o las 100 sumas con el algoritmo , el cálculo se reduce a tan sólo 9 multiplicaciones matriciales.
, en vez de hacer las 573.147.844.013.817.084.100 sumas del algoritmo o las 100 sumas con el algoritmo , el cálculo se reduce a tan sólo 9 multiplicaciones matriciales.
La sucesión de Fibonacci en la naturaleza
Los machos de una colmena de abejas tienen un árbol genealógico que cumple con esta sucesión. El hecho es que un zángano (1), el macho de la abeja, no tiene padre, pero sí que tiene una madre (1, 1), dos abuelos, que son los padres de la reina (1, 1, 2), tres bisabuelos, ya que el padre de la reina no tiene padre (1, 1, 2, 3), cinco tatarabuelos (1, 1, 2, 3, 5), ocho trastatarabuelos (1, 1, 2, 3, 5, 8) y así sucesivamente, cumpliendo con la sucesión de Fibonacci.
Recientemente, un análisis histórico-matemático acerca del contexto de Leonardo de Pisa y la proximidad de la ciudad de Bejaia, una importante exportadora de cera en los tiempos de Leonardo (de la cual se deriva el nombre en francés de esta ciudad, «Bougie», que significa «vela»), ha sugerido que fueron los criadores de abejas de Bejaia y el conocimiento de la ascendencia de las abejas lo que inspiró los números Fibonacci más que el modelo de reproducción de conejos.6
Dígitos en la sucesión de Fibonacci
Una de las curiosidades de dicha serie son los dígitos de sus elementos:
- Empezando en 1 dígito y «terminando» en infinitos, cada valor de dígito es compartido por 4, 5 o 6 números de la serie. Siendo 6 solo en el caso de 1 dígito.
- En los elementos de posición n, n10, n100,…, el número de dígitos aumenta en el mismo orden. Dando múltiples distintos para cada n.
Divisibilidad
- Sean n y m enteros positivos. Si el número n es divisible por m entonces el térmimo n-ésimo de Fibonacci es divisible por el término m-ésimo de la misma sucesión. En efecto 4 divide a 12, por tanto el término de orden cuatro, el 3 divide a 144, término de orden 12 en la cita sucesión7
- Cualquiera que sea el entero m, entre los
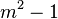 primeros números de Fibonacci habrá al menos uno divisible por m. A modo de ejemplo para m = 4, entre los primeros quince números están 8 y 144, números de Fibonacci, divisibles por 48
primeros números de Fibonacci habrá al menos uno divisible por m. A modo de ejemplo para m = 4, entre los primeros quince números están 8 y 144, números de Fibonacci, divisibles por 48 - Si k es un número compuesto diferente de 4, entonces el número k-ésimo de Fibonacci es compuesto.9 Para el caso 10, compuesto distinto de 4, el décimo número de Fibonacci 55, es compuesto.
- Los números consecutivos de Fibonacci son primos entre sí10
Véase también
Referencias
- La leyenda que motivó esta sucesión «empezó con una pareja de conejos». Vorobiov: Números de Fibonacci
- Laurence Sigler, Fibonacci’s Liber Abaci, página 404
- Handbook of discrete and combinatorial mathematics, sección 3.1.2
- Pareciera que surge de modo natural la raíz cuadrada de cinco, número irracional pura creación humana
- Fibonacci Quarterly
- (en inglés)T.C.Scott; P. Marketos (2014). «On the Origin of the Fibonacci Sequence». MacTutor History of Mathematics archive, University of St Andrews.
- Vorobiov: Números de Fibonacci, Editorial Mir, Moscú. Esta sección exige que la sucesión empiece con 1 y con 0 (1974)
- Vorobiov: Ibídem
- Vorobiov: Op. cit
- Al ojo se puede comprobar esta proposición, chequeando la lista respectiva
Bibliografía
- N. N. Vorobiov (1974). Números de Fibonacci. Editorial Mir, Moscú, Colección Lecciones Populares de Matemáticas. Traducción al español de Carlos Vega, catedrático de Matemáticas Superiores y candidato a doctor en ciencias físico-matemáticas.
- A. I. Markushevich (1974; 1981). Sucesiones recurrentes. Editorial Mir, Moscú, Colección Lecciones Populares de Matemáticas. Traducción al español de Carlos Vega.
- Luca Pacioli (1946). La Divina Proporción. Editorial Losada, Buenos Aires.
Fuente: Wikipedia.
Vincúlese a nuestras Redes Sociales:
Google+ LinkedIn YouTube Facebook Twitter
.
.




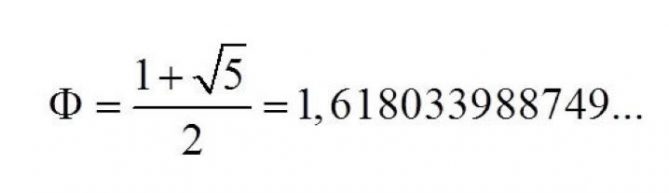

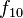
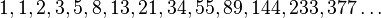


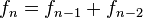




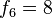
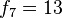
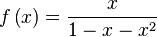
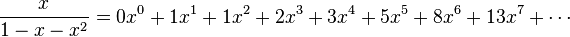
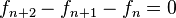
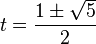

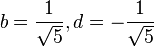
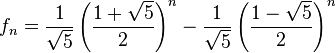
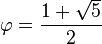
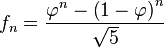
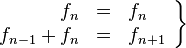
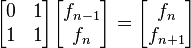

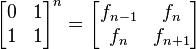

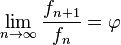
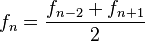




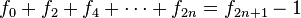
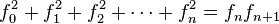
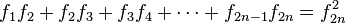

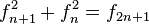
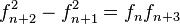
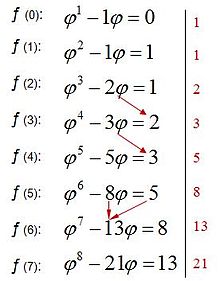
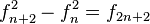



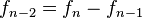
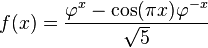

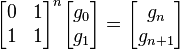

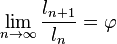

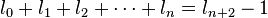



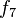 usando el algoritmo
usando el algoritmo  entonces
entonces


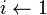

 desde
desde  hasta
hasta 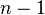 hacer
hacer



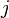

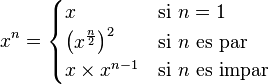
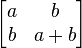

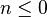 entonces
entonces

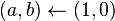

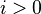 hacer
hacer
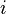 es impar entonces
es impar entonces