El Encanto Matemático: Un viaje revelador a través de Fibonacci y Zeckendorf
mayo 16, 2024 · Imprimir este artículo
Por Gustavo Ibáñez Padilla.
En el complejo y misterioso mundo de las matemáticas, hay ciertos fenómenos que capturan en forma inmediata la imaginación del público en general. Uno de esos enigmas fascinantes es la relación entre la Sucesión de Fibonacci y el Teorema de Zeckendorf. ¿Qué tienen en común estas dos joyas matemáticas? ¿Y por qué nos siguen sorprendiendo hasta el día de hoy? Lo veremos a continuación.
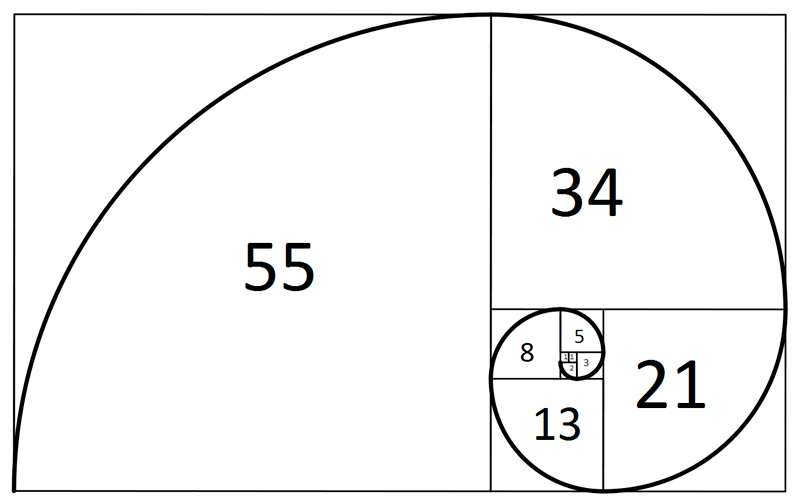
La sucesión de Fibonacci es, sin duda, una de las secuencias más famosas en el mundo de las matemáticas. Comienza con los números 0 y 1, y cada número subsiguiente es la suma de los dos anteriores. Así, la secuencia resulta ser: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, y así sucesivamente hasta el infinito. Esta secuencia aparentemente simple ha fascinado a matemáticos, artistas e incluso biólogos debido a su aparición en una enorme variedad de fenómenos naturales, desde la disposición de las hojas en una rama hasta los patrones de crecimiento de los girasoles.
La historia de la sucesión de Fibonacci se remonta al siglo XIII, a un hombre conocido como Leonardo de Pisa, comúnmente llamado Fibonacci. En su influyente libro Liber Abaci, publicado en 1202, Fibonacci presentó al mundo occidental los números indo-arábigos y sus aplicaciones en la aritmética. Pero lo que llamó la atención de muchos fue un problema aparentemente simple sobre el crecimiento de una población de conejos, que llevó al descubrimiento de la secuencia de números que ahora lleva su nombre.
¿Cuál es la relación de Fibonacci con el teorema de Zeckendorf? Pues que este teorema afirma que: Todo entero positivo se escribe, de manera única, como suma de números de Fibonacci no consecutivos. A esa escritura única se le llama la descomposición de Zeckendorf del número en cuestión.
Así pues, todos los números naturales pueden expresarse como la suma de números de Fibonacci únicos. Es decir, cada número natural puede descomponerse de manera única como una suma de números de Fibonacci, sin que ninguno de ellos se repita. Esta descomposición única es lo que hace que el teorema de Zeckendorf sea tan intrigante, ya que revela una estructura ordenada y predecible que ha fascinado a generaciones de matemáticos. ( Por ejemplo: 10= 2+8 ; 26 = 5+21 ; 43 = 1+8+34 )
El matemático francés Édouard Lucas, famoso por su trabajo en Teoría de números y sus libros de matemáticas recreativas, manifestó: “Los números de Fibonacci son como un gran cuento, lleno de sorpresas y misterios, esperando ser descubiertos”. Fue Lucas quien le puso el nombre a esta famosa sucesión, de la cual descubrió numerosas características, desde patrones geométricos hasta propiedades únicas en teoría de números.
Una de las sorpresas más asombrosas de este universo matemático es la relación entre la sucesión de Fibonacci y la proporción áurea representada por el número φ (phi), cuyo valor es aproximadamente igual a 1,618, un número misterioso que parece resonar en los rincones más profundos de la naturaleza y el arte. Como si estuvieran bailando al unísono, los números de Fibonacci revelan una conexión íntima con esta proporción divina a medida que crecen hacia el infinito, como si estuvieran siguiendo una partitura escrita en el corazón mismo de la realidad.
“Las matemáticas son la poesía del universo”, sostuvo el genial matemático David Hilbert, y en la intersección de Fibonacci y Zeckendorf, encontramos una poesía matemática que cautiva y encanta con su elegancia y misterio.
Estas sorprendentes relaciones e intersecciones entre diversos conceptos matemáticos son las que nos llevan a afirmar que las matemáticas son una verdadera unidad, lo cual llevo también a los ’modernos’ a denominarla en singular y con mayúscula, como Matemática.
“Los números de Fibonacci son como una sinfonía matemática, cada uno tocando su propia melodía única, pero juntos creando una armonía incomparable” afirmaba Lucas. ¿Qué papel desempeña el teorema de Zeckendorf en esta sinfonía matemática? Resulta que este teorema proporciona un marco ordenado y estructurado para entender cómo los números naturales se descomponen en términos de números de Fibonacci únicos. Es como si cada número natural tuviera una historia que contar, una historia que se revela a través de su descomposición en términos de esta antigua secuencia numérica.
“Las matemáticas son el arte de dar el mismo nombre a diferentes cosas”, dijo el matemático francés Henri Poincaré, y resulta evidente en la intersección de Fibonacci y Zeckendorf. A través de estas ideas aparentemente abstractas, descubrimos un mundo rico y vibrante de posibilidades matemáticas que nos desafían a mirar más allá de la superficie y explorar las profundidades del universo numérico.
Pero la diversión matemática no se detiene aquí. El teorema de Zeckendorf ha inspirado una serie de acertijos y juegos matemáticos que desafían la mente y estimulan el pensamiento creativo. Desde rompecabezas de descomposición de números hasta juegos de estrategia basados en la sucesión de Fibonacci, hay un mundo de aventuras matemáticas esperando ser exploradas por aquellos dispuestos a sumergirse en sus misterios.
Y no debemos olvidar el encanto de la matemagia, un arte que combina ilusionismo y matemáticas para crear asombrosos trucos de números y acertijos. Maestros de la matemagia como Sam Lloyd y Henry Dudeney han seducido audiencias con sus trucos ingeniosos basados en principios matemáticos, recordándonos que las matemáticas pueden ser tanto sorprendentes como entretenidas, como bien lo explica Martin Gardner en su libro Matematica, magia y misterio.
La Sucesión de Fibonacci y el Teorema de Zeckendorf nos invitan a un viaje fascinante a través del rico y sorprendente mundo de las matemáticas. Desde su aparición en la naturaleza hasta su aplicación en la teoría de números y los juegos matemáticos, estas ideas continúan maravillando y deleitando a quienes se aventuran en el emocionante viaje de descubrimiento matemático.
En palabras del prolífico matemático Paul Erdős: “Las matemáticas son como una aventura sin fin, siempre hay nuevas maravillas por descubrir”. Y en el universo de las matemáticas recreativas Fibonacci, Zeckendorf y sus seguidores están siempre listos para sorprender y extasiar a aquellos que se atreven a adentrarse en sus misterios.
Fuente: Ediciones EP, 16/05/24.
Información sobre Gustavo Ibáñez Padilla
Este artículo también ha sido publicado en Mendoza Today

Más información:
Los números en la naturaleza
Matemáticas: ¿descubrimiento o creación?
La importancia del Azar: Más allá de un juego de dados
.
.




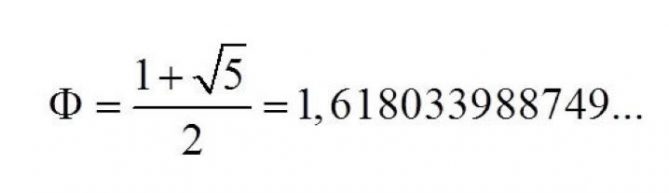

[…] El Encanto Matemático: Un viaje revelador a través de Fibonacci y Zeckendorf […]