Ciberamenzas en la infraestructura crítica

CIBERAMENAZAS, INFRAESTRUCTURA CRITICA Y EMPLEADOS POCO CAPACITADOS: UNA MEZCLA DEMOLEDORA

Por Ulises León Kandiko.

Las ciberamenazas están a la orden del día y su impacto en la sociedad cada vez es más significativo y los Estados no quedan exentos de ser víctimas, prueba de ello se ve reflejados en los portales de noticias a lo largo del año. A principio de este año (2019) se veía en el documento Estrategia Nacional de Inteligencia de los Estados Unidos de Norteamérica (USA) una advertencia sobre que “las amenazas cibernéticas supondrán un riesgo creciente para la salud pública, la seguridad y la prosperidad, ya que las tecnologías de la información se integran en infraestructura crítica, redes nacionales vitales y dispositivos de consumo», siendo un poco más traumático el Director de Inteligencia Nacional de USA, Daniel Coats, lo expresó en forma aún más sucinta: «Las luces de advertencia parpadean en rojo».

Las instalaciones de Infraestructura Crítica ya sean centrales eléctricas, ferrocarriles nacionales y sistemas subterráneos locales u otras formas de transporte público, son cada vez más objeto de ataques. Los ataques cibernéticos podrían cortar el suministro de electricidad a hospitales, hogares, escuelas y fábricas. Dependemos tanto del suministro eficiente de electricidad que su pérdida también acarrearía importantes implicaciones para otros servicios vitales. Una serie de incidentes en los últimos años demuestran no solo que la amenaza es tangible, sino también que en más de una ocasión hemos escapado de sus consecuencias como dirían los chicos del barrio «raspando», es decir de pura suerte.
Los titulares diarios destacan los últimos ataques de ransomware, violaciones de datos y nuevas técnicas de phishing, sacando a la luz una epidemia que ha resultado en daños financieros, operativos y de reputación para empresas, gobiernos y el público en general. Sin irnos muy lejos en el tiempo, hace pocos días atrás se cnfirmó un ciberataque en la Planta de Energía Nuclear Kudankulam en Tamil Nadu, India.

Hoy en día, los ataques cibernéticos ponen en riesgo mucho más que solo nuestros datos personales: los actores de amenazas han aumentado la regularidad con la que se dirigen a la infraestructura que respalda los sistemas de misión crítica, como redes eléctricas, servicios de agua, sistemas de salud, instalaciones nucleares y servicios de emergencia.

Un informe del Instituto Ponemon reveló un aumento constante de los ataques cibernéticos contra la infraestructura crítica, afirmando que «los ataques destinados a Estados/Naciones son especialmente preocupantes en el sector porque generalmente son llevados a cabo por ciberdelincuentes altamente capacitados, bien financiados y son dirigido a infraestructura crítica».

Durante el mes de Septiembre del 2019, E&E News informó sobre el primer ataque cibernético a la red eléctrica de USA, según lo identificado por North American Electric Reliability Corp. En contraste, otros sectores de infraestructura críticos como los servicios de salud y financieros han sufrido las consecuencias de los ataques cibernéticos durante más de una década, ya que la información de identificación personal que se busca regularmente puede generar millones en la Deep Web, además de los muchos beneficios asociados con el robo de propiedad intelectual.

Cuando el mundo sostuvo la respiración 3 veces
Como vimos recientemente el ciberataque en la India, también los hubo en el resto del globo, ciertamente estos ciberataques no solo se dan en plantas eléctricas, pero vale la pena referirlos ya que tienden a ser los que mas percibe la sociedad, sin dejar de lado los ciberataques que se dan en Aeropuertos, Puertos , etc. Así que acá dejo los 3 ciberataques mas significativos en Plantas generadoras de Energía.
1.    El ataque de 2010 a la Planta Nuclear de Irán en Natanz ocupa un lugar especial en los libros de historia. El llamado Malware STUXNET que hizo su primera aparición pública en ese momento, logrando detener la planta nuclear. Stuxnet fue diseñado para dañar los motores comúnmente utilizados en las centrífugas de enriquecimiento de uranio al enviarlos a girar fuera de control, logrando dejar fuera de servicio temporalmente a unas 1000 centrifugadoras.
2.    Cinco años después, en diciembre de 2015, Ucrania experimentó un asalto sin precedentes en su red eléctrica. El ataque provocó cortes de energía generalizados. Los hackers se infiltraron en 3 compañías de energía y cerraron la generación de energía temporalmente en 3 regiones de Ucrania. Dejó a casi 1/4 de millón de personas sin electricidad durante hasta 6 horas en pleno invierno. Los atacantes utilizaron el Malware BlackEnergy3 para cerrar las tres subestaciones. Se cree que el malware se entregó en correos electrónicos haciendo uso de Phishing,donde estaba oculto en archivos adjuntos falsos de Microsoft Office.
3.    El más relevante y cercano en el tiempo tuvo lugar en 2017. Los atacantes se hicieron con el control remoto de una estación de trabajo utilizando un nuevo tipo de malware, denominado Triton, para hacerse cargo del Sistema Instrumental de Seguridad (SIS) de la planta. Nuevamente, el malware se configuró específicamente para sistemas de control industrial, también conocidos como Tecnología Operativa (OT por sus siglas en inglés). Los investigadores creen que fue un acto de sabotaje destinado a provocar una explosión al deshabilitar los sistemas de seguridad diseñados para prevenir accidentes industriales catastróficos. Los ataques anteriores se han centrado en destruir datos o cerrar plantas de energía. Según algunos informes, solo un error de codificación impidió que esto sucediera. La evidencia apunta a otro ataque de phishing o spear phishing.

Ciber Seguridad de Infraestructura Crítica hoy
Como podemos ver y hemos referido en varias oportunidades, la Ciber Seguridad no es desconocida para los sectores de la Infraestructura Crítica y ciertamente para las Naciones mucho menos. En respuesta a la integración de los sistemas de tecnología de la información con los sistemas de tecnología operativa y el surgimiento de la Internet Industrial de las Cosas, en USA surgió un mayor enfoque en la mitigación de riesgos y el cumplimiento regulatorio tanto en el sector de la industria como del Gobierno Federal. Al mismo tiempo, salió a la luz un nuevo desafío: simplemente no hay suficientes trabajadores de Ciber Seguridad para cubrir la cantidad de empleos disponibles.

Para limitar el riesgo, la mayoría de las Organizaciones de Infraestructura Crítica brindan cierto nivel de capacitación en concientización de seguridad en toda la empresa, pero a menudo se limita a información muy básica, como ser ¿cómo identificar e informar un correo electrónico de phishing? Por lo general, no se brinda capacitación avanzada a los empelados comunes, y muchas áreas tangenciales pero afines de la Infraestructura Crítica nunca reciben información adecuada sobre cómo manejar las amenazas cibernéticas sospechosas.

En un mundo globalizado y de la inmediatez total, este es un problema grave, donde las vulnerabilidades y los ataques cibernéticos pueden provenir de cualquier lugar en cualquier momento, incluido un trabajador remoto, un contratista, un dispositivo o incluso la tecnología que emplea un termostato inteligente.

Esta no es la primera vez que en un artículo mío aparecen juntas las palabras ciberamenazas e Infraestructura Crítica, pero lo cierto es que nunca está demás dar un poco de perspectiva al tema, no hay que desaprovechar la oportunidad de que algún decisor lo lea y pueda cambiar algo. La gran mayoría de empresas de Infraestructura Crítica (IC) monitorean remotamente el estado y la ubicación de trenes, autobuses y camiones; pueden ajustar el flujo de petróleo crudo y gas natural a través de tuberías de forma remota; el consumo de agua y electricidad se puede controlar y cambiar desde una ubicación centralizada y los dispositivos médicos se pueden controlar desde medio mundo de distancia. Estas comodidades reducen los costos, aumentan la eficiencia y en general hacen que nuestras vidas sean más fáciles (¿será así?), pero a medida que la cantidad de sistemas interconectados continúa aumentando, también lo hace la superficie de ataque. Como resultado, más empleados en un ecosistema de IC son una amenaza, lo sepan o no, o quieran saberlo o no, no hay más ciego que el que no quiere ver.

Capacitación: ¡¡al infinito y más allá!!
Las empresas de IC no deberían seguir basando su capacitación a los empleados basándose en las campañas de concientización de seguridad cibernética pensando que su tecnología y sus equipos de seguridad son suficientes para mantener el control, creer que dar unas cartillas sobre lo que es el Phishing, no genera un buen presagio. En cambio, todos los empleados deben comenzar a comprender que cualquier interacción con la tecnología puede desempeñar un papel en un ciberataque. Esto representa un cambio tanto en la cultura como en la estrategia, que nunca es fácil de implementar a pesar de su necesidad.

En última instancia, las empresas de IC deben comenzar a enseñar a cada empleado y partes interesadas, sin importar el rol que ejecuta dentro de la misma, que el papel que desempeña en cuanto a la protección de la IC es vital, es una construcción global. El imponer tácticas de miedo es asegurar un fracaso, solo a través de compartir el conocimiento y la comprensión de cómo funcionan los ciberataques y cómo manejarlos, nos garantiza estar marchando por un buen camino.

No solo los Chief Information Security Officer´s (CISO), sino las máximas autoridades como los Chief Executive Officer´s (CEO) de las empresas de IC deben considerar algunos de los siguientes aspectos o guías:

• Capacitación Práctica: Vale más capacitar en casos prácticos y simulados a los empleados en Protección de Infraestructuras Críticas (CIP por sus siglas en inglés) que llenarlos con solo teorías y conceptos difíciles de visualizar y recordar.
• Establecer los incentivos correctos: la gestión del desempeño, la capacitación, los procesos, los procedimientos y otros sistemas para arraigar la mentalidad y los cambios culturales necesarios en lugar del temor por no cumplir las normas. 
• Capacitación orientada: capacitar en tecnologías y procesos que son valiosos para hacer que la IC sea más fuerte y resistente.  
• Liderar con el ejemplo: hacer que todos los Gerentes y Líderes en IC tomen cursos de capacitación en CIP para profundizar en la ciberseguridad de la IC y comprender cómo comunicar esa información a todos los involucrados. 

La protección de la IC contra los ataques cibernéticos es un problema de dos partes. Debemos establecer mejores protecciones, protocolos de seguridad más avanzados y mejores planes de respuesta a incidentes, pero eso comienza con un mejor conocimiento de ciberseguridad en toda la fuerza laboral afectada a la IC. En última instancia, debemos cambiar la forma en que todos en el ecosistema de IC piensan sobre la ciberseguridad. El éxito de la protección de la Infraestructura Crítica depende de los pasos tomados por la fuerza laboral para mitigar los riesgos, y eso comienza con el conocimiento y la comprensión de los matices que conforman la Ciber Seguridad del CIP. En el mundo de hoy, no puede permitirse el lujo de no capacitar a todas las partes interesadas del CIP en Ciber Seguridad.

Fuente: cxo-community.com, noviembre 2019.

---

Vincúlese a nuestras Redes Sociales:  LinkedIn      Twitter

---

.

.

La economía de la coherencia

Artículo original (traducción automática): Welcome to the Coherence Economy, 12/01/18.

Hace casi 20 años, hubo un gran cambio económico, desde una economía de servicios a una economía de experiencia. Desde entonces, el ritmo acelerado de la tecnología, impulsado por la hiperespecialización, la digitalización y la capacidad de controlar de forma programática estos nuevos entornos, ha estado introduciendo silenciosamente una nueva economía para desafiar a todas las industrias: la economía de coherencia.

Creando magia a través de la coherencia de la tecnología

Piensa en la evolución de los viajes. En la economía agraria, comenzarías a caminar; quizás podrías mejorar a un caballo. En la economía industrial, la producción en masa de automóviles y embarcaciones hizo que esas opciones fueran prácticas para una amplia gama de personas. La economía de servicios trajo aerolíneas y taxis. Algunas aerolíneas y algunos proveedores de transporte terrestre han intentado elevar sus ofertas a experiencias completas, con un éxito mixto. Pero en la economía de coherencia, sus necesidades de viaje se alinearán automáticamente en los servicios de transporte, alojamiento, gastronomía y entretenimiento, para que pueda estar en cualquier lugar en cualquier momento y vivir su vida o llevar a cabo su negocio sin interrupciones.

Imagine un conserje automático, un asistente virtual realmente inteligente, que alinea constantemente sus necesidades con las numerosas ofertas disponibles. Aunque cada elemento de su itinerario de viaje se ofrecerá por separado, la coherencia de la tecnología permitirá que los elementos funcionen en concierto, de modo que su estilo de vida global no solo sea posible, sino prácticamente sin esfuerzo.

Los ejemplos de coherencia ya nos rodean: piense en los equipos de remo que actúan como uno solo para propulsar un proyectil de carreras hacia delante. La coherencia también es abundante en la naturaleza, como las colonias de termitas que construyen estructuras fabulosas a través de comportamientos emergentes y cooperativos. La tecnología ahora permite un plano de coherencia completamente nuevo en nuestras vidas y en la economía.

Una vez que nos acostumbremos a esta coherencia, no hay vuelta atrás. Así como cada vez menos personas manejan a nuevas ubicaciones sin la red de seguridad del GPS, o depositan cheques en el banco, o compran artículos en una tienda física en lugar de tenerlos entregados a bajo costo a pedido, cada vez menos de nosotros lo pondremos con experiencias que deben ser orquestadas manualmente. Queremos magia.

Las características de la coherencia

Las principales diferencias entre la experiencia y la economía de coherencia son el alcance, la dinámica y las capas. Considere el cuidado de la salud: su objetivo final es convertirse y mantenerse lo más saludable posible. En la economía de la coherencia, los proveedores de servicios de salud estarán en el negocio para proporcionar ese resultado. En un sentido profundo, venderán la salud por sí mismos, de la misma manera que GE Aviation Systems LLC ya está vendiendo sus motores de aeronaves por hora de operación a través de sus servicios de hora de vuelo TrueChoice basados ​​en datos y análisis.

Para permitir este resultado, las compañías de servicios de salud necesitarán cambiar bastante profundamente, con un considerable replanteamiento y expansión de su alcance, su capacidad para responder a la información dinámica y su apertura para participar en un ecosistema estratificado.

Alcance

Numerosos factores afectan la salud, incluido el ejercicio, la dieta, la genética y la biometría. El cuidado de su salud es mucho más amplio que una sola experiencia: cuando su médico le pregunta si ha estado haciendo ejercicio, desea que él o ella pueda acceder al registro por minuto en su Apple Watch para obtener una imagen completa. Lograr resultados saludables significará revelar más información sobre todos los aspectos de la vida, desde el ejercicio hasta la dieta, la estabilidad emocional y cómo respondes a lo que te depare la vida: una prueba de estrés 24/7, si quieres. Y si su médico no está recabando directamente todo esto, en la mayoría de los casos, no lo estará, entonces deberá saber cómo acceder a él.

Dinámica

Cuanto más amplio sea el alcance, más dinámica se vuelve la información. Sus datos biométricos cambian constantemente y, en algunos casos, esos cambios pueden requerir atención urgente. Programar pruebas, visitas a la oficina, tratamientos y citas de seguimiento requiere sincronizar múltiples calendarios, acceder a transporte, seguir resultados y más. Si el proveedor de servicios de salud se dedica a la venta de productos de salud, tendrá que ser bueno para proporcionar toda esta coordinación, y hacerlo a escala; de hecho, esto se convertirá en el núcleo de la proposición de valor del proveedor como el manejo de beneficios y facturas. A diferencia de una experiencia única localizada en un lugar y tiempo específico, la economía de coherencia incluye un amplio espectro de escalas de tiempo (¿Qué cambia cada minuto? ¿Qué cambia cada semana?) Y plazos (¿Cómo está su pérdida de peso esta semana? ¿Qué nivel de B12 está usted? tratando de lograr durante el próximo año?), así como lugares.Por ejemplo, para reducir su incidencia de cáncer de piel, su compañía de atención médica podría realizar un seguimiento de su exposición solar acumulada y sugerir automáticamente los momentos en los que debe limitar la exposición o aplicar más protector solar, según lo que infiere de su calendario (¿Viaja a ¿Yakarta, o Edimburgo?) O datos meteorológicos.

Capas

En la economía de experiencia, las experiencias generalmente son propiedad de un único proveedor. Empresas como One Medical Group Inc. con sede en San Francisco, por ejemplo, tienen como objetivo permitir a los consumidores controlar su experiencia médica en cualquier momento desde la comodidad de sus teléfonos móviles. En la economía de la coherencia, por otro lado, la coreografía ocurre en capas. Por ejemplo, los wearables proporcionan alimentaciones crudas de ritmo cardíaco, temperatura, ritmo y más; las aplicaciones de salud las sintetizan en tendencias; la información sobre la prescripción y la ingesta de medicamentos se agrega a la imagen; los médicos hacen referencia a los sistemas de registros médicos electrónicos para armar planes de mejora de la salud, cada vez más ayudados por el aprendizaje automático; y los proveedores de seguros financian todo el paisaje de manera económica (por ejemplo, incentivando la prevención y los circuitos de retroalimentación positiva). En cada capa, los bloques de construcción en la capa inferior se unen en capacidades más útiles y de mayor valor; y existen múltiples vectores para lograr coherencia. Por ejemplo, un conjunto de síntomas puede ser analizado por varios médicos para abordar diferentes aspectos de su salud, uno que se centra en los objetivos de pérdida de peso y otro en la construcción del sistema inmunitario. La siguiente capa ofrece formas de coordinar esos planes de tratamiento, como la integración de los dos programas en uno, al tiempo que garantiza que los medicamentos no interactúen negativamente entre sí.

Coherencia: el nuevo campo de batalla

Cada cambio económico provoca grandes trastornos, y las empresas que no se ajustan a las expectativas del consumidor se quedarán atrás. Basta con mirar a Sears, Roebuck and Co. y Blockbuster Inc. La agitación de la economía de la coherencia será rápida y profunda. Las empresas deben estar armadas con velocidad, alineación y personalización.

Velocidad

Considere Amazon.com Inc. Aunque ciertamente se puede ver como un monolito, es más perspicaz verlo como una máquina de coherencia impulsada por software y conectividad. Amazon alinea a numerosos proveedores, proveedores de logística y transporte, mecanismos de comunicación y servicios digitales (por ejemplo, música, películas, libros) en un mercado en constante evolución que está tomando al sector minorista por sorpresa. Amazon está redefiniendo la velocidad a la que se espera que las empresas innoven para cumplir con las expectativas del consumidor.

Alineación

Siempre ha habido una batalla entre los mejores productos y productos todo en uno. Las tecnologías de hoy permiten una integración eficiente de las mejores ofertas para ofrecer ofertas todo en uno. Un primer ejemplo es la tecnología de marketing. Existen cientos de ofertas altamente especializadas de software como servicio para optimizar cada actividad granular en marketing, creando la necesidad de ajustes constantes para que se alineen con las campañas y evolucionen con amenazas competitivas como las guerras de precios. Si una empresa ignora estas capacidades, morirá por mil cortes. Para aprovechar estas numerosas capacidades, estrechamente enfocadas y evolucionar a medida que cambian, las empresas requieren servicios que alineen estas capacidades de forma inteligente y automática. Combinarán los feeds de datos de sus múltiples canales utilizando agregadores, medirán el ROI utilizando el software de gestión del rendimiento de marketing e integrarán y automatizarán las campañas de marketing en curso mediante el uso de plataformas de integración. Las empresas que ofrecen dicha alineación ofrecen amplitud y profundidad y tendrán una ventaja competitiva sobre las empresas tradicionales.

Personalización

Desde al menos la Revolución Industrial, gran parte de nuestro pensamiento empresarial ha sido moldeado por el simple principio de las economías de escala: cuando haces algo muchas veces de la misma manera, cada instancia se vuelve más barata. Haz un millón de camisetas y el costo de cada una debería ser menor; por lo tanto, puedes ofrecerlo por menos y ganar en el mercado. Pero, ¿qué sucede cuando cuesta lo mismo fabricar una camiseta que un millón? ¿Qué sucede cuando los costos de individualización disminuyen a cero, o al menos por debajo de los beneficios que se obtienen de ellos? Con tecnologías como la impresión 3D, las líneas de fabricación completamente automatizadas y programables, y los sistemas de logística dinámica, la economía de coherencia puede prosperar sin necesidad de economías de escala. Ziel Inc. PBC, con sede en Nueva York, por ejemplo, ofrece la fabricación de ropa a pedido con cantidades tan bajas como un artículo y los plazos de entrega medidos en días.Las empresas que aprovechan estas nuevas posibilidades no necesitan invertir en inventarios o perder tendencias a corto plazo. En cambio, pueden crear y cumplir con los picos de demanda, satisfacer las necesidades de la cola larga y experimentar sin romper el banco. Se convierten en competidores formidables.

Socio o Perecer

Es un error para las empresas pensar que pueden ser dueños de todo. Ellos no lo harán. Para prosperar en la economía de coherencia, habrá que dejar ir algunos ideales preciados, como la propiedad total del cliente. Y habrá una adopción necesaria de algunas posiciones incómodas, como la exposición de sus capacidades como interfaces de programación de aplicaciones (API) sin saber de antemano cómo se usarán.

Uber Technologies Inc., por ejemplo, se complace en respaldar cualquier uso razonable de su sistema de transporte altamente automatizado y descentralizado a través de su API Uber, API de controladores y API de entregas sin necesidad de aprobación previa. Espera que el mercado descubra nuevos usos, tales como entrega de alimentos, recompensas para conductores y más, que por supuesto impulsan nuevas fuentes de ingresos y sugieren nuevas inversiones por parte de Uber. La compañía está más que feliz de permitir a otros crear (y poseer) sus viajes de clientes impulsados ​​por su API, en lugar de tratar de retener la propiedad total del cliente.

Además, Amazon Web Services (AWS) ofrece numerosas capacidades informáticas: redes, almacenamiento, informática, administración, equilibrio de carga, monitoreo y más, completamente a pedido y completamente como componentes básicos de la API. Permite a cualquier persona, desde desarrolladores hasta grandes empresas, ensamblarlos como mejor les parezca.Incluso permite a los principales competidores de Amazon, como Netflix Inc., construir productos completos con los bloques de construcción de AWS. No intenta proteger su base de clientes de Amazon Prime Video al limitar el uso de Netflix de la plataforma AWS. Amazon se ha dado cuenta de que, en lugar de invertir en bloquear a los competidores, preferiría tomar su dinero mientras se deciden si asociarse o competir (o ambos). Después de todo, Netflix está averiguando cómo cohesionar las distintas piezas de contenido (ver experiencias, ciclos de retroalimentación e interacciones de dispositivos) en patrones de consumo altamente personalizados que se adaptan a los estilos de vida de las personas. Cualquiera que sea la combinación de bloques de construcción que resulte valiosa, es un candidato que Amazon puede ofrecer por sí solo como un nuevo producto, y que luego se convierte en un nuevo bloque (compuesto) en el que construir la próxima oferta.

Para ir un paso más allá, una red social como Facebook podría asociarse con instituciones financieras para intercambiar información con el fin de ofrecerles a los consumidores ofertas personalizadas. Facebook podría agregar las ofertas financieras de múltiples instituciones y compartirlas en fuentes de datos, convirtiéndose en un proveedor confiable de instrumentos financieros mientras mantiene a los usuarios dentro de sus paredes virtuales. Las instituciones financieras podrían recopilar información de los usuarios, como los hábitos de gasto, para inferir la intención y los objetivos de los usuarios y adquirir nuevos clientes a través de Facebook. Al final, en lugar de obligar de algún modo a los usuarios a ser clientes financieros de Facebook o de las instituciones financieras, ambos se convierten en elementos constitutivos entre sí. Después de todo, cada ensamblador de bloques de construcción se convertirá en un bloque de construcción en la asamblea de otra persona.

De la experiencia a la coherencia

Todas las etapas económicas fueron habilitadas por la tecnología, y la economía de la coherencia no es diferente. Con cientos de miles de proveedores de nicho y opciones para elegir, debe haber una forma de descubrirlos, consumirlos y reunirlos en varias combinaciones para crear nuevas ofertas.

Los habilitadores de la transición a una economía de coherencia son el software y la conectividad. El deleite cuando las cosas se alinean y «simplemente funcionan» impulsará la coherencia de la vanguardia a la corriente principal en un orden sorprendentemente corto. Hemos visto este fenómeno antes en el ascenso meteórico de automóviles, Internet y el iPhone. Una vez que lo tienes, no puedes imaginar la vida sin él. La actividad económica cambia en consecuencia.

A diferencia de la economía de experiencia, el éxito en la economía de la coherencia depende de la cooperación entre una miríada de jugadores. Los ganadores no serán los que creen ecosistemas cerrados, del tipo caracterizado por «compatible con el sistema X» o «que funcione mejor con el centro Y.» En cambio, las empresas que expongan las ofertas en formas fáciles de ensamblar y con esquemas de monetización razonables serán elegido repetidamente por otros al crear ofertas coherentes. Los consumidores notarán y elegirán las marcas que tienden a funcionar bien con todo.

De este modo, se obtendrá una gran ventaja para las empresas que facilitan el consumo de sus servicios de forma automatizada. La clave de esto es la API, el «mango» accesible por computadora por el cual se puede consumir un servicio.En la última década, ha surgido una gran cantidad de servicios para todo, desde la geolocalización hasta los pagos y el envío, todos accesibles a través de API.Hay más de 18,800 API abiertas y existen órdenes de magnitud más o se están construyendo detrás de muros empresariales.

La amplitud y profundidad de este ecosistema API está creando un efecto de red, acelerando la transición a la economía de coherencia. Un efecto de red ocurre cuando hay una red de componentes y jugadores que de alguna manera están conectados entre sí, de modo que cualquier miembro nuevo se beneficia de aquellos en la red y viceversa. No es que las redes sean fáciles de comenzar. Los primeros miembros ganan poco valor. Pero cuando las redes ganan masa crítica, son tremendamente valiosas, basta con mirar a Facebook.

Los efectos de red han jugado un papel importante en cada etapa económica y lo harán nuevamente en la economía de coherencia. Con tantos servicios disponibles como API, muchas empresas reconocen que es mucho más fácil crear ofertas coherentes mediante la construcción de redes de aplicaciones, donde las aplicaciones, los datos y los dispositivos se pueden conectar y desconectar fácilmente a medida que cambian las condiciones del mercado. Esto elimina la necesidad de tiempo y costo de construir siempre nuevos servicios y experiencias desde cero. Eso, por supuesto, incentiva a los proveedores de API y lleva a otros a crear nuevas API o exponer sus capacidades existentes a través de API. A su vez, las empresas que consumen API se dan cuenta de que deben contribuir con sus propias API para monetizar sus capacidades o, al menos, para facilitar el trabajo con ellas, y así crece el ecosistema API.

El terreno ha sido establecido para la economía de coherencia. Todas las industrias, desde la medicina hasta el marketing, la fabricación y el ejército, han desarrollado numerosas capacidades hiperespecializadas. Todos los aspectos de estas industrias se han convertido, o se están convirtiendo rápidamente, en software y en software. Los sistemas de software, sensores, actuadores y dispositivos móviles están conectados a través de redes y expuestos a través de API. Los costos han bajado. Nuestro trabajo y nuestra vida personal han estado completamente impregnados por el mundo digital, preparando el escenario para que la tecnología afecte nuestras vidas de manera mucho más profunda.

Una revolución económica ocurre no cuando una innovación se vuelve posible, sino cuando se vuelve práctica. Estamos al borde de una nueva economía.

Fuente: sloanreview.mit.edu, 12/01/18.

---

Vincúlese a nuestras Redes Sociales:

Google+      LinkedIn      YouTube      Facebook      Twitter

---

.

.

Fallo Judicial: No es delito llevar dinero para comprar dólares en una cueva

La Cámara en lo Penal Económico liberó a un hombre que llevaba dólares en su auto y dijo que eran para comprar dólares en la cueva de un amigo

Por Dolores Olveira.

La Justicia sobreseyó completamente a una persona acusada de Lavado de Dinero por transportar fondos en efectivo en su auto para, según sus propias declaraciones, comprar dólares en la «cueva» de un amigo.

En el reciente fallo «H., K. A», la sala B de la Cámara en lo Penal Económico, confirmó el sobreseimiento de una persona acusada del delito de Lavado de activos, por transportar dinero en efectivo en su vehículo para, presuntamente, cambiar dólares en una «cueva», según publicó Errepar.

Los dólares de la discordia y la causa

La causa tiene origen en una requisa policial practicada sobre el vehículo en el que se trasladaba K. A. H., a quien se detuvo al advertir que llevaba consigo dinero en efectivo que, según sus propias palabras, se trataba de «casi medio millón de pesos y estaba yendo a la cueva de un amigo a comprar dólares».

Cuando le llegaron las actuaciones policiales, la fiscalía solicitó que se encuadre la situación en la figura de lavado de activos.

Sin embargo, el Juez de primera instancia dispuso el sobreseimiento total del imputado, al considerar que no se encontraban verificados los elementos necesarios para tener por acreditado el delito.

El Juez añadió, que los antecedentes que registraba K. A. H. no habilitaban a presumir un origen ilícito al dinero secuestrado y que tampoco se encontraba acreditado que ese dinero fuera a ser introducido en el mercado a través de alguna operación que le diera origen lícito.

El juez sobreseyó en forma total al sospechoso de Lavado de dinero

El Fiscal apeló a la Cámara, por considerar que los elementos probatorios resultaban suficientes para tener por acreditado la sospecha sobre el origen ilícito del dinero

Sostuvo que «habría quedado verificada la incapacidad económica del imputado, que aquél no tendría una actividad lícita registrada, y que la suma secuestrada no estaba declarada ante el fisco nacional».

También mencionó los antecedentes penales del hombre, quien había sido condenado como partícipe secundario del delito de tenencia de estupefacientes con fines de comercialización.

La Cámara rechazó los argumentos del fiscal

Los Jueces de Cámara Roberto Hornos y Carolina Robiglio fueron en la misma línea que el Juez de la instancia previa, y confirmaron el sobreseimiento del acusado.

En su voto, la Jueza Robiglio concluyó que no se encuentra acreditado ni siquiera por indicios, que el dinero en cuestión tuviera como destino ser introducido en el mercado a través de alguna operación que le diera apariencia de origen lícito.

Agregó que no se advierten medidas de prueba pendientes de producción por las que pudiera eventualmente acreditarse el delito, por lo que la sentencia de primera instancia «resulta ajustada a derecho y debe ser confirmada».

Por su parte, el Juez Hornos puso el acento en el procedimiento policial inicial y señaló que los funcionarios policiales que participaron «no habrían actuado en el marco de las facultades prevencionales que les concede el Código Penal«.

Los policías encontraron el dinero más allá de sus potestades de prevención

«En el caso no se verifica la concurrencia de circunstancias que, objetiva y razonablemente, hayan tenido entidad suficiente para sospechar la posible comisión de hecho ilícito alguno, así como tampoco para presumir que el imputado ocultase elementos provenientes o destinados a la comisión de un delito», consideró.

Según el camarista, «no llega a comprenderse de manera acabada de qué modo el personal policial pudo advertir ‘a simple vista’ el dinero que, conforme surge del acta, se hallaba ubicado en los bolsillos de una campera que se encontraba sobre el asiento del acompañante en el interior del vehículo en el que se trasladaba K. A. H.».

Y agregó que «en tanto la tenencia de dinero en efectivo no evidencia necesariamente la comisión presunta de un hecho ilícito, no se advierte que estas circunstancias objetivas constituyeran en el caso motivos» para la actuación policial.

De este modo, la sala B de la Cámara en lo Penal Económico confirmó el sobreseimiento.

Fuente: iprofesional.com, 16/08/22

---

Más información:

Primer condenado en Argentina por Lavado de Dinero empleando Bitcoins

.

.

El mundo de los números complejos

El bello mundo de los números imposibles

El encaje de los números complejos como instrumento de gran potencia en varias ramas de matemáticas puras y aplicadas transitó por distintas fases de aceptación que fueron encabezadas por eminentes matemáticos

Por Juan Matías Sepulcre.

Los números complejos hicieron sus primeras tímidas apariciones en la escena científica a través de los trabajos del médico y matemático Girolamo Cardano (1501-1576) del matemático e ingeniero hidráulico Rafael Bombelli (1526-1572) en relación al cálculo de las raíces de un polinomio cúbico, es decir, en la búsqueda de valores exactos X0 cumpliendo relaciones de la forma:

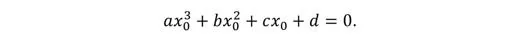
En realidad, aunque no fue la motivación principal de su aparición en escena, los números complejos ya surgen de forma explícita en las soluciones de determinadas ecuaciones cuadráticas. Por ejemplo, consideremos la ecuación: x²-2x-3=0

Que equivale a: (x+1)(x-3)=0

Resulta claro que sus soluciones son: x=-1 y x=3

Sin embargo, si consideramos la ecuación: x²+1=0

El lector puede observar que, como el cuadrado de un número real cualquiera es positivo o nulo, no es posible resolverla mediante números reales . Sin embargo, si introducimos un número que podríamos llamar la raíz cuadrada de menos uno , obtenemos algebraicamente las soluciones:

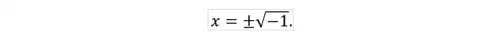
No obstante, antes de la época del renacimiento en la que se abordan las soluciones de las ecuaciones cúbicas, la aparición de la raíz de un número negativo en el análisis de cualquier ecuación, también cuadrática, llevaba inmediatamente a la interpretación de que el problema asociado a tal ecuación no presentaba solución alguna .

Hoy en día sabemos que los números complejos constituyen una herramienta esencial de trabajo de algunas ramas de matemáticas puras y aplicadas como la variable compleja, ecuaciones diferenciales, aerodinámica, hidrodinámica o electromagnetismo. De hecho, es altamente reconocida su utilidad en muchos campos del análisis matemático, álgebra, mecánica cuántica, electrónica o telecomunicaciones.

Sin embargo, podríamos decir que desde el siglo XVI hasta finales del siglo XVIII estos números fueron usados con cierto recelo y desconfianza , siendo motivo de diversas controversias entre los miembros de la comunidad científica.

De hecho, fueron inicialmente considerados como números imposibles tolerados únicamente en un limitado dominio algebraico por su utilidad complementaria para resolver ciertas ecuaciones cúbicas. Esto se debía principalmente a que, por aquel entonces, resultaba difícil concebir cualquier realidad física que correspondiese con ellos, lo que llevaba a diversos autores a emplear términos como sofisticados, sin sentido, inexplicables, incomprensibles o imposibles para referirse a tales números.

En realidad, el propio Cardano, en cuyos manuscritos aparecen raíces cuadradas de números negativos, los trataba de modo muy sutil, como un mero artefacto matemático carente de significado propio, pero dotados de algunas reglas para manipularlos. Sin embargo, tras el desarrollo de la obra Ars Magna de Cardano, Bombelli fue un paso más allá al desarrollar una cierta aritmética en torno a ellos, algo de lo que nos ocuparemos más adelante.

Números negativos e irracionales

Un proceso similar ocurrió también con los números negativos, que no fueron plenamente aceptados hasta finales del siglo XVII . Por ejemplo, el hecho de hablar de -1 piezas de fruta no conllevaba grado alguno de realismo, pero desde ese mismo punto de vista tampoco lo hubiera comportado hablar de ¾ de una persona o afirmar que las mujeres tuvieron un promedio de 2,5 hijos en algún momento dado.

Sin duda alguna, hoy en día la ausencia de los números negativos también nos resultaría inconcebible, y es que por ejemplo la posibilidad de trabajar con magnitudes negativas nos permite constantemente representar deudas, pérdidas, disminuciones … algo tan habitual como el hecho de manejar temperaturas negativas.

De hecho, todo ello nos ayuda también a interpretar con mayor claridad, y expresar algebraica y rigurosamente, resultados estadísticos como el que nos permite afirmar que la tasa de fecundidad en una cierta región se haya reducido hoy en día a la mitad si la comparamos por ejemplo con el año 1960.

Además, desde un punto de vista geométrico, si consideramos los números reales como vectores dotados de magnitud (su valor absoluto) y sentido (dependiendo del signo), entonces la multiplicación por el número negativo -1 hace cambiar de sentido el número que estamos multiplicando, lo que nos añade otra razón natural de su existencia (por cierto, el lector podrá observar más tarde, cuando tratemos la interpretación geométrica de los números complejos, que lo que haremos será establecer otras direcciones en nuestra particular brújula).

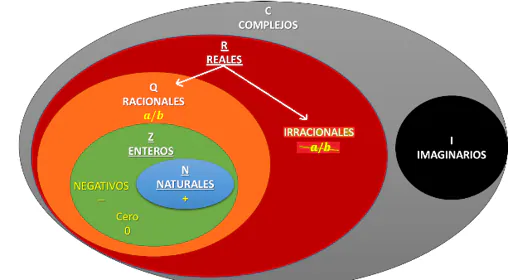
Mucho antes, en plena Grecia Clásica , el descubrimiento de que la diagonal de un cuadrado no podía expresarse como una cantidad entera de las unidades que miden los lados, esto es, la constatación de la presencia de números irracionales en tal desarrollo, llevó a la Escuela Pitagórica (en el siglo V a.C.) a una gran consternación , pues en su forma de pensar no tenían cabida las magnitudes inconmensurables .

Anque pensemos que:

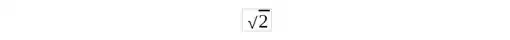
Supone una precisión de medida que es físicamente imposible, en términos prácticos no cabe duda que la existencia formal de los números irracionales, junto con todas las abstracciones teóricas realizadas hasta la fecha (incluyendo la propia simbología utilizada para los números naturales y la de los números negativos), nos han ayudado a evolucionar independientemente de su realidad física inmediata … y, desde luego, los números complejos no se escapan de este mismo contexto.

La geometría de los números complejos

Además de su aparición en la resolución de las ecuaciones cúbicas, actualmente se conoce la importancia que los números complejos tuvieron en el planteamiento y resolución de muchos problemas de la física matemática: magnetismo, calor, electricidad, gravedad, flujo de fluidos …, pero sin duda un factor que ayudó considerablemente a la plena aceptación de los números complejos fue el hecho de haber podido realizar una clara interpretación geométrica, algo que popularizó enormemente el brillante matemático Carl Friedrich Gauss (1777-1855).

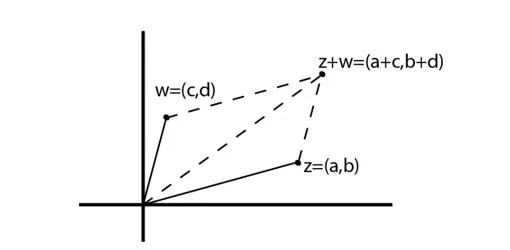
A este respecto, las coordenadas cartesianas en el plano, llamadas así en honor a René Descartes (1596-1650) por su nombre latinizado Renatus Cartesius , asocian a cada punto del plano un par de números denominados abscisa y ordenada. Así, todo número complejo puede representarse en el análogo plano bidimensional complejo como un par ordenado de números reales (a,b), donde a se denomina la parte real y b la parte imaginaria, e identificando los pares (a,0) con los números reales a , y los pares de la forma (0,b) con los llamados números imaginarios puros.

A este respecto, el par (0,1) se le denominó la unidad imaginaria , por ser de naturaleza distinta a la del número real, y es denotado por i, símbolo introducido en la literatura en 1779 por el prolífico matemático, físico y filósofo Leonhard Euler (1707-1783). Los números relacionados, es decir, aquellos de la forma a+bi, con a y b números reales, son los que llamamos números complejos y la colección de todos ello se suele denotar por C.

Aritmética de los números complejos

En el sentido anteriormente descrito, los números complejos son una extensión del sistema de los números reales y constituyen un sistema más amplio en el que cualquier polinomio de grado mayor o igual que 1 admite soluciones, resultado que se conoce con el nombre de teorema fundamental del álgebra y que logró demostrar correctamente Gauss en 1799.

Eso sí, mientras que en nuestro día a día comparamos constantemente dos números reales para decidir cuál es el mayor, esto no se puede realizar en general con los números complejos. Sin embargo, su aritmética es sencilla, ya que la suma y la multiplicación de dos números complejos es la natural, con el ingrediente extra de que cada vez que aparezca i² se reemplaza por -1 .

De hecho, si (a,b) y (c,d) representan dos números complejos arbitrarios, su suma y producto vienen dados de la siguiente manera:

(a,b)+(c,d)=(a+c,b+d),

(a,b)•(c,d)=(ac-bd, ad+bc).

Equivalentemente,

(a+bi)+(c+di)=a+c+(b+d)i,

(a+bi)•(c+di)=ac-bd+(ad+bc)i.

Resulta asequible comprobar que estas operaciones satisfacen las propiedades de conmutatividad, asociatividad y distributividad , también comunes a las operaciones con los números reales. A partir de ellas, también se pueden definir de forma coherente sus operaciones inversas, esto es la resta y la división, y otras operaciones más enmarcadas en el sistema de los números complejos como el conjugado, módulo, argumento o las raíces n -ésimas, algunas de las cuales trataremos a continuación.

Ahondando en la interpretación geométrica

A la vista de la interpretación geométrica realizada anteriormente, cualquier problema en el que las direcciones de un plano estén involucradas resulta ser una aplicación potencial de los números complejos. En particular, la física está repleta de tales interpretaciones.

A modo de ejemplo, pensemos en el fenómeno consistente en la propagación de una vibración, lo que nos conduce al concepto de onda.

Pues bien, los números complejos resultan ser una herramienta excelente para describir tales ondas como ocurre con el sonido , las olas del mar, las ondas sísmicas o la vibración de una cuerda. Prueba de ello es que si consideramos un número complejo z=a+bi, representado el plano bidimensional, siempre nos resulta posible trazar un segmento desde el origen de coordenadas (0,0) hasta el punto (a,b), sobre el que podemos calcular su longitud r (también llamado módulo de z y representado por |z|) y su ángulo α respecto del eje de abscisas (que da lugar al argumento de z). Es decir, con la ayuda de trigonometría básica, un número complejo lo podemos también representar mediante la llamada forma polar :

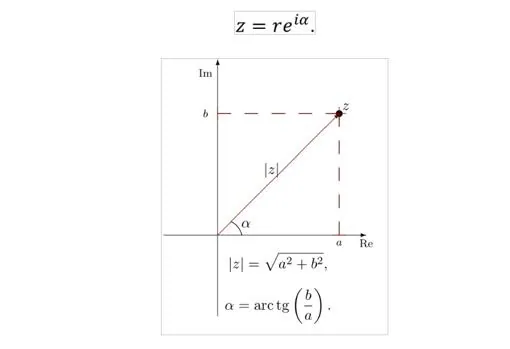
Este desarrollo nos permite inmediatamente dar una interpretación geométrica de las operaciones suma y producto introducidas anteriormente. En efecto, ya podemos afirmar que la suma de dos números complejos es equivalente a la ley del paralelogramo de vectores , y también que al multiplicar dos números complejos sus ángulos se suman, es decir:

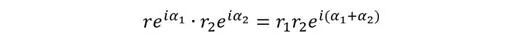
Propiedad que resulta muy útil para hacer procesamiento digital de señales, por ejemplo permitiendo rápidamente encontrar el método preciso que interviene en la variación de la fase y frecuencia de una onda, cuya descripción práctica viene dada por:

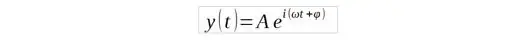
Ahora el lector podrá tratar de deducir a partir de las propiedades anteriormente expuestas la, así llamada por muchos científicos, fórmula más bella de las matemáticas , esto es, la identidad de Euler, que involucra a cinco constantes matemáticas: 0,1,e,i,π, incluyendo por tanto a la unidad imaginaria.

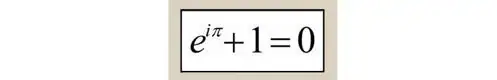
Finalmente, en este contexto conviene mencionar también los trabajos de distinta índole realizados por matemáticos como Leonhard Euler, Joseph-Louis Lagrange (1736-1813), Augustin Louis Cauchy (1789-1857), Karl Weierstrass (1815-1897) y Bernhard Riemann (1826-1866), a partir de los cuales se llegó a la plena aceptación de los números complejos como instrumento de gran potencia en el análisis intrínseco de la teoría de funciones, y en particular en la teoría de las funciones de variable compleja que constituye una de las ramas clásicas de las matemáticas que tiene sus raíces más allá del siglo XIX.

Juan Matías Sepulcre Martínez es Profesor Titular del Departamento de Matemáticas de la Universidad de Alicante. Twitter: @JMSepulcre

El ABCdario de las Matemáticas es una sección que surge de la colaboración con la Comisión de Divulgación de la de la Real Sociedad Matemática Española (RSME).

Fuente: abc.es

---

Más información:

Matemáticas: ¿descubrimiento o creación?

Martin Gardner, genio de las Matemáticas Recreativas

Un algoritmo de aprendizaje automático (IA) refuta cinco conjeturas matemáticas sin ayuda humana

.

.

La suspensión de juicio a prueba y la comisión de otro delito como causal de su revocación

Por Javier R. Casubon.

Consideraciones actuales sobre la suspensión de juicio a prueba y la comisión de otro delito como causal de su revocación.

“Anden siempre asidas de las manos la justicia y la clemencia, tan unidas, que sean como partes del mismo cuerpo; usando con tal arte la una, que la otra no quede ofendida.”
Diego de Saavedra Fajardo

SUMARIO:

1. Introducción a la suspensión de juicio a prueba: cuestiones generales y conceptuales.

2. El otorgamiento y revocación de la suspensión del juicio a prueba: la problemática acerca de la comisión de un nuevo delito y la reincidencia.

3. La revocación de la suspensión de juicio a prueba por la comisión de un delito ulterior: el supuesto fáctico y la divergencia jurisprudencial.

4. Qué debe entenderse por “comisión de nuevo delito” en el tiempo a efectos de la revocación de la suspensión del juicio a prueba.

5. La buena práctica judicial: la paralización de la suspensión de juicio a prueba sin declaración de la extinción de la acción penal ni activación de la prescripción.

6. Conclusión: una solución judicial ecléctica y equitativa frente a un problema jurídico-procesal y la demanda de una respuesta legislativa.

Artículo completo (PDF):

Fuente: Revista «El Derecho Penal», julio 2022, nº 71.

---

.

.

Las Finanzas del siglo XXI

La revolución del mundo de las Finanzas le abrió las puertas al inversor individual permitiéndole acceder a los más sofisticados instrumentos de la Planificación Financiera. Para asegurar las mejores prácticas en esta disciplina surgió la Norma ISO 22.222.

Artículo completo:  Las Finanzas en el siglo XXI v2022

.

---

Más información:

Errores comunes al invertir

---

¿Quién cuidará al abuelo?