Descifrando el Laberinto Empresarial: La danza de los cuatro elementos
abril 11, 2024
Por Gustavo Ibáñez Padilla.
En el telón de fondo del teatro empresarial, se despliega una danza enmarañada y misteriosa, una coreografía que desafía las leyes de la lógica y la previsibilidad. Esta danza, queridos lectores, es la danza de los cuatro elementos: el Principio de Peter, la Ley de Parkinson, la Ley de Murphy y la Matriz de Eisenhower. Estos no son simplemente conceptos abstractos, sino fuerzas cósmicas que influyen en el destino de las empresas y los individuos que las componen. ¿Listos para sumergirse en este baile de destinos y decisiones? ¡Ajusten sus cinturones, aférrense a sus asientos y prepárense para un viaje por el tumultuoso mundo del management!
Comencemos por el Principio de Peter, esa deliciosa paradoja que afirma que “en una jerarquía, todo empleado tiende a ascender hasta su nivel de incompetencia”. Esta joya de la psicología organizacional nos recuerda que el éxito no garantiza la competencia y que el ascenso dentro de una organización puede llevarnos a terrenos desconocidos y desafiantes. Pero no solo lo digo yo, ¡también lo afirma el incomparable Peter Drucker, el padre del management moderno! Como él solía decir: “La gerencia es hacer las cosas bien; el liderazgo es hacer las cosas correctas”.
Imaginemos a Victoria, una talentosa ingeniera que siempre ha destacado en su trabajo técnico. Su habilidad para resolver problemas y su ingenio la llevan a ser promovida como jefa de departamento. Sin embargo, una vez en el puesto, se encuentra luchando con la gestión de equipos y la diplomacia interdepartamental. ¡Ah, el dulce sabor del ascenso seguido de una caída abrupta!
.
Pero no se vayan todavía, porque la Ley de Parkinson está lista para hacer su entrada triunfal. Esta ley, formulada por el célebre Cyril Northcote Parkinson, sostiene que “el trabajo se expande hasta llenar el tiempo disponible para su realización”. ¡Ah, qué brillante observación sobre la procrastinación humana! ¿Quién no ha experimentado la sensación de que una tarea se vuelve más compleja y demorada a medida que se acerca su fecha límite?
Imaginen a Alfonso, un contador encargado de preparar un informe financiero mensual. A pesar de que podría completarlo en un par de días, decide tomarse toda la semana para hacerlo. ¿Por qué? Porque, según Parkinson, el trabajo se extenderá para llenar el tiempo disponible. ¡Ah, la dulce melodía de la procrastinación y el estrés laboral!
.
Pero no podemos olvidar la Ley de Murphy, ese despiadado dictamen que proclama que “todo lo que pueda salir mal, saldrá mal”. Esta ley, enunciada por el ingeniero aeroespacial Edward A. Murphy Jr., es un recordatorio implacable de la fragilidad de nuestros mejores planes y la inevitabilidad del caos en el mundo empresarial. Como dijo una vez el brillante empresario Elon Musk: “Si las cosas no están fallando, no estás innovando lo suficiente.”
Imaginen a Carolina, una diseñadora de moda que ha trabajado durante meses en una colección para un importante desfile. Todo está perfectamente coordinado: los diseños son innovadores, las telas son exquisitas y los modelos están listos para desfilar. Sin embargo, el día del evento, una tormenta repentina causa estragos en el transporte de las modelos y una de las máquinas de coser se descompone. ¡Gracias, Murphy, por tu inquebrantable sentido del humor!
.
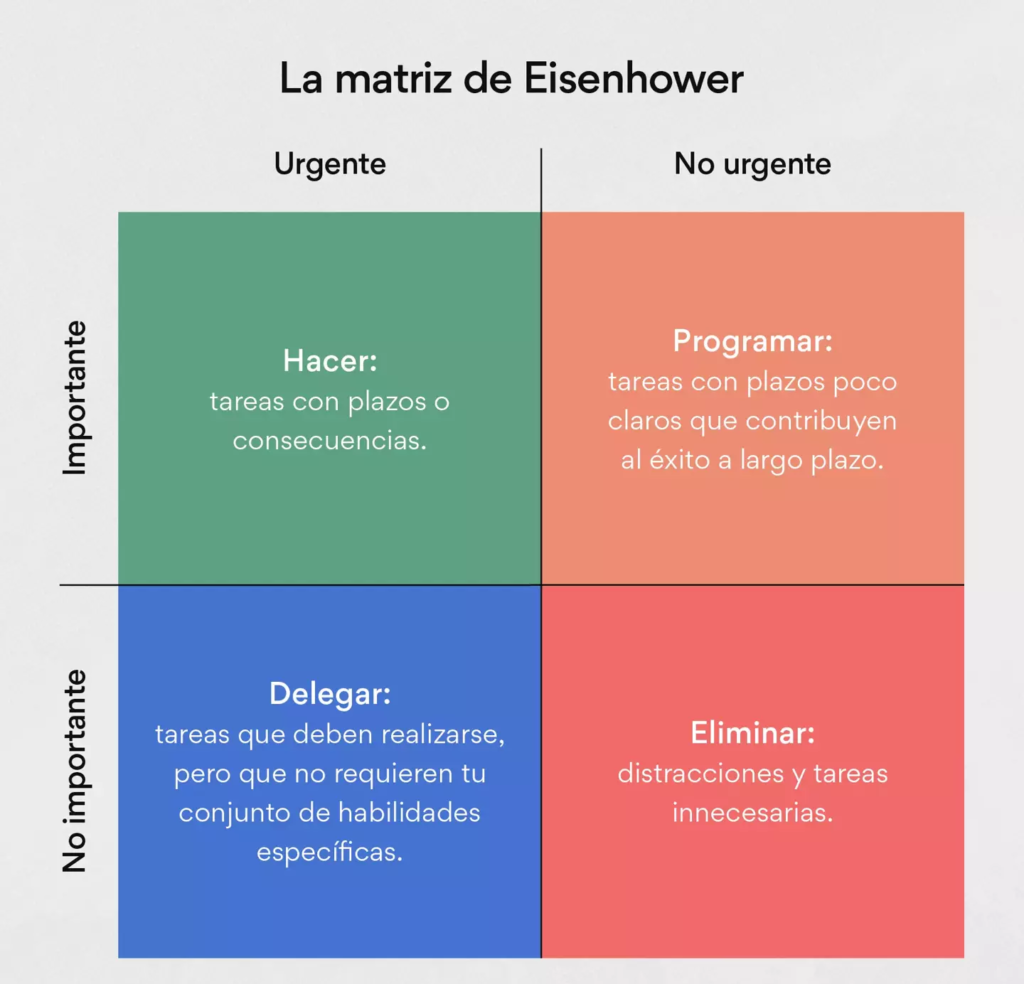
Pero en medio de este caos y confusión, emerge la Matriz de Eisenhower como un faro de sabiduría y claridad. Esta herramienta de gestión, popularizada por el presidente Dwight D. Eisenhower, nos enseña a distinguir entre lo urgente y lo importante, permitiéndonos priorizar nuestras tareas y enfocarnos en lo que realmente importa. Como recalcaba Eisenhower: “Lo importante es rara vez urgente y lo urgente es rara vez importante”.
.
Imaginen a Geraldo, un ejecutivo de ventas abrumado por una montaña de correos electrónicos y reuniones. Utilizando la Matriz de Eisenhower, identifica las tareas importantes pero no urgentes que requieren su atención a largo plazo. Luego, asigna las tareas importantes y urgentes a su equipo operativo y delega las tareas urgentes pero no importantes a su equipo de auxiliares. Por último, elimina las tareas que no son ni importantes ni urgentes. ¡Y así, recupera el control sobre su tiempo y su agenda!
Pero hay otro factor crítico en este intrincado juego empresarial, y ese es el Azar. A menudo subestimado pero siempre presente, el azar puede influir en el curso de nuestras vidas y carreras de maneras impredecibles e inesperadas. Como dijo una vez el escritor francés Jean Cocteau: “La suerte es la forma en que el azar se disfraza de destino”. Reconocer la influencia del azar en nuestras vidas nos ayuda a mantener una humildad saludable y a prepararnos para lo inesperado.
.
Entonces, ¿cómo podemos aplicar estos cuatro elementos para mejorar nuestro desempeño profesional y empresarial? Primero, reconociendo que el éxito no es solo ascender la escalera corporativa, sino también saber cuándo detenerse y reflexionar sobre nuestras habilidades y limitaciones. Segundo, comprendiendo que el tiempo es un recurso finito y que debemos utilizarlo sabiamente, priorizando nuestras tareas y enfocándonos en lo que realmente importa. Tercero, aceptando que las cosas saldrán mal en ocasiones, pero que podemos prepararnos para ello mediante una planificación cuidadosa y una actitud resiliente. Y cuarto, recordando que el azar puede jugar un papel importante en nuestras vidas y carreras, y que debemos estar preparados para adaptarnos a las circunstancias cambiantes.
En resumen, en el fascinante y complejo mundo del management y los negocios, el Principio de Peter, la Ley de Parkinson, la Ley de Murphy, la Matriz de Eisenhower y el azar son como los elementos de un ballet empresarial, cada uno contribuyendo a la danza de la vida empresarial de manera única y poderosa. ¡Así que bailemos con gracia, enfrentemos los desafíos con determinación y recordemos siempre mantener nuestros ojos en el premio!
Fuente: Ediciones EP, 11/04/24.
Información sobre Gustavo Ibáñez Padilla
Este artículo también ha sido publicado en Mendoza Today
Más información:
La Teoría de la estupidez según Cipolla
La importancia del Azar: Más allá de un juego de dados
La influencia de la Opinión Ajena en la sociedad moderna
.
.
La importancia del Azar: Más allá de un juego de dados
noviembre 17, 2023
Por Gustavo Ibáñez Padilla.
Álea iacta est – la suerte está echada. Estas palabras, atribuidas a Julio César en el crucial momento en que cruzó el río Rubicón, resonaron a lo largo de la historia como un recordatorio de que la vida está impregnada de elementos impredecibles. Hoy, en el siglo XXI, el concepto de azar cobra especial relevancia, por lo que resulta de gran interés explorar su papel en nuestras decisiones y considerar su presencia constante en eventos aparentemente insignificantes.
.
La aleatoriedad, definida como la imprevisibilidad inherente a ciertos eventos, procesos o modelos, encuentra su lugar en diversas disciplinas, desde las matemáticas hasta la filosofía y la física cuántica. En el vasto tablero de la existencia, cada lanzamiento de dados representa un encuentro con lo incierto.
En el ámbito matemático, se plantea una interesante paradoja: solo una secuencia infinita puede considerarse verdaderamente aleatoria. Para secuencias finitas, la influencia de un determinismo subyacente se hace evidente, ya que siempre es posible encontrar una fórmula que las reproduzca. Sin embargo, en la física cuántica, se postula una aleatoriedad profunda, desafiando nuestra capacidad de prever los resultados incluso en eventos macroscópicos como el lanzamiento de dados.
Blaise Pascal, Pierre de Fermat, Christiaan Huygens y Jacob Bernoulli, pioneros en la exploración de la probabilidad, sentaron las bases de lo que hoy conocemos como Teoría de Probabilidad. Estos visionarios matemáticos avanzaron en la comprensión de la aleatoriedad estadística, considerando las frecuencias de bloque como medida de lo impredecible.
.
La historia de la aleatoriedad se entrelaza con la eterna disyuntiva entre el libre albedrío y el determinismo. A lo largo de milenios, la filosofía y la teología han debatido sobre la autonomía de nuestras decisiones frente a un destino predestinado. Es en este diálogo entre lo impredecible y lo inevitable donde la aleatoriedad ocupa un papel crucial.
El término ‘aleatorio’ no solo denota la carencia de propósito, causa u orden, sino que también se asocia con propiedades estadísticas medibles, como la ausencia de tendencias o correlaciones identificables. En este sentido, la aleatoriedad se manifiesta como un fenómeno que trasciende la casualidad, influenciando tanto la ciencia como la historia.
A medida que avanzamos en la comprensión de la aleatoriedad, la Teoría de la información introduce la entropía como una medida de desorden, y los matemáticos Gregory Chaitin, Andréi Kolmogórov y Ray Solomonoff aportan la noción de aleatoriedad algorítmica. En este enfoque, la imprevisibilidad de una secuencia se relaciona con su capacidad para resistir la compresión algorítmica, desafiando la idea de un universo regido por patrones predefinidos. A pesar de ello cabe aquí recordar la frase del genial Albert Einstein: “Dios no juega a los dados”.
.
Pero, ¿cómo afecta el azar a nuestras vidas cotidianas? En situaciones aparentemente mundanas, como elegir una ruta para el trabajo o decidir qué película ver, la aleatoriedad se manifiesta. Tomemos el ejemplo de las aplicaciones de navegación: cada vez que confiamos en ellas para dirigirnos, confiamos en algoritmos que incorporan elementos de azar en la búsqueda de la ruta más eficiente. Detrás de la aparente simplicidad de estas decisiones se encuentra la complejidad de lo impredecible.
Incluso en la toma de decisiones más trascendentales, como elegir una carrera o a la pareja de vida, la influencia del azar no puede subestimarse. La vida está llena de giros inesperados, encuentros fortuitos y oportunidades que surgen sin previo aviso. En palabras de Nassim Taleb, autor de El Cisne Negro, la vida está llena de eventos altamente improbables que desafían nuestras expectativas y definen nuestro destino.
.
En última instancia, la importancia del azar en nuestra vida radica en su capacidad para desafiar nuestras certezas y abrir puertas a lo inexplorado. Al reconocer la presencia constante de la aleatoriedad, podemos abrazar la incertidumbre como parte integral de nuestra existencia. Cada paso que damos, cada decisión que tomamos, se convierte en una apuesta contra las probabilidades, recordándonos que, al igual que Julio César al cruzar el Rubicón, estamos echando el dado de la vida.
En un mundo cada vez más complejo e interconectado, la comprensión de la aleatoriedad se convierte en una herramienta invaluable. Nos permite adaptarnos a lo inesperado, encontrar oportunidades en los desafíos y abrazar la diversidad de experiencias que la vida tiene para ofrecer. En última instancia, la suerte puede estar echada, pero cómo enfrentamos la incertidumbre y aprovechamos las oportunidades que se presentan es el verdadero juego que define nuestra historia.
Fuente: Ediciones EP, 17/11/23.
Información sobre Gustavo Ibáñez Padilla
Más información:
Matemáticas y juegos de azar
Medidas de Tendencia Central en el Mundo Financiero
La Regresión a la Media y la Ley de los Grandes Números: Su Impacto en las Finanzas y la Gestión del Riesgo
.
.
Las matemáticas lo hicieron millonario
enero 20, 2023
El matemático que encontró un fallo en la Lotería con el que ganó millones
Durante casi una década, Jerry Selbee compró cantidades ingentes de boletos sabiendo que casi siempre saldría ganando. Así es como consiguió ‘hackear’ el sistema.
Por Héctor G. Barnés.
Marge and Jerry Selbee
Hace alrededor de una década, los dependientes de los establecimientos de alimentación del Estado de Michigan tuvieron que acostumbrarse a la fuerza a contemplar una peculiar estampa. Uno de sus vecinos, un varón de alrededor unos 65 años, entraba en su tienda y comenzaba a comprar lotería de una de las máquinas automáticas. No un billete ni dos, ni siquiera 20 ni 30 (lo que sería una cifra muy superior a la que solían adquirir la mayoría de jugadores), sino miles de décimos. Todos los que fuesen posible entre la hora de apertura de la tienda y la de cierre. No era un problema. Al fin y al cabo, este hombre, que había abierto a mediados de los años 80 otra tienda de alimentación semejante, podía llegar a gastarse miles de dólares.
Lo que no sabían los vecinos de la localidad de Evart es que no era una simple excentricidad, sino que la inversión que este misterioso jubilado estaba llevando a cabo le estaba reportando a él y a su red de colaboradores cuantiosas ganancias. A lo largo de los años, un punto negro en dos distintos sorteos les permitiría recaudar alrededor de 27 millones de dólares (unos 21 millones de euros). En la cabeza de Jerry Selbee, el matemático que trabajó para Kellogg y fue capaz de encontrar este fallo en cuestión de minutos una mañana de 2003, cuando cayó en sus manos un boleto con las probabilidades de ganar, no cabía posibilidad de que se tratase de un error. Era tan evidente que, probablemente, las autoridades sabían que nadie caería en la cuenta.
Hizo cálculos y descubrió que, en las semanas de bote, las probabilidades de obtener premio hacían que la inversión fuese siempre rentable.
¿Cuál era exactamente el truco, desvelado para el gran público por primera vez en una serie de artículos del departamento de investigación de The Boston Globe (sí, los mismos de ‘Spotlight’)? El funcionamiento del bote, en principio no tan diferente al de otros juegos españoles como la Primitiva. El coste de una papeleta de Winfall, en la que había que elegir seis número del 1 al 49, costaba un dólar. Según la cantidad de números acertados (de tres a seis), se obtendría un premio en consonancia. La clave, no obstante, se encontraba en el bote, que se repartía en caso de que tras varias semanas (seis de media) nadie hubiese acertado la combinación ganadora y se hubiesen alcanzado los cinco millones de dólares.
Cuando esto ocurría, la lotería era promocionada a todo trapo para que los jugadores casuales probasen suerte. En lo que pocas (o ninguna) persona había caído es en que, siempre y cuando nadie acertase los seis números, las probabilidades hacían que la inversión fuera siempre rentable para el jugador. Había una posibilidad entre 54 de acertar tres números y 1 en 1.500 de acertar cuatro; en las semanas en las que se repartía el bote, los premios se multiplicaban por 10, de forma que cualquier dólar invertido valía, estadísticamente, más que un dólar. Como ha explicado años después el propio Jerry a ‘The Huffington Post’ en el reportaje definitivo sobre el tema, “simplemente lo multipliqué y me dije ‘vaya, el retorno es positivo’”.
Un juego con truco
El jugador, por supuesto, seguía teniendo más posibilidades de perder que de ganar si compraba un único billete. El truco se encontraba en comprar grandes cantidades de boletos para que todos los aciertos compensasen el dinero que se perdía con las apuestas no ganadoras; cuanto más dinero uno se gastase, más posibilidades había de obtener ganancias, puesto que las estadísticas estaban a su favor. A la larga, era una simple cuestión de estadística. Algo de cajón para Jerry Selbee, un gran aficionado a las matemáticas y a los puzzles lógicos que averiguó con un sencillo vistazo que, en el caso del Winfall, la banca no ganaba.
La siguiente semana, volvió a Mesick. Se gastó 3.400 dólares y ganó 6.300. Una vez más, volvió a probar y obtuvo 15.700 dólares tras apostar 8.000
Lo más difícil, en este caso, era la logística. Al principio, porque Jerry temía contárselo a su mujer Marge, que siempre había estado en contra del juego. Así que decidió probar suerte por su cuenta, después de hacer pruebas con papel y lápiz: la primera vez se gastó 2.200 dólares en una pequeña tienda en Mesick, a unos 70 kilómetros de Evart, donde vivía. La jugada no salió bien y tan solo obtuvo 2.150 dólares; es decir, había perdido 50. Sin embargo, el matemático aficionado sabía que era una mera cuestión de mala suerte; el problema radicaba en que no se había gastado suficiente dinero. Así que la siguiente semana de bote, volvió a Mesick y se gastó 3.400 dólares: ganó 6.300. Una vez más, volvió a probar y obtuvo 15.700 dólares tras apostar 8.000. Había hackeado el sistema.
Con esa cantidad de dinero entre sus manos, no le resultó difícil convencer a su mujer que habían dado con el negocio de sus vidas. Esta se prestó a participar, entre otras razones, porque confiaba plenamente en las habilidades con los números de su marido. El problema era, en todo caso, práctico: solo se podían imprimir 10 boletos a la vez, lo que obligaba a la pareja a pasar horas y horas delante de las máquinas expendedoras y la curiosa mirada de los tenderos que, no obstante, no hacían muchas preguntas cuando veían a Jerry y Marge imprimiendo boletos sin parar. Otra aparente dificultad era ordenar estos tickets y comprobar si tenían premio o no, algo que hacían dos veces por si se habían equivocado. Un trabajo arduo que, no obstante, les mantenía entretenidos en los años previos a su jubilación.
Décimo de Powerball, un juego similar al que el matemático aficionado ‘hackeó’.
El sistema funcionaba, así que los Selbee preguntaron a sus hijos si querían unirse. En la primera apuesta perdieron 18.000 dólares, pero los descendientes de Jerry sabían bien que su padre no estaba equivocado. GS Investment Strategies fue el nombre que recibió la empresa fundada por este para administrar el dinero de los jugadores: hasta 25 personas llegaron a formar parte del club, incluidos abogados, trabajadores de una sucursal bancaria y policías. En 2005, las ganancias rondaban los 40.000 dólares. Entonces llegó la primera mala noticia: en mayo de ese año, la Lotería de Michigan cerró el concurso y dejó a la pareja de jubilados sin su principal ‘hobby’ y fuente de ingresos.
No pasaría ni un mes hasta que encontraron una alternativa parecida, eso sí, en el vecino estado de Massachusetts. Se trataba de un juego que funcionaba de forma similar, aunque con pequeñas diferencias como el coste del billete (dos dólares y no uno) o los números a elegir. La logística era aún más difícil que en el otro juego, pero eso no les disuadió de seguir con su plan, esta vez, con base en un motel al oeste del Estado. Era un trabajo intensivo: para contar todos los boletos (que en ocasiones ascendían a 70.000 dólares por sorteo), tenían que trabajar 10 horas durante 10 días. En su apuesta récord, llegaron a gastar 720.000 dólares en un único juego. La banca, a la larga, siempre perdía. Sin embargo, no eran los únicos que habían descubierto este fallo en el sistema.
Yayos vs universitarios
Ya lo contamos en su día: un grupo de alumnos del MIT había encontrado por su cuenta el mismo fallo en el sistema que este par de dependientes. No obstante, su sistema tenía una diferencia fundamental, una línea que Jerry y Maggie no se habrían atrevido a cruzar. No solo gastaban mucho dinero en boletos sabiendo que tenían la estadística de su lado, sino que también forzaban que saliese el bote apostando mucho más dinero. Jerry se enfadó tras conocer las artimañas de sus competidores. “Nos habían sacado del juego intencionadamente”, lamenta años después. El hombre hizo caso omiso cuando le propusieron intercambiar información para no pisarse los unos a los otros.
Jerry se enfadó cuando la prensa le consideró poco menos que un estafador. Él sabía que no estaba reduciendo las posibilidades de ganar de los demás
Fue también el principio del fin. No fue la autoridad lotera la que dio la estacada a este sistema, sino una periodista del equipo de investigación de The Boston Globe llamada Andrea Estes, que descubrió el truco en una serie de artículos publicados en verano de 2011, que una vez más, enfurecieron a Jerry porque le presentaba como poco menos que un estafador. Algo que él tenía muy claro que no era: matemáticamente, era consciente de que no estaba reduciendo las posibilidades de ningún competidor. Tan solo estaba aprovechando el azar en su favor. Fue una bomba informativa que pronto llegó a toda la prensa americana y que obligó a las autoridades del Estado a tomar cartas en el asunto.
La última partida jugada por la pareja tuvo lugar en enero de 2012, medio año después de la publicación del primero de los artículos. Desde luego, había sido el negocio de su vida, ya que en nueve años llegaron a obtener 27 millones de dólares (U$S 7,75 millones de ganancias, después de descontar impuestos y los costes del juego), una cantidad que terminaron repartiendo entre todos los socios de GS Investment. Sin embargo, Jerry seguía enfadado por su recién adquirida fama de ‘hacker’ lotero, y no quedó tranquilo hasta que el inspector general de Massachusetts publicó un informe de 35 páginas en el que concedía que nadie había salido perjudicado por la particular estrategia del matrimonio y sus competidores del MIT.
Lo que Jerry demostró es que quien hace la ley hace la trampa, y que muchos de los juegos de azar en los que participamos no están tan bien diseñados como parece… O incluso que estos cambios, en lugar de corromper la competición, pueden ser una manera más justa de administrar el dinero. Porque esa es la última lección de la historia de Jerry y Maggie: que la Lotería puede pasar de ser un juego que grava a los más pobres, que son los que suelen participar en esta clase de juegos, para ser una herramienta de redistribución económica… aunque sea tan solo para un puñado de lúcidos matemáticos.
Fuente: elconfidencial.com, 06/03/18.
Vincúlese a nuestras Redes Sociales: LinkedIn YouTube Twitter
.
.
Frágil, robusto y antifrágil
noviembre 27, 2019
Resumen del libro Antifrágil, de Nassim Nicholas Taleb.
La tríada: frágil, robusto y antifrágil
Pensemos en algo frágil, algún objeto de nuestra sala de estar, como el televisor o la porcelana del aparador. Si los etiquetamos como “frágiles” significa, necesariamente, que queremos que gocen tranquilidad, orden y previsibilidad. A un objeto frágil no le sentará nada bien un terremoto ni la visita de un sobrino hiperactivo. Todo lo que aborrece la volatilidad aborrece los agentes estresantes (estresores), el daño, el caos, los sucesos, el desorden, las consecuencias imprevistas, la incertidumbre y, por encima de todo, el tiempo.En el lado opuesto a lo frágil hay cosas que se benefician de las crisis; prosperan y crecen al verse expuestas a la volatilidad, al azar, al desorden y a los estresores, y les encanta la aventura, el riesgo y la incertidumbre.Pero, a pesar de la omnipresencia de este fenómeno, no existe una palabra que designe exactamente lo contrario de lo frágil. Aquí lo llamaremos antifrágil. Pensemos, por ejemplo, en Suiza, el lugar más antifrágil del planeta, ya que se beneficia de las crisis que se dan en el resto del mundo.La antifragilidad es más que resiliencia o robustez. Lo robusto aguanta los choques y sigue igual; lo antifrágil mejora. Esta propiedad se halla detrás de todo lo que ha cambiado con el tiempo: las revoluciones, la innovación tecnológica, el éxito cultural, la supervivencia empresarial, las buenas recetas de cocina, el ascenso de ciudades, las bacterias resistentes… incluso nuestra existencia como especie.La antifragilidad es relativa a una situación dada. Un boxeador puede ser robusto, sano en lo que se refiere a su condición física, y puede mejorar de un combate al siguiente, pero podría ser emocionalmente frágil y romper a llorar si su novia lo dejara. Nuestras abuelas podrían tener o haber tenido unas cualidades opuestas: una complexión frágil y una fuerte personalidad.El objetivo último de este libro es descubrir aquellas reglas que nos permitan pasar de lo frágil a lo antifrágil reduciendo la fragilidad o controlando la antifragilidad.
Lo antifrágil se beneficia de los estresores
Cuando algo no vivo se somete a estrés, sufre fatiga o se rompe. Nuestra casa o la mesa de nuestro despacho se acabarán gastando y no podrán repararse por sí solas. Puede que sean robustas, pero no pueden ser intrínsecamente antifrágiles.Por el contrario, los seres vivos y los sistemas complejos se comportan de una forma muy diferente. Están formados por componentes que interaccionan entre sí, intercambiando información por medio de estresores. Y precisamente por eso, pueden llegar a ser antifrágiles.Pensemos en el ser humano. Nuestro cuerpo no obtiene información sobre el entorno por medio del sistema lógico, la inteligencia o la capacidad de razonar y calcular, sino por medio del estrés y de las hormonas u otros mensajeros que aún están por descubrir. Los huesos del cuerpo, por ejemplo, se refuerzan cuando se ven sometidos a la gravedad, por ejemplo después de hacer ejercicio. Y del mismo modo que pasarse un mes en la cama provoca atrofia muscular, los sistemas complejos se debilitan si se ven privados de estresores.Me gusta el ejemplo de la adquisición del lenguaje: no sé de nadie que haya aprendido su lengua materna estudiando gramática y sometiéndose a exámenes cada dos por tres. Adquirimos mejor una lengua cometiendo errores, cuando debemos comunicarnos en circunstancias más o menos difíciles.El problema es que gran parte de nuestro mundo moderno tan estructurado nos ha estado perjudicando con artilugios y políticas desde arriba que hacen precisamente eso: menoscabar la antifragilidad de los sistemas. Esta es la tragedia de la modernidad: al igual que esos padres tan sobreprotectores que rozan la neurosis, quienes más nos intentan ayudar son quienes más nos acaban perjudicando.¿Por qué ocurre esto? En primer lugar, por lo que llamo “opacidad causal”. El intercambio de información entre los componentes de un sistema complejo es mucho más intrincado de lo que muchos nos quieren hacer ver. A nuestro alrededor hay muchas más fuentes de información de las que vemos y es difícil ver la flecha que relaciona causa y consecuencia. Esta opacidad hace que la lógica habitual y una gran parte de los métodos convencionales de análisis sean inaplicables. En un sistema complejo no podemos limitarnos a aislar una sola relación causal. Es más, la lógica, por definición, excluye los matices, y dado que la verdad reside únicamente en los matices, la lógica es un instrumento inservible para hallar la verdad en las ciencias morales y políticas.En segundo lugar, la idea de que los sistemas pueden necesitar algo de estrés y agitación ha sido pasada por alto por quienes la captan en un ámbito pero no en otro. Algunas personas pueden entender una idea en un ámbito como la medicina y no reconocerla en otro como la socioeconomía.Veamos un ejemplo de la dependencia del ámbito: preguntemos a un ciudadano estadounidense si alguna agencia gubernamental debería controlar el precio de los automóviles o de los periódicos. Seguramente nos acusaría de comunistas por el simple hecho de haberlo planteado. Vale. Luego señalémosle con mucho tacto que la Reserva Federal de los Estados Unidos se dedica, precisamente, a controlar y fijar el precio de otro bien, el tipo de interés. Ron Paul, candidato a la presidencia de los Estados Unidos, fue tildado de chalado por haber propuesto que la Reserva Federal fuera abolida. Pero también le habrían llamado chalado si hubiera propuesto la creación de un organismo que controlara otros precios.En los mercados, fijar los precios, o su equivalente consistente en eliminar a los especuladores, los llamados “negociantes del ruido” —y la volatilidad moderada que provocan—, genera una ilusión de estabilidad con períodos de calma interrumpidos por grandes saltos. Puesto que los participantes no están acostumbrados a la volatilidad, tienden a atribuir la más leve variación de los precios a información privilegiada o a cambios en el estado del sistema, lo que provoca episodios de pánico. Cuando una moneda no varía nunca, el más leve de los cambios hace que la gente crea que se acerca el fin del mundo. Inyectar un poco de confusión paradójicamente estabiliza el sistema.Las variaciones también tienen una función expurgadora. Los pequeños incendios forestales eliminan periódicamente el material más inflamable, impidiendo que se acumule. Pero la prevención metódica de los incendios por seguridad hace que los incendios grandes sean mucho peores. Por razones similares, la estabilidad per se no es buena para la economía: las empresas se debilitan durante los largos períodos de prosperidad carentes de contratiempos, y las vulnerabilidades ocultas se acumulan en silencio bajo la superficie.No forma parte de la manera aceptada de pensar que el éxito, el crecimiento económico o la innovación solo puedan surgir de una “sobrecompensación” ante ciertos estresores. Esta dificultad para traducir o extrapolar es inherente al ser humano; y solo podremos aspirar a la sabiduría y a la racionalidad si ponemos empeño en superarla.En la mitología griega, Procusto era un posadero que, para hacer que los viajeros cupieran en su lecho, estiraba hasta descoyuntarlos a los demasiado bajos y cortaba las piernas de los excesivamente altos. Así lograba que todos encajaran en la cama. Estamos fragilizando sistemas sociales y económicos negándoles estresores y azar, colocándolos en el lecho de Procusto de esta modernidad tan fácil y cómoda, pero a fin de cuentas perjudicial.
Lo antifrágil reacciona frente a los contratiempos
Creo que la innovación y la sofisticación surgen de una situación inicial de necesidad a la que se responde con algo que va mucho más allá de satisfacer esa necesidad (por ejemplo, efectos no buscados de un invento). Naturalmente, hay muchos dichos sobre esta cuestión como el que reza: “El hambre agudiza el ingenio”. Podríamos decir que lo que innova es el exceso de energía que se libera al sobrerreaccionar a un contratiempo.Esta idea contradice los métodos actuales para innovar que nos hacen pensar que la innovación es producto de la financiación burocrática, de la planificación, de colocar a la gente en una clase de la Harvard Business School impartida por un Muy Condecorado Profesor de Innovación (que nunca ha innovado en nada) o de contratar a algún consultor (que tampoco ha innovado en nada). Pero es una falacia: bastaría con pensar en los muchos empresarios sin formación que han contribuido de una manera desproporcionada a diversos avances tecnológicos desde la Revolución Industrial hasta la aparición de Silicon Valley.Sin embargo, a pesar de la visibilidad de esta contraprueba y de la sabiduría que podemos adquirir de manera totalmente gratuita de los antiguos (o de las abuelas), los “modernos” intentan innovar partiendo de una situación de comodidad, seguridad y previsibilidad en lugar de aceptar la noción de que la inventiva surge de la necesidad.A este respecto, es interesante observar que la automatización de los aviones ha hecho que volar sea muy fácil y cómodo para los pilotos, pero a costa de aumentar el peligro. El relajamiento de la atención de los pilotos por falta de estímulo ha provocado muchos accidentes. Parte del problema se debe a las normativas de los organismos que regulan la aviación comercial, que han obligado al sector a basarse más en la automatización. Por suerte, estos mismos organismos han acabado reconociendo el problema.Se dice que los mejores caballos pierden cuando compiten con otros más lentos y que ganan con rivales a su altura. La ausencia de un estresor y la ausencia de retos perjudica a los mejores. Como dice el poema de Baudelaire sobre el albatros, “sus alas de gigante le impiden caminar”: muchos rinden más en cálculo avanzado que en cálculo básico.Como vemos, la antifragilidad es lo que se despierta y reacciona en exceso para compensar los estresores y el daño. Ahora bien, no hay que confundir esto con mezclar ruido y señal a la hora de reaccionar. Imaginemos a una de esas personas a las que en el habla cotidiana calificamos de neuróticas. Si su negocio sufre un pequeño percance reacciona como si se hallara al borde de la quiebra. En lugar de reaccionar a las cosas, sobrerreacciona. Comparémosla con alguien imperturbable, con la capacidad de mantener la calma bajo fuego enemigo que se considera tan necesaria para llegar a ser un líder. En ocasiones, reaccionan si lo ven necesario y, a diferencia del neurótico, las raras veces que se enfadan todo el mundo lo nota y se lo toma muy en serio.Las personas ecuánimes solo reaccionan a información real y las neuróticas reaccionan principalmente al ruido. El ruido es lo que tendríamos que pasar por alto; la señal es lo que deberíamos tener en cuenta.Esta incapacidad personal o intelectual de distinguir entre ruido y señal es lo que está detrás de la intervención excesiva (e ingenua). Quienes actúan en las grandes empresas o en la política y cuentan con un complejo departamento dedicado a reunir datos sobrerreaccionan y confunden el ruido con información. Cuantos más datos miremos, más desproporcionada será la cantidad de ruido que obtengamos (en lugar de lo valioso, la señal).Y es que, en general, hay mucho ruido procedente de los medios de comunicación y su glorificación de lo anecdótico. Gracias a esto vivimos cada vez más en una realidad virtual separada del mundo real y cada vez nos damos menos cuenta. Y al ofrecernos explicaciones y teorías, los medios de comunicación nos inculcan la ilusión de que entendemos el mundo. Así, cuando los sistemas reprimidos y con hambre de desorden natural se vienen abajo —algo que les debe suceder tarde o temprano por ser frágiles— su caída nunca se atribuye a la fragilidad y se interpreta como el resultado de una mala previsión (que, según dicen, habría que “perfeccionar”). Sería muy poco inteligente atribuir el derrumbe de un puente frágil al último camión que lo ha cruzado, y aún lo sería más intentar predecir qué camión hará que se derrumbe. Pero eso es lo que sucede en demasiadas ocasiones. Lo que se debe estudiar es el sistema y su fragilidad, no los sucesos. No nos dejemos engañar: el índice de acierto en la previsión de sucesos raros importantes en ámbitos como la política o la economía no es que esté cerca de cero, es que es cero.Si prácticamente todo lo que viene de arriba fragiliza y bloquea la antifragilidad y el crecimiento, todo lo que surge desde abajo prospera con una cantidad adecuada de desorden y de estrés. El proceso mismo de descubrimiento, de innovación o de avance tecnológico depende de la manipulación o experimentación antifrágil, de asumir riesgos con audacia más que de la educación formal. A un vendedor de pistachos en el zoco de Damasco no le hace falta resolver ecuaciones generales del equilibrio para poner precio a su producto.El caso es que las cosas que se acaban implementando tienden a nacer de la práctica, no de la teoría. Pensemos en las bellas catedrales de Europa: parecen basarse en una geometría muy compleja. La simple credulidad nos haría pensar que estas hermosas obras se deben a la matemática. Pero los arquitectos (entonces llamados maestros de obras) se basaban en reglas heurísticas, métodos empíricos, herramientas y prácticamente ninguno sabía de matemáticas. Según el historiador de la ciencia medieval Guy Beaujouan, antes del siglo XIII no había más de cinco personas en toda Europa que supieran hacer una división. Ni teoremas, ni cuentos: los maestros de obras podían averiguar la resistencia de los materiales sin las ecuaciones que tenemos hoy y la mayor parte de aquellos edificios aún siguen en pie.Debe quedar claro que no estoy diciendo que las teorías o la ciencia académica no estén detrás de algunas tecnologías prácticas cuya aplicación final surge directamente de ellas. Pero hay todo un corpus de conocimientos prácticos que ha sido transmitido de maestros a aprendices. Y es que el papel del conocimiento formal está sobrevalorado precisamente por ser muy visible.
Tu fragilidad es mi antifragilidad
Los restaurantes son frágiles y compiten entre sí, pero el conjunto de los restaurantes de una localidad es antifrágil por esta misma razón. Si cada restaurante fuera robusto como unidad, y por lo tanto inmortal, el negocio global se habría estancado o debilitado y lo mejor que serviría sería un menú de bar al estilo soviético. Además, sufriría los efectos de carestías sistémicas y, de vez en cuando, caería en una crisis total y tendría que ser rescatado por el Gobierno.Todo lo que está vivo o es de naturaleza orgánica tiene una vida finita y acaba muriendo. Pero lo que muere lo hace después de dejar descendencia con un código genético que difiere en algún aspecto del de su progenitor. La naturaleza no considera que los individuos sean muy útiles cuando han agotado su capacidad de reproducción. Prefiere dejar que el juego continúe en el nivel informativo, el del código genético. Así pues, los organismos deben morir para que la naturaleza, esa naturaleza cruel, oportunista y egoísta, sea antifrágil.Hagamos el experimento mental de imaginar la situación de un organismo inmortal, sin fecha de caducidad. Para satisfacer las condiciones de la inmortalidad, los organismos deberían predecir el futuro a la perfección: menos que eso sería insuficiente. Pero al dejar que los organismos vivan y mueran y se produzcan modificaciones entre generaciones sucesivas, a la naturaleza no le hace falta predecir condiciones futuras más allá de una idea muy vaga de la dirección que se debe seguir. Cada suceso aleatorio traerá su propio antídoto en forma de variación ecológica. Es como si la naturaleza se modificara a sí misma y modificara su estrategia a cada instante.Consideremos este fenómeno desde el punto de vista de la vida económica. Si la naturaleza gobernara la economía, no rescataría constantemente a sus miembros para que vivieran eternamente. Ni tendría administraciones permanentes ni departamentos de previsión que intentaran adelantarse al futuro. No dejaría que los timadores de la Oficina de Administración y Presupuesto de los Estados Unidos cometieran tales errores de arrogancia epistémica.Ya hemos visto que en el contexto adecuado los estresores son información. Para lo antifrágil, el perjuicio causado por los errores debería ser menor que el beneficio. Naturalmente, me refiero a algunos errores, no a todos: los que no destruyen un sistema ayudan a impedir males mayores. Si el Titanic no hubiera naufragado y el coste en vidas no hubiera sido tan grande, se habrían construido transatlánticos cada vez más grandes y el siguiente naufragio habría sido aún más trágico. Este ejemplo ilustra la diferencia entre los beneficios para el sistema y los perjuicios para algunos de sus componentes individuales.Cada accidente aéreo nos acerca más a la seguridad, mejora el sistema y hace que el siguiente vuelo sea más seguro. Pero los sistemas de esta clase aprenden porque son antifrágiles y explotan los errores “pequeños”; no se puede decir lo mismo de las grandes crisis económicas porque el sistema económico no es antifrágil tal como está organizado hoy. La razón es que cada año hay centenares de miles de vuelos de pasajeros y el accidente de uno no repercute en los demás: los errores son localizados; en cambio, los sistemas económicos globalizados actúan como uno solo y los errores se propagan agravándose cada vez más.Para que la economía sea antifrágil y experimente lo que llamamos evolución, cada empresa por separado tiene que ser necesariamente frágil, estar expuesta a quebrar; y es que, para mejorar, la evolución necesita que los organismos (o sus genes) mueran para ser sustituidos por otros más aptos o que los menos aptos no se reproduzcan. En consecuencia, la antifragilidad de un nivel puede exigir la fragilidad —y el sacrificio— de un nivel inferior. Cada vez que preparamos nuestro café matutino con una cafetera, nos beneficiamos del fracaso —y la fragilidad— del empresario que no ha logrado que tengamos una cafetera mejor en la encimera.Es desagradable pensar que la crueldad sea un motor de la mejora. Pero hay maneras de mitigar el perjuicio para los más débiles. La solución es crear un sistema en el que la caída de uno no pueda arrastrar a otros porque los fracasos continuos actúan para mantener el sistema. Paradójicamente, muchas políticas sociales e intervenciones de los gobiernos acaban perjudicando a los débiles y consolidando a los ya establecidos.Para progresar, la sociedad moderna debería tratar a los empresarios arruinados de la misma forma que la humanidad ha venido honrando a los soldados muertos. Y es que del mismo modo que no hay soldados fracasados con independencia de que estén muertos o vivos (salvo que hayan dado muestras de cobardía), tampoco hay empresarios o investigadores científicos fracasados.
Lo antifrágil se puede enfrentar a los Cisnes Negros
Es mucho más fácil saber si algo es frágil que predecir un suceso que lo pueda dañar. La fragilidad se puede medir, pero el riesgo no (salvo en los casinos y en la cabeza de quienes se proclaman “expertos en riesgos”). Esto ofrece una solución a lo que he llamado el problema de los Cisnes Negros: la imposibilidad de calcular los riesgos de sucesos raros y de gran trascendencia y de predecir su incidencia.Los Cisnes Negros son sucesos a gran escala, imprevisibles, irregulares y con unas consecuencias de muy gran alcance que sorprenden y perjudican a ciertos observadores que no los han previsto y a los que llamaremos “pavos”. Un carnicero alimenta durante mil días a un pavo. El pavo es feliz. Y entonces llega el día de Acción de Gracias y ser un pavo ya no es muy buena idea… El día de Acción de Gracias será un suceso de Cisne Negro pero solo para el pavo, no para el carnicero. La historia del pavo también nos revela a la madre de todos los errores perjudiciales: confundir la ausencia de prueba (de un perjuicio) con la prueba de ausencia, un error que, como veremos, es bastante común.Nos dedicamos a refinar nuestra comprensión de lo ordinario creando modelos y teorías que no sirven para contemplar esos sucesos ni medir la posibilidad de que se den. Por ejemplo, los profesionales de la gestión de riesgos buscan en el pasado información sobre el llamado peor escenario y la emplean para calcular riesgos futuros: este método se llama “prueba de estrés”. Toman la peor recesión histórica, la peor guerra o los peores índices de desempleo como referencia para calcular el peor resultado futuro. Pero nunca se dan cuenta de esta incongruencia: cuando ese peor escenario del pasado sucedió, superó al “peor escenario” de su época. He llamado problema de Lucrecio a este fallo mental en honor al filósofo y poeta latino que escribió que el tonto cree que la montaña más alta del mundo es la más alta que ha visto él.Lo mismo sucedió con el reactor nuclear de Fukushima, que sufrió un fallo catastrófico en 2011 a consecuencia de un tsunami. Había sido construido para resistir el peor terremoto histórico y los constructores no imaginaron que pudiera ocurrir otro peor. Del mismo modo, en su disculpa ante el Congreso estadounidense, el expresidente de la Reserva Federal de los Estados Unidos, el fragilista doctor Alan Greenspan, ofreció el clásico “Nunca había pasado algo así”. Pues bien, la naturaleza, a diferencia del fragilista Greenspan, se prepara para lo que no ha sucedido antes presuponiendo que puede ocurrir algo peor.Los Cisnes Negros nos hacen creer que “casi” los hemos previsto porque los podemos explicar retrospectivamente cuando ya han pasado. La ilusión de que los podemos prever impide que nos demos cuenta de su papel en la vida. La vida es más —muchísimo más— laberíntica de lo que aparece en nuestra memoria: la mente convierte la historia en algo uniforme y lineal y hace que subestimemos el azar.Si sabemos en qué lado estamos de la tríada, es decir, si somos frágiles, robustos o antifrágiles, podemos determinar más fácilmente nuestra sensibilidad al daño causado por la volatilidad en lugar de rompernos la cabeza tratando de prever el suceso raro (Cisne Negro) que nos puede causar un daño irreparable.Nuestra misión en la vida (y la de cualquier sistema complejo que se precie) pasa a ser, simplemente, la de no pensar como el pavo o, si es posible, la de ser todo lo contrario, es decir, antifrágiles. Pero para no ser como nuestro querido pavo debemos empezar entendiendo la diferencia entre la estabilidad verdadera y la artificial.Consideremos la suerte que han corrido los hermanos John y George. John lleva veinticinco años de administrativo en el departamento de personal de un gran banco. George es taxista.John tiene un sueldo totalmente previsible (o eso cree), además de seguro médico y cuatro semanas de vacaciones al año. Suele despertarse diciéndose a sí mismo que “la vida va bien”. Pero eso era antes de que estallara la crisis bancaria y se diera cuenta de que su trabajo pasaría a ser “redundante”. Estar en el paro le afectaría muchísimo ya que tiene más de cincuenta años.George tiene días buenos en los que puede ganar un buen dinero; otros son peores y apenas cubre gastos; pero viene a ganar más o menos lo mismo que su hermano. Dada la variabilidad de sus ingresos, siempre se queja de no gozar de la seguridad laboral de su hermano; pero, en el fondo, este anhelo es una ilusión porque acabará mejor parado que él.Y es que esta es la ilusión fundamental de la vida: la ilusión que nos dice que la aleatoriedad es peligrosa, que es mala, y que hay que eliminarla. Los trabajadores por cuenta propia tienen unos ingresos con cierta volatilidad pero son bastante robustos frente a un Cisne Negro de poca importancia que pueda dejarlos sin ingresos. Sus riesgos son muy claros. Pero no pasa lo mismo con los asalariados: no tienen volatilidad y se ven sorprendidos cuando sus ingresos se quedan en nada tras ser despedidos. Sus riesgos están ocultos.Gracias a la variabilidad, los profesionales autónomos tienen un poco de antifragilidad: las variaciones pequeñas hacen que se adapten y aprendan del entorno, porque en cierto modo se hallan bajo una presión continua para hacerlo. Recordemos que los estresores son información; estos profesionales afrontan continuamente esos estresores y se amoldan de una manera oportunista.Así pues, y lamentablemente, a los seres humanos nos da tanto miedo la segunda forma de variabilidad que de una manera ingenua fragilizamos los sistemas —o impedimos que sean antifrágiles— protegiéndolos. En otras palabras, evitar los errores pequeños hace que los grandes sean más graves. Cuanta más variabilidad observamos en un sistema, menos propenso es a los Cisnes Negros.Y es que la antifragilidad es el mejor antídoto contra los Cisnes Negros. Olvídese de los “científicos” que se dedican a predecir lo impredecible.
El método de la haltera
Vamos a describir una estrategia para lograr antifragilidad, es decir, para pasar al lado derecho de la tríada. El primer paso para llegar a la antifragilidad consiste en reducir lo desfavorable antes de aumentar lo favorable; por decirlo de otro modo, consiste en reducir la exposición a Cisnes Negros negativos y dejar que la antifragilidad natural actúe por sí sola.Puede que sea evidente, pero se suele pasar por alto: reducir la fragilidad es un requisito, no una opción. Y es que la fragilidad es extenuante, igual que una enfermedad terminal. Si un paquete se rompe en condiciones adversas no se va a arreglar por sí solo cuando las condiciones vuelvan a ser adecuadas.Los hombres de negocios suelen pasar por alto la importancia de abordar la fragilidad primero de todo porque tienden a creer que su principal misión es generar beneficios. No ven que la supervivencia es más prioritaria que el éxito. Antes que obtener beneficios y comprarse un BMW, sería buena idea sobrevivir. En otras palabras, si algo es frágil, la amenaza de que se rompa implica que todo lo que hagamos para mejorarlo o hacerlo “eficiente” será inútil si antes no reducimos el riesgo de rotura.Es lo mismo que pasa con el crecimiento del PIB (producto interior bruto). Se puede lograr con toda facilidad endeudando a las generaciones venideras y permitiendo que la economía del futuro se pueda venir abajo por la necesidad de saldar esa deuda. Del mismo modo que la noción de “velocidad” es irrelevante para un avión que presenta un riesgo elevado de estrellarse porque sabemos que puede no llegar a su destino, al crecimiento económico con fragilidades no se le debe llamar crecimiento, algo que los gobiernos aún no han entendido. En la época dorada de la Revolución Industrial el crecimiento fue muy modesto, inferior al 1 %. Pero, aun siendo tan bajo, fue un crecimiento robusto, no como la carrera insensata de tantos Estados actuales que, en su intento de crecer, se comportan como conductores adolescentes borrachos de velocidad.¿En qué consiste la estrategia de la haltera? El objetivo de la haltera (la barra con pesas que utilizan los halterófilos) es ilustrar la idea de combinar dos extremos que se mantienen separados evitando el centro o punto medio. Con una haltera podemos adoptar la doble actitud de ir a lo seguro en algunas áreas (robusto ante los Cisnes Negros negativos) y de asumir muchos riesgos pequeños en otras (abierto a los Cisnes Negros positivos) con el fin de lograr antifragilidad.Veamos un ejemplo de haltera en el campo de las finanzas: si guardamos el 90 % de nuestros fondos en efectivo (siempre que estemos a salvo de la inflación) e invertimos el 10 % restante en valores de mucho riesgo, por un lado es imposible que perdamos más del 10% y por el otro podemos obtener pingües beneficios. Alguien que invierta el 100 % en los llamados valores de riesgo “medio” se expone a la ruina total por un mal cálculo de los riesgos. Esta estrategia de haltera soluciona el problema de que los riesgos de los sucesos raros no se puedan calcular y sean frágiles a los errores de estimación; en este ejemplo, la haltera financiera tiene una pérdida máxima conocida.La haltera evita la “media” o el “punto medio”… porque es muy peligroso. Si nos dijeran que nuestra abuela pasará las dos próximas horas a la temperatura media de veintidós grados centígrados podríamos pensar que es una temperatura ideal. Pero resulta que la abuela se pasará la primera hora a dieciocho grados bajo cero y la segunda a sesenta sobre cero con una media equivalente a veintidós grados. Así que lo más seguro es que nos quedemos sin abuela. Como vemos, la noción de media carece de importancia cuando uno es frágil a las variaciones.Las estrategias de haltera pueden ser muy variadas. El único límite es la imaginación y las circunstancias de cada persona. A modo de ilustración pensemos en la estrategia de haltera de algunos escritores. La literatura es una de las carreras más inflexibles, más especulativas, más exigente y con más riesgo. Entre los escritores existe la tradición de buscarse una profesión libre de ansiedad, con pocas exigencias intelectuales y gran seguridad laboral, la clase de trabajo que permite dedicar el tiempo libre a escribir lo que uno quiere.En política social, una haltera consistiría en proteger a los más débiles y dejar que los fuertes cumplan con su trabajo en lugar de ayudar a consolidar los privilegios de la clase media, lo que bloquea la evolución y genera toda clase de problemas económicos que tienden a perjudicar más a los más desfavorecidos.Antes de que el Reino Unido se convirtiera en un estado burocrático, presentaba una estructura de haltera formada por aventureros (tanto en lo económico como en lo físico) y por una aristocracia. No es que la aristocracia tuviera mucho peso, pero al menos ayudaba a mantener cierto sentido de precaución mientras los aventureros recorrían el planeta en busca de oportunidades de comercio o se quedaban en casa manipulando maquinaria. Hoy la City de Londres está formada por bohemios burgueses que viven de sus bonus anuales.Hay un proverbio yiddish que reza “Prepárate para lo peor, porque lo mejor se encarga de sí mismo”. Puede parecer una perogrullada, pero no lo es. Tenemos pruebas más que suficientes de que a la gente le disgustan las pérdidas pequeñas pero no tanto los grandes riesgos tipo Cisne Negro (a los que infravaloran) porque tienden a asegurarse contra pérdidas pequeñas probables, pero no contra pérdidas grandes e infrecuentes. Precisamente lo contrario de lo que deberían hacer.La haltera es una domesticación —que no eliminación— de la incertidumbre.
La estrategia de las opciones
Tales fue un filósofo jónico de linaje fenicio, que vivía en la ciudad de Mileto. Cansado de que sus amigos de espíritu más comercial le repitieran que “el que puede actuar actúa, y el que no, filosofa”, llevó a cabo una proeza: compró a muy bajo precio el derecho a utilizar hasta final de temporada todas las prensas de aceite de los alrededores de Mileto y de Quíos. La cosecha de aceitunas fue tan abundante y hubo tal demanda de prensas que las acabó arrendando a sus dueños con sus propias condiciones y amasó una fortuna considerable. Luego, se dedicó otra vez a filosofar.En esta opción, Tales tenía el derecho —que no la obligación— de usar las prensas en el caso de que hubiera una gran demanda y la otra parte tenía la obligación —no el derecho— de cedérselas. Tales pagó muy poco por aquel privilegio que le suponía unas pérdidas muy limitadas y un beneficio potencial muy grande. Aquella fue la primera opción de la que se tiene constancia.La opción es un agente de la antifragilidad (si nos permite ganar más de lo que podemos perder). En las finanzas, las opciones pueden ser caras, porque la gente sabe que son opciones y que alguien las vende y cobra por ellas, pero las alternativas más interesantes son gratuitas o, en el peor de los casos, baratas.Por ejemplo, supongamos que vivimos de alquiler con un contrato indefinido. Tenemos la opción de seguir en el piso el tiempo que queramos, no la obligación de hacerlo. Si un día nos da por mudarnos, basta con que se lo notifiquemos al dueño y adiós. Por otro lado, el dueño está obligado a dejar que sigamos viviendo en el piso pagando un alquiler previsible. Si los alquileres aumentaran mucho y en el mercado inmobiliario se creara una burbuja que acabara estallando, estaríamos protegidos. Por otro lado, si el precio de los alquileres se desplomara, podríamos cambiar fácilmente de piso y reducir los gastos mensuales. La bajada de los alquileres nos beneficia y la subida no nos perjudica. En cierto modo, la incertidumbre aumenta el valor de este privilegio. Y es que, cuanto mayor es la incertidumbre, más valiosa es una opción.Consideremos ahora la llamada “investigación blue sky” donde se destinan fondos a personas en lugar de a proyectos, y se asignan pequeñas cantidades a muchos investigadores. Estos inversores tienden a financiar emprendedores, no ideas. Como dicen ellos mismos, apuestan por el jockey, no por el caballo. El saldo o resultado final de una inversión de capital riesgo tiene una distribución estadística, sigue una ley de potencias con unas ventajas grandes, casi ilimitadas y, a causa de la opcionalidad, con unos inconvenientes limitados. Como me dijo un inversor de capital riesgo, “los beneficios pueden ser tan grandes que no te puedes permitir no estar en todo”. Una propiedad de la opción es que no le preocupa el resultado medio: solo le interesan los resultados favorables (puesto que los negativos no cuentan más allá de un punto dado).Si alguien tiene opcionalidad no hace falta que posea inteligencia, perspicacia, o aptitudes. Y es que no es necesario que acierte tantas veces. Lo único que necesita es tener la prudencia de no hacer tonterías que le perjudiquen (algunos actos por omisión) y reconocer los resultados favorables cuando se den.La opcionalidad es una forma alternativa de hacer cosas de una manera oportunista, y con la gran ventaja de que surge de una asimetría con beneficios grandes y perjuicios leves. Es un modo de domesticar la incertidumbre, de obrar de una manera racional sin necesidad de entender (o “adivinar”) el futuro. Cuanto mayor sea la incertidumbre, más importante será el papel de la opcionalidad y mejor nos irán las cosas. Esta propiedad es fundamental para la vida.
El problema de la eficiencia, el tamaño y la fragilidad
Un sábado por la tarde me acerqué hasta Nueva York en automóvil. Salí con tiempo de sobra (soy un defensor a ultranza de que la gente ponga redundancia en todos los ámbitos de su vida), pero según me iba acercando al centro me encontré en medio de un atasco monumental. Las autoridades de la ciudad habían dado permiso a una productora para rodar en el puente de la calle 59 bloqueando un carril; creyeron que, al ser sábado, no habría ningún problema. Pero aquel pequeño problema de tráfico se convirtió en un caos total a causa de los efectos multiplicativos. Este caso ejemplifica el problema fundamental de la eficiencia: una modificación pequeña da unos resultados que se acumulan en un sistema muy ajustado y que, por lo tanto, es frágil. Hay gente que pasa por alto que el funcionamiento sin problemas en unas circunstancias normales es muy, pero que muy diferente al funcionamiento en momentos de estrés. El cuello de botella de la “eficiencia demasiado eficiente” es la madre de todas las fragilidades.Pero no solo la eficiencia causa fragilidad; también el tamaño de los sistemas. El 21 de enero de 2008, el prestigioso banco parisino Société Générale se apresuró a vender en el mercado unos setenta mil millones de dólares en acciones. Los mercados no estaban muy activos porque era festivo en Estados Unidos, pero las bolsas de todo el mundo cayeron en picado cerca de un 10 %, lo que le costó cerca de seis mil millones de dólares en pérdidas solo por esta liquidación. Lo que sucedió es que habían descubierto un desfalco. Jéróme Kerviel, un administrador de operaciones financieras del banco, había estado apostando unas sumas enormes en el mercado y había ocultado estas exposiciones. Así que no les quedó más opción que vender de inmediato esas acciones que no sabían que poseían.Una liquidación de setenta mil millones de dólares en acciones supone una pérdida de seis mil millones. Pero una liquidación por valor de una décima parte, siete mil millones, no generaría ninguna pérdida porque los mercados absorberían esta cantidad sin caer en el pánico y hasta puede que no se dieran ni cuenta. Dicho de otro modo, si en lugar de un banco muy grande tuviéramos diez bancos más pequeños cada uno con su Micromonsieur Kerviel proporcional realizando estas operaciones fraudulentas al azar, las pérdidas totales para los diez bancos serían prácticamente nulas.Los análisis a posteriori fueron claramente erróneos porque atribuyeron el desastre a los malos controles del malvado sistema capitalista, y a la falta de vigilancia por parte del banco. Pero no había sido así. Tampoco fue un caso de “codicia”, como solemos pensar. El problema se debió básicamente al tamaño y a la fragilidad que conlleva.La historia de Kerviel es muy ilustrativa y la podemos generalizar a otros ámbitos. En el campo de la gestión de proyectos, Bent Flyvbjerg ha presentado pruebas sólidas de que un aumento en el tamaño de los proyectos se plasma en retrasos y en unos costes cada vez más elevados. Pero hay un matiz: hay proyectos que se pueden dividir en partes, pero otros no. Por ejemplo, los proyectos para construir puentes suponen una planificación monolítica porque no se pueden descomponer en partes más pequeñas. En el caso de las carreteras, que se construyen por tramos pequeños, el efecto del tamaño no suele ser muy grave, porque los responsables del proyecto solo cometen errores leves y se pueden adaptar a ellos.Antes se pensaba que esta subestimación de los costes de los proyectos se debía a un sesgo psicológico, a un exceso de confianza (optimismo). Pero el gran misterio es que esta subestimación parecía no existir hasta hace aproximadamente un siglo, aunque los seres humanos eran como ahora y tenían los mismos sesgos. Pensemos en el Crystal Palace de Londres, construido para la Exposición Universal de 1851. Entre la concepción del palacio y su inauguración solo pasaron nueve meses. El edificio era como un invernadero inmenso; se construyó a base de bastidores de hierro colado y de cristal fabricados casi exclusivamente en Birmingham y Smethwick.Para diseñar el proyecto no se usaron ordenadores, las piezas no se montaron lejos de su origen y en la cadena de producción participaron pocas empresas. En aquella época tampoco existían escuelas de empresariales que enseñaran algo llamado “gestión de proyectos” y fomentaran el exceso de confianza. Tampoco había empresas de consultoría. El problema de la agencia (la divergencia entre el interés del agente y el de su cliente) no era significativo. En otras palabras, era una economía mucho menos compleja que la de hoy.Los efectos de Cisne Negro van necesariamente en aumento como resultado de la complejidad, la interdependencia entre las partes, la globalización y la maldita “eficiencia” que hace que la gente se la juegue demasiado. Añadamos a eso los asesores y las escuelas de empresariales. Un solo problema en algún punto puede paralizar todo un proyecto, y los proyectos tienden a ser tan débiles como el eslabón más débil de la cadena. El mundo es cada vez menos previsible y nos basamos más y más en tecnologías que tienen errores y en interacciones que son difíciles de calcular y aún más de predecir.Y si pensamos en los gobiernos es fácil entender por qué nos meten en problemas con el dichoso déficit público: su infravaloración de los costes de los proyectos es crónica y al final terminan gastando más de lo que nos dicen. Esto me ha llevado a formular una regla de oro para todo gobierno: prohibido endeudarse, equilibrio fiscal obligatorio.
Menos es más (antifrágil)
La idea de que, en la toma de decisiones, “menos es más” significa que los métodos más simples de predicción e inferencia pueden funcionar mucho (pero mucho) mejor que otros de mayor complicación. La idea es contar con estrategias heurísticas “rápidas y frugales” con las que tomar buenas decisiones aunque el tiempo, el conocimiento y la capacidad de cálculo sean limitados.Un ejemplo de regla sencilla: hay ámbitos en los que el suceso raro (bueno o malo) tiene un efecto desproporcionado que normalmente somos incapaces de ver, por lo que si nos centramos en el aprovechamiento de (o en la protección frente a) un suceso raro de ese tipo, produciremos un cambio más que considerable en nuestra exposición al riesgo. Preocupémonos simplemente por nuestra exposición a los Cisnes Negros y la vida será más sencilla.Algunas personas están familiarizadas con la “regla del 80-20”, basada en el descubrimiento que hizo Vilfredo Pareto hace más de medio siglo de que el 20 % de la población de Italia era propietaria del 80 % de la tierra. Sin embargo, pocas son las personas conscientes de que nos estamos desplazando hacia una distribución mucho más desigual, de un “99-1”, en muchos ámbitos: un 99 % del tráfico de internet es atribuible a menos del 1 % de los sitios web; un 99 % de las ventas de libros corresponden a menos del 1 % de los autores… Casi todo lo contemporáneo tiene efectos de “el ganador se lo lleva todo”, y ahí están incluidas fuentes tanto de daños como de beneficios. Como consecuencia, con un 1 % de modificación de los sistemas puede reducirse la fragilidad (o incrementarse la antifragilidad) aproximadamente en un 99 %, y lo único que se necesita para ello son unos pocos pasos, muy pocos, y con bajo coste por lo general, para hacer que las cosas sean mejores y más seguras.Sin embargo, la gente se empeña en tener más datos para “solucionar problemas”. Tener más datos, como prestar atención al color de los ojos de las personas que nos rodean cuando estamos cruzando una calle, por ejemplo, puede impedirnos ver el camión enorme que se nos viene encima. Tal como Paul Valéry escribió en una ocasión, “cuántas cosas hay que ignorar para actuar”.
Conclusión
Cuando ha tenido lugar un suceso, en lugar de echar la culpa a la incapacidad de haberlo visto venir habría que culpar a la incapacidad de entender la (anti)fragilidad; dicho de otro modo, deberíamos preguntarnos por qué hemos construido algo tan frágil a sucesos de esta clase. No prever un tsunami o una crisis económica es excusable; construir algo que sea frágil a ellos no lo es. Podemos ver una idea similar en las palabras (quizá apócrifas) de Warren Buffett cuando dijo que intenta invertir en negocios que sean “tan buenos que hasta los pueda dirigir un idiota; porque, tarde o temprano, alguno lo hará”.Pero no tendríamos una visión completa de la tríada si no abordáramos la cuestión de la ética. Y es que hay personas que, parapetadas tras la opacidad y la complejidad de nuestro mundo, tratan de ocultar riesgos y perjudicar a otras sin que la ley ni la justicia sean capaces de detectarlas y ponerles freno. El peor problema de la modernidad radica en la transferencia maligna de fragilidad y antifragilidad de unas partes a otras, de manera que las primeras se quedan con los beneficios y las segundas son las receptoras (inadvertidas) de los daños. Estamos ante el denominado “Problema de la agencia”. Imaginemos una situación en la que el administrador de una empresa no es el verdadero dueño de esta, por lo que sigue una estrategia que parece razonable, pero que ocultamente le beneficia y le vuelve antifrágil a expensas (en forma de fragilidad) de los verdaderos dueños o de la sociedad. Cuando ese gestor acierta, recoge abundantes beneficios; cuando se equivoca, son otros los que pagan la factura.Estas situaciones poco éticas, cuando salen a la luz, se intentan camuflar con todo tipo de argumentos espurios. Fijémonos en esas empresas “demasiado grandes para caer” que se parapetan tras el argumento de que tienen una plantilla compuesta por cientos de miles de personas a las que no pueden abandonar. Como si eso fuera una “virtud” para que grandes sociedades anónimas burocratizadas se hayan hecho con el control del Estado simplemente por el hecho de que son “grandes empleadoras” y, gracias a ello, poder extraer de este importantes ventajas a expensas de las pequeñas y medianas empresas.Pero ¿cómo resolvemos este problema? Los antiguos parece que estaban mucho más avanzados de lo que estamos hoy en día a este respecto. Los romanos, por ejemplo, consideraban que los ingenieros debían pasar un tiempo bajo el puente que acababan de construir. No se trataba de castigar a los culpables con efectos retroactivos, sino de salvar vidas proporcionando desincentivos para que quien desempeñara su profesión se abstuviera al máximo de causar daños a otros.Puede que tengamos mayor justicia social que nunca antes en la historia, pero también padecemos muchas más transferencias de opcionalidad. Cuando se trata de predicciones, las palabras de los académicos, los consultores y los periodistas pueden ser solamente eso, palabras despojadas de toda prueba de verdad. Como siempre sucede con las palabras, no siempre vencen las más correctas, sino las más cautivadoras.Si alguien conduce un autobús escolar con los ojos vendados y tiene un accidente, se enfrenta a dos posibilidades: o bien muere, o bien, si sale vivo, se verá sometido a tal cantidad de penalizaciones como para no poder conducir nunca más vehículos en los que transporte a otras personas. El problema, sin embargo, es que la mayoría de los fragilistas siguen ahí, al volante del autobús. No hay penalización prevista para los creadores de opinión, banqueros, consultores, irresponsables (y trajeados) ejecutivos de empresa, burócratas… que dañan a la sociedad. Y esa es una práctica muy negativa. Ahí está, por ejemplo, la administración Obama, que trató de combatir la crisis de 2008 nutriendo sus filas de aquellas mismas personas que, poco antes, habían conducido el autobús con una venda en los ojos. A los causantes se les premió, encima, con un ascenso.Los bancos han perdido últimamente más de lo que jamás ganaron a lo largo de su historia, pero sus directivos han cobrado miles de millones de dólares en forma de retribuciones y bonificaciones. Los contribuyentes se hacen cargo de las consecuencias negativas; los banqueros se quedan con las positivas. Y las políticas dirigidas a corregir el problema están perjudicando a personas inocentes mientras los banqueros siguen con sus vidas de lujo.Quien no vea esta transferencia de antifragilidad como un robo, ciertamente tiene un problema (o es que está en el ajo).
Fin del resumen ejecutivo
Biografía del autor
Nassim Nicholas Taleb (Amioun, Líbano, 1960) ha dedicado su vida a investigar las reglas y la lógica de la suerte, la incertidumbre, la probabilidad y el saber. Matemático empírico, a la vez que analista del comportamiento económico de los seres humanos, trabajó durante 21 años como gestor de hedge funds y trader de productos derivados. Taleb ha sido investigador y docente en diversas instituciones académicas, como la NYU’s School of Engineering o la Universidad de Massachusetts en Amherst.
Es autor de los libros ¿Existe la suerte? (Ediciones Paidós, 2009), The Bed of Procrustes (Random House, 2010), El Cisne Negro (Ediciones Paidós, 2011) y Antifrágil (Ediciones Paidós, 2013).
Fermat y Pascal padres de la probabilidad moderna
mayo 1, 2017
Fermat, Pascal y los inicios de la probabilidad moderna
Te contamos cuáles fueron los comienzos de la actual teoría de la probabilidad
Por Miguel Ángel Morales.
Desde el porcentaje de que llueva o nieve un día concreto en una zona determinada hasta la idoneidad de apostar o no según la mano de póker que llevemos, pasando por las cuotas a favor o en contra de la victoria de un cierto equipo y muchos otros fenómenos físicos o económicos. Gran parte de los datos que nos encontramos a diario en muchos ámbitos están basados en el cálculo de probabilidades.
En 1933, Andréi Kolmogórov establecía la que se conoce como concepción axiomática de probabilidad, dando rigor de esta forma a muchos de los estudios que se habían realizado con anterioridad en esta rama y comenzando así el estudio moderno de la teoría de probabilidades. Pero el estudio de la probabilidad comenzó mucho antes, y se puede decir que los precursores de esta teoría fueron Pierre de Fermat y Blaise Pascal.
Nos remontamos al siglo XVII. La teoría de números da sus primeros pasos como rama de las matemáticas gracias a Pierre de Fermat, y la geometría analítica hace su aparición en las matemáticas apoyada en los estudios del propio Fermat y de René Descartes. Al margen de todo esto, la alta sociedad francesa se entretiene con juegos de azar.
Uno de sus integrantes, Antoine Gombaud, Caballero de Méré, era un experto jugador (aparte de escritor y pensador). A pesar de su sabiduría en lo que a juegos de azar se refería, había dos que le creaban dudas, que no entendía completamente. Por ello, decidió planteárselos a Pascal.
El primero que vamos a comentar es el siguiente. Supongamos que tiramos un dado cuatro veces y pensemos en la probabilidad de que salga al menos un 6 en alguna de las tiradas (da igual en cuál de ellas). La cuestión es la siguiente: ¿nos conviene apostar a que saldrá al menos un 6? Veámoslo con matemáticas.
Vamos a calcular la probabilidad de que no salga ningún 6 en ninguna de las tiradas, y el resultado se lo restaremos a 1, obteniendo así la probabilidad de que salga al menos un 6.
La probabilidad de que no salga un 6 en una tirada es 5/6 (cinco valores que no son 6 entre seis valores posibles), y como tiramos cuatro veces (y las tiradas son independientes), la probabilidad de que no salga ningún 6 en esas cuatro tiradas es:
(5/6) · (5/6) · (5/6) · (5/6) = (5/6)4
Ahora la probabilidad de que salga al menos un 6 saldrá de restar ese resultado a 1:
P(Al menos un 6) = 1-(5/6)4=0’5177…
Como nos sale un resultado mayor que 0’5, nos conviene apostar a que saldrá al menos un 6 en cuatro tiradas de un dado.
Gombaud sabía que esa apuesta era ligeramente favorable que la contraria (aunque seguro que no hizo los cálculos como hemos mostrado aquí), y a partir de aquí se planteó qué ocurriría al tirar dos dados y esperar que en ambos salga 6 al menos una vez. Su razonamiento fue algo parecido a lo siguiente:
“La probabilidad de sacar 6 en ambos dados (en una tirada) es igual a multiplicar por 1/6 la probabilidad de sacar un 6 con un dado en una tirada. Por tanto, para igualar la situación al problema anterior habría que hacer 4 · 6 = 24 tiradas. Así conseguimos un problema en el que la probabilidad de sacar 6 en ambos dados al menos una vez es la misma que la de sacar un 6 al menos una vez en el caso anterior, por lo que interesa apostar a favor de ese hecho.”
El caso es que nuestro caballero de Mére, a pesar de que aparentemente la apuesta era favorable, veía que a la larga perdía más veces que ganaba. Vamos, que la apuesta no parecía tan favorable, pero no sabía por qué. ¿Podrías ayudar tú a Antoine? Piénsalo, más adelante daremos la respuesta.
El segundo problema es, bajo mi punto de vista, más interesante. Os pongo en situación:
Imaginemos que dos jugadores A y B juegan con una moneda, tirándola y viendo lo que sale en ella. Si sale cara, A acumula un punto, y si sale cruz lo acumula el jugador B. Ambos han apostado 32 € y gana el jugador que antes llegue a 5 puntos, llevándose entonces todo el dinero (al parecer, el problema trataba de tirar un dado y cada uno había elegido un número concreto, pero para ilustrar el problema nos vale nuestro ejemplo). Por circunstancias que no vienen al caso, hay que interrumpir el juego antes de que uno de los jugadores gane, estando en ese momento el marcador así: A lleva 4 puntos y B lleva 3 puntos. La cuestión es la siguiente: ¿cómo debe repartirse el dinero?
Este problema había sido estudiado anteriormente por Luca Pacioli y por Tartaglia, pero ambos dieron respuestas erróneas. Nuestro caballero de Mére se lo propuso a Pascal, que lo puso en conocimiento de Fermat mediante correspondencia. En esa correspondencia entre estos dos monstruos de las matemáticas se resolvió este problema y, de paso, se creó el germen de la teoría del cálculo de probabilidades.
Pero vayamos al problema en sí. La primera idea, en cierto modo razonable, sería repartir el dinero total, 64 €, en proporción según los puntos que llevan cada uno de ellos en el momento en el que el juego se corta. Como en ese momento A lleva 4 puntos y B lleva 3 puntos, habría que dividir 64 entre 7 y dar 4 partes a A y 3 partes a B…
…el problema es que este razonamiento no da un resultado justo. Por ejemplo, imaginad que sólo se ha hecho una tirada y ha salido cara. Entonces A lleva un punto…y las circunstancias obligan a terminar ahí el juego. Según el razonamiento anterior, A debería llevarse todo el dinero, lo que sería a todas luces injusto.
El reparto más justo (y, por tanto, el correcto) debe ir en función de la probabilidad que tendría cada uno de ganar el juego si éste no se hubiera interrumpido. Vamos a analizar cuáles serían las probabilidades de cada uno y las usaremos después para repartir el dinero correctamente.
Como decíamos, el jugador A lleva 4 puntos y el B lleva 3 puntos, y gana el primero que llegue a 5 puntos. Si en la siguiente tirada hubiera salido una cara, el jugador A llegaría a 5 puntos y, por tanto, ganaría. La probabilidad de que ocurra eso es la probabilidad de que salga cara en una tirada: 1/2.
Si hubiese salido cruz, el jugador B sumaría 4 puntos. Como el A también lleva 4, todavía no ha ganado nadie, por lo que hay que tirar de nuevo. Si en esa segunda tirada sale cara, gana el A, y esto ocurre con probabilidad
(1/2) · (1/2) = 1/4 (el primer 1/2 por la cruz y el segundo por la última cara)
Y si en la segunda tirada sale cruz, gana el jugador B. La probabilidad de que eso ocurra es también
(1/2) · (1/2) = 1/4 (el primer 1/2 por la primera cruz y el segundo por la última cruz)
Analizando estos casos, vemos que la probabilidad de que gane A es:
P(Gana A)=1/2 + 1/4 = 3/4
Y la probabilidad de que el ganador sea B es:
P(Gana B)=1/4
Entonces debemos dividir el dinero total en cuatro partes y darle tres a A y una a B. Por tanto, al jugador A le corresponden 48 € y al B le deben dar 16 €.
Volvamos ahora al primer problema. ¿Lo has resuelto? Razonando como en el caso de una sola tirada de dado seguro que sí. Pero por si acaso vamos a comentarlo.
Vamos a calcular la probabilidad de que no salga el resultado (6,6), y después, como antes, le restaremos esa probabilidad a 1. Como el resultado (6,6) puede darse solamente en 1 de los 36 casos posibles, y tiramos el dado 24 veces, tenemos que:
P(No salga (6,6)) = (35/36)24
Ahora le restamos ese valor a 1 y obtenemos la probabilidad de que salga (6,6) al menos una vez en 24 tiradas:
P(Al menos sale (6,6) una vez en 24 tiradas) = 1 – (35/36)24 = 0’4914…
Lo que significa, al ser menor que 0’5, que apostar a ese resultado es, a la larga, perjudicial para el jugador.
Como ya hemos comentado, Pascal y Fermat comentaron y dieron solución a estos problemas en la correspondencia que se generó entre ambos (Fermat, sobre todo, era mucho de comunicarse con otros matemáticos por correspondencia) después de que el caballero de Mére se los propusiera a Pascal. Aquí tenéis traducciones al inglés de parte de esa correspondencia, aunque por desgracia no todas las cartas han llegado a nuestros días. El responsable de formalizar todos estos argumentos fue Christiaan Huygens, que tuvo conocimiento de esta correspondencia sobre 1655. En 1657 publicó el tratado De Ratiociniis in Ludo Aleae (Calculando en juegos de azar), escrito en el que resolvía los problemas sobre probabilidades que circulaban en aquella época. Este tratado se convirtió en el primero trabajo publicado sobre cálculo de probabilidades.
Como habéis podido ver, el simple planteamiento de un problema práctico por parte de Antoine Gombaud, caballero de Mére, acabó dando lugar a toda una teoría matemática con multitud de usos y aplicaciones. Y no es el único caso, recordad el caso de los puentes de Königsberg y la teoría de grafos. Por ello, no debemos restarle importancia a ninguno de los problemas que se nos puedan ocurrir o que nos puedan aparecer, ya que nunca se sabe la importancia que pueden llegar a tener o las aplicaciones que se les puede encontrar.
Fuente: elpais.com
Vincúlese a nuestras Redes Sociales:
Google+ LinkedIn YouTube Facebook Twitter
Más información:
Matemáticas y juegos de azar
.
.
Por qué se equivocaron las casas de apuestas con el Brexit
junio 27, 2016
Por qué se equivocaron las casas de apuestas con el ‘brexit’
Por Jon Sindreu.
Graham Sharpe, portavoz de la casa de apuestas William Hill, señala las probabilidades para el referendo británico.
.
Cuando la Liga Premier comenzó su última temporada en agosto pasado, los apostadores asignaban una probabilidad de 0,0002% a que el Leicester City se coronara campeón. Cuando el equipo levantó el trofeo y dio la vuelta olímpica al final de la temporada, unos pocos hinchas acérrimos ganaron miles de libras esterlinas, pero la mayoría de los apostadores perdieron todo su dinero.
Algo parecido ocurrió el viernes, cuando se anunció que la mayoría de los británicos había optado por abandonar la Unión Europea, lo cual dejó atónitos a los mercados. Al momento del cierre de las últimas mesas de votación, algunas casas de apuestas asignaban que las probabilidades de un voto a favor de dejar la UE, una opción conocida como brexit, eran menores de 10%.
“No puedo recordar ninguna otra ocasión en que las casas de apuestas se hubieran equivocado tanto”, dijo Christian Gattiker, estratega jefe del banco privado suizo Julius Baer Group AG.
Las probabilidades de los apostadores representan presuntamente la “sabiduría de las multitudes” y toman en cuenta una gama más amplia de factores que una simple encuesta, que refleja el momento en que fue hecha. Pero lejos de ser predictores puramente racionales, las probabilidades de los apostadores están sujetas a una serie de sesgos, dicen los observadores.
En principio, la mayor parte de las apuestas se estaban realizando en Londres, donde cerca de dos tercios de la población se pronunció a favor de la permanencia en la UE.
Los inversionistas también podrían haber sido víctimas de sus propios prejuicios. La comunidad británica de inversionistas locales e internacionales reside casi exclusivamente en Londres y en Edimburgo, que también votó a favor de seguir en la UE por un margen de casi tres a uno.
En la casa de apuestas londinense William Hill PLC, cuando todavía faltaban unos dos meses para la votación de la semana pasada, una mujer que dijo ser de la zona central de Londres colocó una apuesta de 100.000 libras (US$136.500) a un triunfo de la opción de permanecer en la UE, lo que le daba la posibilidad de obtener una ganancia de 40.000 libras esterlinas.
La suya fue la mayor apuesta hecha en William Hill, dice Graham Sharpe, portavoz de la compañía.
En cambio, la mayor apuesta por una votación de dejar la UE hecha con William Hill fue de apenas 10.000 libras esterlinas. La apuesta la realizaron tres personas, dos de ellas desde Londres. “Todas las grandes apuestas se hicieron en Londres, pero eso no es inusual”, manifestó Sharpe.
La casa de apuestas londinense Paddy Power, parte de Betfair Group PLC, dijo que sus probabilidades se inclinaron a favor la alternativa de quedarse debido a las grandes apuestas. Alex Donohue, vocera de la empresa de apuestas Ladbrokes PLC, indicó que cerca del 80% de las apuestas colocadas fuera de Londres fueron a favor de salir de la UE.
Ambas casas de apuestas asignaban, en la víspera de la votación, una probabilidad de 10% o menos al brexit.
El lunes pasado, Betfair tenía una probabilidad una votación a favor de abandonar la UE de cerca de 25%, una caída frente al 40% de dos semanas atrás. El jueves en la noche, el día del referendo, Betfair asignaba una probabilidad de 94% al triunfo de la opción de permanencia y la libra esterlina alcanzó su mayor nivel del año frente al dólar.
“La cotización parecía moverse al ritmo de las probabilidades que asignaban las casas de apuestas”, dijo Ben Inker, codirector de asignación de activos de la firma de gestión de fondos GMO.
Bon Browne, director de inversión de Northern Trust Corp. , manifestó que el portafolio de múltiples activos de la firma, de más de US$10.000 millones, registró una caída de 2,8% el viernes, pero agregó que el resultado no fue tan negativo tomando en cuenta las pérdidas en los mercados globales. La mayoría de las pérdidas fueron provocadas por la exposición a las acciones internacionales, las cuales hundieron 8% al portafolio, y la exposición a bonos estadounidenses de alto riesgo, explicó. De todos modos, el equipo de Northern Trust no esperaba la victoria de la opción de dejar la UE.
“Todos estaban trabajando con la misma información que estaba distorsionada y altamente correlacionada con sus propios sesgos” aseveró. Pero “hay una diferencia entre apostar e invertir”.
Muchos inversionistas tenían convicciones arraigadas de cara a la votación de la semana pasada, dijo Browne, pero lo importante era preguntar “¿es un punto de vista bien informado?”, puntualizó.
Naomi Totten, vocera de Betfair, dijo que “este mercado del referendo fue tan extraordinario como el resultado mismo”.
El viernes, no obstante, las casas de apuestas ya habían dejado atrás el brexit y estaban asignando probabilidades sobre quien será el próximo primer ministro británico.
Fuente: The Wall Street Journal, 27/06/16.
Más información:
Evolución matemática de los juegos de azar durante el siglo XIX
Matemáticas y juegos de azar
La Teoría de la Ruina del Jugador (Gambler’s Ruin)
.
Un hombre de 80 años ganó casi medio millón de dólares en una máquina tragamonedas, en el casino de Palermo (Buenos Aires)
agosto 11, 2014
Un abuelo se convirtió en millonario al ganar más de cinco millones de pesos en el casino de Palermo
Según estadísticas oficiales de la concesionaria del juego, es el pozo más grande de Sudamérica; ganó ayer en la máquina de la fortuna.
Buenos Aires — Para él la de ayer fue una tarde inolvidable. En el día del niño, la diosa de la fortuna pasó por el Hipódromo Argentino de Palermo y transformó en millonario a un abuelo: se alzó con $5.322.365 (unos 420.000 dólares al valor del mercado libre), el hasta ahora pozo más grande de Sudamérica, según información oficial de la concesionaria.
La increíble suma apareció en la pantalla de la máquina «Wheel of Fortune«, ubicada en la Tribuna Nueva del Hipódromo Argentino de Palermo, un juego con sistema de pozo progresivo en la que suele jugar este afortunado cliente de 80 años, oriundo de la localidad de Lomas de Zamora.
La que resultaba una visita más a la sala de slots del Hipódromo Argentino de Palermo, se transformó en una tarde inolvidable para este exgerente bancario. Según manifestó, compartiría su fortuna con su familia, particularmente con sus dos nietos, quienes sin duda tuvieron un día del niño inolvidable.
Fuente: LaNacion.com, 11/08/14. – 13:54 hs
[ Apuestas on line: Artículo relacionado:
Crece la industria de las apuestas en España ]
La pantalla que convirtió en rico a un abuelo. Foto: Gentileza Hipódromo de Palermo.
Evolución matemática de los juegos de azar durante el siglo XIX
junio 12, 2014
La Estadística y la Teoría de la Probabilidad en el Fortalecimiento de los Juegos de Azar:
¿Qué ocurría con la evolución de los juegos de azar durante el siglo XIX, campo primigenio en el cual había surgido la Teoría de la Probabilidad que paulatinamente se había extendido y alcanzado un desarrollo tan impresionante en todas las áreas de la ciencia?
Durante ese siglo prosperaron inicialmente los casinos que se inauguraron en los balnearios alemanes cercanos a los paisajes alpinos de la vertiente del río Rin (Wiesbaden, Baden‑Baden, Bad Homburg, Spa, Saxon‑les‑Bains, etc.), también florecieron numerosas casas de juego en el Estado de Louisiana antes de que comenzara la persecución puritana de los ciudadanos contra esa actividad pecaminosa que luego se propagó hacia otros pueblos de Estados Unidos a través del rió Mississippi, después surgieron los lujosos casinos de la Riviera Francesa como el de Monte Carlo a la cabeza del mundo por mucho tiempo, también se consolidaron los exclusivos clubes de juego para caballeros y las apuestas hípicas en el Reino Unido, florecieron los garitos y los Círculos Privados de juego en la alegre París convertida en una «ciudad‑espectáculo» después de su renovación urbanística concluida bajo el mando del Barón Haussmann, así como proliferaron los garitos en otras acogedoras ciudades francesas, y finalmente también crecieron los rústicos casinos a la americana (el famoso Saloon) durante el proceso de la colonización del Lejano Oeste.
Fundamentación matemática de los juegos de azar durante el siglo XIX.
Los flâneur del siglo XIX, es decir, los consumidores del ocio de la Modernidad, esto era todo lo que veían que ocurría ante sus ojos, pero tal vez muy pocos de ellos imaginaban que detrás de la fachada de los clubes, de las casas de juego, de las ventanillas de recepción de apuestas, de los garitos y de los casinos, el funcionamiento del negocio estaba dictado solamente por los últimos avances de la Teoría de la Probabilidad combinada con los aportes de la Estadística como herramienta de medición de los hechos inciertos o aleatorios. En efecto, en aquel tiempo los empresarios del ocio veían los juegos de azar simplemente como un «buen negocio comercial», que sólo es rentable si desde un comienzo le garantiza a la Banca la expectativa de obtener económicamente un cuantificable Valor Esperado (Expected Value) que constituye la Ventaja Matemática a su favor (House Edge), además de que tal rentabilidad sólo se puede concretar si siempre se garantiza un comportamiento impredecible del juego y si sólo se le ofrece al apostador opciones de triunfo «no equitativas» y desiguales frente a las reales opciones de triunfo de la Banca.
Estos primeros empresarios de los casinos, como los famosos hermanos Blanc que dirigieron el casino de Bad Homburg o el de Monte Carlo, eran gente que conocía del comercio, de la especulación financiera en las bolsas y en los bancos, de los criterios económicos aplicables a los negocios de alto riesgo, y por eso estas personas eran seguidoras de los últimos avances matemáticos y estadísticos ocurridos en el campo actuarial y de los seguros que eran una actividad comercial en la que el lucro se obtenía a partir de explotar las expectativas de ganancia o de pérdida en torno de la fortuita ocurrencia o no ocurrencia de ciertos siniestros (naufragios de barcos, deterioro de mercancías, incendios de fábricas, fallecimientos, robos, etc.), es decir, los empresarios de los casinos aplicaron en la administración de su negocio de los juegos de azar muchos de los criterios económicos y matemáticos que regían en el campo de los seguros que era el tipo de negocio más semejante a su actividad, y por eso ellos eran amplios conocedores de conceptos tales como la Teoría de la Ruina, la Pérdida Máxima Probable, el Cálculo del Riesgo Esperado, el Cálculo de las Reservas Disponibles, etc.
Estos primeros empresarios profesionales de los casinos para la adecuada administración de sus negocios del ocio también se asesoraban de importantes matemáticos pagándoles jugosos honorarios, y eran seguidores asiduos de las discusiones y las publicaciones sobre temáticas de probabilidad y estadística producidas por los sabios de su tiempo, por las asociaciones científicas, por las agremiaciones de contables o por los profesores de las universidades de Cambridge, Harvard, Oxford, la Sorbona, Turín, Berlín, etc. Además, tomando como referente el modelo de la Distribución Normal de la probabilidad ampliamente desarrollado por Laplace, Gauss, Poisson o Chebyshev, estos empresarios de los casinos sabían que en cualquier juego de azar, entre más jugadas se realicen, lo más probable es que las apariciones aleatorias de los resultados esperados se concentrarán dentro de ciertos límites en torno de un número ideal de apariciones, es decir, estadísticamente se prevé que los juegos de azar tienen un comportamiento más o menos regular que se puede proyectar previamente mediante el cálculo de probabilidades, comportamiento dentro del cual es poco probable que un resultado específico llegue a aparecer una cantidad excesiva de veces superior a las previstas, hasta el punto de volverse «predecible» a los ojos de los jugadores en contra de los intereses económicos de la Banca. Los empresarios que administraron los primeros grandes casinos le apostaban a la ocurrencia de esa forma de distribución de la probabilidad, le apostaban a que siempre el juego se comportaría aleatoriamente arrojando resultados que aunque en cada jugada son impredecibles, en todo caso globalmente se enmarcan dentro de unos límites más o menos previsibles desde el punto de vista estadístico, y por tanto, si en la mayoría de las ocasiones esos límites se dan, entonces se puede prever que al final la Banca siempre hará efectiva su ventaja matemática sobre los jugadores obteniendo importantes ingresos sobre todo el dinero que fue apostado por ellos.
Todo este conocimiento matemático, estadístico, contable y económico fue aplicado por los empresarios de los casinos en la creación de los nuevos juegos de azar, en la formulación de las reglas aplicables a cada juego, en el diseño de los tapetes de las mesas, en la selección precisa de las únicas opciones a las cuales les pueden apostar los jugadores, en el establecimiento de los montos de los premios que pueden ser pagados, en la fijación de los topes mínimos y máximos de las apuestas que se pueden admitir en cada mesa, etc. Se puede afirmar que, paradójicamente, desde el siglo XIX en las mesas de los juegos de azar de los casinos «nada ocurre al azar», porque los nuevos juegos de azar de la Modernidad no surgieron por generación espontánea ni por tradición cultural ni por caridad para agradarle a los consumidores del ocio, sino que surgieron como parte del engranaje de un gran negocio basado en la explotación de la ventaja matemática (House Edge) que conscientemente se establece a favor de la Banca en cada juego ofrecido al público.
En síntesis, desde el siglo XIX en una mesa de juego de un casino todo está debidamente calculado y planeado, para que desde el mismo momento en que el jugador coloque su apuesta sobre el tapete, las probabilidades y la estadística indiquen que esa apuesta muy probablemente deberá generar un flujo de rentabilidad a favor de las arcas de la Banca. Incluso la recaudación de este flujo rentable de dinero fue perfeccionada y comenzó a operar «automáticamente» gracias al ingeniero norteamericano Charles Fey, cuando basado en los diseños de las máquinas calculadoras, las cajas registradoras, los organillos de manivela, etc., inventó en 1897 la denominada «Máquina Tragamonedas» (Slot Machine), novedoso aparato que no sólo inauguró la gran época en que el comportamiento aleatorio de los juegos de azar comenzó a ser simulado mediante artilugios mecánicos, sino que además a la postre permitió que los empresarios de los casinos tuvieran una mayor seguridad acerca de la expectativa de obtener la recaudación de un porcentaje fijo de rentabilidad sobre el funcionamiento diario de tales máquinas.
Fortalecimiento de las Creencias Especulativas de los Apostadores respecto de los Juegos de Azar:
¿Qué hacían los jugadores y los apostadores del siglo XIX mientras todo lo anterior ocurría en la evolución matemática de los juegos de azar y del negocio de los casinos?
Al respecto un gran porcentaje de los jugadores posiblemente eran hábiles tahúres muy tramposos, que preferían aquellos juegos en los que tenían acceso a la manipulación directa de las cartas o de los dados, o preferían juegos en los que podían actuar en colusión con otros jugadores para así poder realizar todo tipo de timos y trampas contra los contrincantes ingenuos, únicas vías que encontraban seguras para la obtención de ganancias en los juegos de azar.
Muchos otros jugadores, fieles a la noble filosofía consumista del flâneur, consideraban impropio y poco caballeroso pensar en el dinero perdido en los juegos de azar o siquiera expresar cualquier emoción ante el anhelo de ganar una fortuna a través de ese medio: se jugaba, luego se ganaba o se perdía, pero siempre se aceptaban los resultados del azar con gallardía y caballerosidad.
Otros jugadores, menos dóciles a someterse pasivamente al imperio del azar, quizá aplicaban algunos análisis combinatorios muy simples para calcular sus expectativas de triunfo o para elegir las opciones a las que se les debía apostar.
Un creciente porcentaje de jugadores creían a pie juntillas en la falacia de la «Ley del Equilibrio Cósmico» que necesariamente se debe producir en la cantidad de apariciones de los resultados opuestos de un juego de azar entre más jugadas ocurran, falacia que desde los tiempos de D’Alembert inspiró a muchos apostadores a crear diversos sistemas de apuestas supuestamente infalibles, aplicables en mayor medida al Trente‑et‑Quarante o la ruleta, sistemas absurdos basados realmente en simples martingalas y en progresiones en el incremento o en el descenso de la cantidad apostada en cada jugada, tales como la Gran Martingala, la Pequeña Martingala, el sistema Labouchere, la Progresión de Wrangler, el sistema Philiberte, el sistema Fitzroy, el sistema Tiers et Tout, el sistema Montant Belge, el sistema Paroli, etc.
Otros más, tal vez habían escuchado que la estadística era una ciencia que trabajaba de la mano con el cálculo de probabilidades para el análisis del comportamiento de los eventos aleatorios, pero lo único que ellos en verdad sabían sobre la aplicación de la estadística era recolectar unos pocos resultados aparecidos en algún juego de azar y comenzar a apostarle a los resultados que a primera vista parecían «más dominantes» o «más salidores» en el grupo analizado, sin emplear ningún procedimiento matemático serio para verificar si esos resultados presuntamente dominantes o salidores en verdad representaban una «desviación significativa» en el comportamiento aleatorio del juego o si solamente se enmarcaban dentro de los límites previsibles del azar.
Solamente hasta 1873 se conoció de la legendaria hazaña del ingeniero inglés Joseph Hobson Jagger (1830−1892), quien al parecer usó las técnicas de muestreo, de análisis estadístico y de cálculo de probabilidades para descubrir unas fuertes tendencias en una de las ruletas del casino de Monte Carlo, descubrimiento que según se dice le permitió amasar una gran fortuna al apostarle a los números que más probabilidades tenían de aparecer. Después de esta hazaña se conoció de un grupo de jugadores italianos que hacia 1880 también aplicaron las técnicas de la estadística y del cálculo de probabilidades para amasar una gran fortuna nuevamente en las ruletas desviadas de Monte Carlo, y posteriormente durante varias décadas no se volvió a conocer ninguna noticia, anécdota, sistema o libro que hablara a profundidad, con detalles y con ejemplos prácticos, sobre la manera de aplicar de forma conjunta la Estadística y la Teoría de la Probabilidad a concretos juegos de azar para amasar fortunas.
Resulta curioso que durante el siglo XIX los empresarios que administraron los casinos usaron a plenitud todos los elementos de la Estadística y de la Teoría de la Probabilidad para perfeccionar la ventaja matemática establecida en los juegos de azar y protegerse contra el riesgo, contra la probabilidad de ruina, contra las desviaciones inusuales en la aparición de los resultados aleatorios, contra la falta de reservas económicas, etc.; mientras que la mayoría de los jugadores se quedaron estancados en el uso precario del análisis combinatorio o en la creencia en la inmutable Ley del Equilibrio Cósmico que fue defendida por D’Alembert quizá en un momento de desvarío. En otras palabras, absurdamente para enfrentarse a los juegos de azar de la Modernidad los jugadores no estaban empleando las mismas herramientas matemáticas, estadísticas y del cálculo de probabilidades que usaron los empresarios para lograr el perfeccionamiento de la ventaja matemática establecida en tales juegos.
La culpa tal vez no era de los jugadores, sino de la ausencia de fuentes de información especializadas y serias en la aplicación de la Estadística y de la Teoría de la Probabilidad a los juegos de azar. En efecto, si uno analiza las grandes obras sobre estadística y probabilidad del siglo XIX escritas por verdaderos genios matemáticos de la talla de Laplace, Gauss, Poisson, Quetelet o Chebyshev, encuentra que estos sabios para poder explicar los conceptos básicos usados en sus obras acuden inicialmente a ejemplos muy simples basados en el lanzamiento de monedas, el lanzamiento de dados, la extracción aleatoria de cartas de un mazo, la extracción aleatoria de balotas de una urna, el análisis del Problema de los Puntos, etc., pero luego estos sabios se elevan a las alturas intelectuales y se adentran en la axiomatización de los conceptos explicados ligando su aplicación a la solución de problemas más trascendentales que merecían toda su atención, tales como el desciframiento de las órbitas de los planetas, la forma como se comporta la luz, el cálculo de la trayectoria de los planetoides, el cálculo de la resistencia de los metales usados en la fabricación de las mercancías, el cálculo del grado de error cometido en una observación, el desvío esperado en el comportamiento de una variable en un experimento de laboratorio, el cálculo esperado en el crecimiento de la población, el cálculo de la ocurrencia de posibles siniestros asegurados, etc. En las obras de estos grandes autores matemáticos no hay referencias a la manera práctica de aplicar y sacar provecho del Muestreo Estadístico, la Distribución Normal, la Varianza, la Desviación Típica o los Niveles de Confianza a juegos de azar concretos como el Baccarat, el Trente‑et‑Quarante, la ruleta francesa, el Chuck‑a‑Luck, las loterías, etc.
Lo anterior no significa que durante el siglo XIX no se hayan escrito obras de literatura especializada sobre los juegos de azar, pues de hecho se escribieron muchas, mereciendo mención especial por su popularidad las siguientes:
An exposure of the arts and miseries of gambling, (1843). Escrita por Jonathan H. Green y publicada en Filadelfia.
Traité du Trente‑Quarante contenant des analyses et des faits pratiques du plus haut intéret suivis d’une collection de plus de 40.000 coups de banque, (1853). Escrita por G. Grégoire y publicada en París.
Nouveau manuel complet des jeux de calcul et de hasard ou Nouvelle Académie des Jeux, (1853). Escrita por Lasserre, Lebrun y Leroy, y publicada en París.
Routledge’s Whist Player’s Handbook, (1854). Escrita por N. Routledge y publicada en Londres.
Jeux de la Roulette et du Trente et Quarante, Méthode, (1880). Escrita por Menaldo y publicada en Niza.
Le jeu public et Monaco, (1882). Escrita por Le Docteur Prompt, y publicada en Paris.
Les grands jeux: Roulette, Trente & Quarante, Baccarat, Bourse; (1885). Escrita por Pierre Boissier y publicada en París.
Il Giuoco del Lotto, (1886). Escrita por M. de Ciutiis y publicada en Nápoles.
Une lune de miel à Monte Carlo, (1887). Escrita por Adolphe Belot y publicada en Paris.
Girotechnie ou la description scientifique de la roulette, (1890). Escrita por el doctor C. Surville y publicada en Niza.
Montecarlo occulto, Montecarlo palese, (1899). Escrita por Barone York y publicada en Turín.
Sin embargo, estas obras, y muchas otras de su mismo estilo escritas y publicadas en el siglo XIX, se dedican principalmente a explicar las reglas aplicables a populares juegos de azar como el veintiuno, el póquer, el whist, la ruleta, el Trente‑et‑Quarante, el baccarat, etc., pero no ofrecen un análisis serio de esos juegos que se fundamente en el cálculo de probabilidades o en el estudio estadístico de los resultados aleatorios. Realmente esas obras se limitan a proponerle al lector la aplicación de una serie de sistemas de colocación de apuestas, martingalas y progresiones que generalmente están basadas en las «falacias del jugador», sin ofrecer una verdadera prueba matemática de su efectividad frente a la Banca, todo lo cual es adobado además con una serie de anécdotas, especulaciones, recomendaciones y observaciones basadas sólo en la experiencia personal del autor de cada obra. En verdad es muy difícil creer que esas obras tienen un auténtico carácter científico, debido a la gran cantidad de especulaciones y suposiciones que emplean en la fundamentación de los diversos temas que tratan.
¿Por qué los grandes genios matemáticos y científicos del siglo XIX no aprovechaban sus conocimientos para escribir obras especializadas y serias sobre los juegos de azar?
Quizá muchos matemáticos, contables, ingenieros y científicos de esa época, que habían sido consultados por los mismos empresarios administradores de los casinos que perfeccionaron los modernos juegos de azar para así garantizar las ganancias de la Banca, sabían que si los juegos de azar tienen un comportamiento aleatorio que estadísticamente es próximo al modelo de la Distribución Normal, entonces no vale la pena gastar las neuronas tratando de formular sistemas matemáticos de apuestas que supuestamente prometen obtener ganancias exorbitantes en los juegos de azar, cuando realmente en muy contados casos el jugador verá ocurrir una inusitada racha favorable que se desvié significativamente más allá del comportamiento promedio del juego, lo cual tiene una probabilidad de ocurrencia siempre muy baja.
Tal vez por eso tampoco resulta extraño que desde el siglo XIX muchos jugadores hayan terminado parapetados en la lectura de obras que hablan de milagrosos sistemas de apuestas que sólo se basan en las falacias, o que, en el peor de los casos, al intentar encontrar sistemas infalibles de apuestas que puedan vencer a la Banca, hayan terminado por revivir las viejas creencias místicas sobre la «Diosa Fortuna» (el uso de talismanes, patas de conejo, fe ciega en las corazonadas, etc.) que son propias de aquella remota época pagana y oscurantista en que aún en los juegos de azar no regía la ventaja matemática perfeccionada a favor de la Banca.
Bibliografía consultada:
HALD, Anders. A history of mathematical statistics from 1750 to 1930. John Wiley & Sons, New York, 1998.
KILBY, J. y FOX, J. Casino operations management. John Wiley & Sons, New York, 2005.
KOYRE, Alexandre. Estudio de historia del pensamiento científico. Editorial Siglo XXI, Ciudad de México, 1978.
STIGLER, Stephen. The history of statistics: the measurement of uncertainty before 1900.Belknap Press/Harvard University Press, 1990.
WIKIPEDIA. Consulta de los términos: Expected Value; Gambler’s Fallacy; Gambling; History of Statistics; House Edge; Wagering Business.
Fuente: http://www.eyeintheskygroup.com, 2014.
———————–
Más información relacionada:
Juego Seguro on line en España
La industria de las apuestas continúa su escalada
